Dalam artikel ini, kita akan menghuraikan proses Ornstein-Uhlenbeck, menerangkan formula matematiknya, menerapkan dan memodelkannya menggunakan Python, dan membincangkan beberapa aplikasi praktikal dalam kewangan kuantitatif dan perdagangan sistematik. Kita akan menggunakan model proses rawak yang lebih maju, yang dikenali sebagai proses Ornstein-Uhlenbeck (OU), yang boleh digunakan untuk memodelkan urutan masa pengembalian yang menunjukkan tingkah laku kemerosotan. Ini sangat berguna untuk pemodelan kadar faedah dalam harga derivatif dan untuk menjalankan algoritma perdagangan sistematik semasa perdagangan.

Apakah proses Ornstein-Uhlenbeck?

Proses Ornstein-Uhlenbeck adalah proses kebarangkalian masa yang berterusan yang digunakan untuk memodelkan kelakuan regresi nilai rata-rata. Ini bermakna bahawa, tidak seperti standard random drift atau Brownian motion yang boleh bergerak tanpa had, proses OU cenderung untuk kembali ke nilai purata jangka panjang dari masa ke masa. Secara matematik, proses OU adalah penyelesaian kepada persamaan pembezaan rawak tertentu (SDE) yang mengawal kelakuan regresi nilai rata-rata ini.

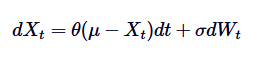
Di antaranya, Xt mewakili proses rawak pada masa t, μ adalah purata jangka panjang, θ adalah kadar pulangan purata, δ adalah turun naik, dan dWt adalah proses Wiener atau pergerakan Brown standard.

Latar belakang sejarah dan aplikasi

Proses Ornstein-Uhlenbeck pertama kali dikemukakan oleh Leonard Ornstein dan George Eugene Uhlenbeck pada tahun 1930 untuk mensimulasikan kelajuan zarah yang bergerak Brownian dalam keadaan yang bergolak. Seiring dengan berjalannya masa, kegunaannya telah melampaui fizik, dengan aplikasi dalam pelbagai bidang seperti biologi, kimia, ekonomi dan kewangan.

Dalam kewangan kuantitatif, proses OU sangat berguna untuk memodelkan fenomena yang menunjukkan tingkah laku pengembalian nilai rata-rata. Contoh yang terkenal termasuk turun naik kadar faedah, kadar pertukaran, dan pasaran kewangan. Sebagai contoh, model kadar faedah yang popular, model Vasicek, adalah model yang diturunkan secara langsung dari proses OU.

Kepentingan dalam kewangan kuantitatif

Proses Ornstein-Uhlenbeck sangat penting dalam kewangan kuantitatif kerana sifat regresi rata-ratanya menjadikannya pilihan semulajadi untuk pemodelan pembolehubah kewangan yang tidak menunjukkan pergerakan rawak, tetapi turun naik rata-rata jangka panjang yang stabil. Ciri ini penting untuk pemodelan kadar faedah, di mana regresi rata-rata mencerminkan pengaruh bank pusat terhadap kadar faedah stabil jangka panjang.

Di samping itu, proses OU juga digunakan dalam model harga aset (termasuk penilaian derivatif) dan strategi pengurusan risiko. Ia juga boleh digunakan sebagai blok bangunan model yang lebih kompleks, seperti model Cox-Ingersoll-Ross (CIR), yang memperluaskan proses OU untuk memodelkan kadar faedah yang tidak negatif.

Ciri-ciri utama dan intuisi

Ciri-ciri utama proses Ornstein-Uhlenbeck boleh diringkaskan sebagai berikut:

• Kembalikan nilai purata:Proses OU cenderung untuk kembali ke nilai purata jangka panjang μ. Ini berbeza dengan proses seperti pergerakan Brown, yang tidak menunjukkan trend ini.
• Ketidaktentuan:Parameter δ tahap keacakan atau turun naik dalam proses kawalan: semakin tinggi turun naiknya, semakin besar penyelewengan proses dari nilai purata sebelum pengembalian.
• Kelajuan kembali:Parameter θ menentukan kelajuan proses kembali ke nilai purata.
• Kestabilan:Proses OU adalah stabil, yang bermaksud bahawa ciri statistiknya tidak berubah dari masa ke masa. Ini sangat penting untuk memodelkan sistem yang stabil dalam bidang kewangan.

Secara intuitif, anda boleh menganggap proses Ornstein-Uhlenbeck sebagai pemodelan kelakuan otot cortex yang mengelilingi nilai purata. Walaupun proses itu mungkin menyimpang dari nilai purata kerana turun naik secara rawak, tali tarik otot cortex (bersama dengan kemunduran nilai purata) memastikan ia akhirnya kembali ke nilai purata.

Perbandingan dengan proses rawak lain

Oleh kerana proses OU berkaitan erat dengan pemodelan pelbagai fenomena kewangan, ia sering dibandingkan dengan proses rawak lain seperti Gerakan Brown dan Gerakan Brown Geometrik (GBM). Berbeza dengan Gerakan Brown (Gerakan Brown tidak mempunyai kecenderungan untuk kembali ke nilai rata-rata), proses OU mempunyai tingkah laku pengembalian nilai rata-rata yang jelas.

Berbanding dengan GBM yang biasanya digunakan untuk memodelkan harga saham dan mengandungi elemen hanyut dan bergelombang, proses OU tidak menunjukkan pertumbuhan indeks, tetapi bergoyang di sekitar nilai purata. GBM lebih sesuai untuk memodelkan jumlah yang meningkat dari masa ke masa, sementara proses OU sangat sesuai untuk memodelkan pembolehubah yang menunjukkan ciri-ciri pulangan nilai purata.

Contoh kewangan kuantitatif

Proses Ornstein-Uhlenbec mempunyai aplikasi yang luas dalam bidang kewangan, terutamanya dalam senario pemodelan dengan nilai purata kembali sebagai ciri-ciri utama. Di bawah ini, kami akan membincangkan beberapa kes penggunaan yang paling biasa.

Pemodelan kadar faedah

Salah satu aplikasi yang paling menonjol dari proses OU adalah pemodelan kadar faedah, terutamanya dalam rangka model Vasicek. Model Vasicek mengandaikan bahawa kadar faedah mengikuti proses OU, iaitu kadar faedah cenderung kembali ke nilai purata jangka panjang dari masa ke masa. Ciri ini sangat penting untuk mensimulasikan dengan tepat tingkah laku kadar faedah, kerana kadar faedah cenderung tidak bergelombang selama-lamanya, tetapi bergelombang di sekitar tahap purata yang dipengaruhi oleh keadaan ekonomi.

Harga aset

Dalam penilaian aset, terutamanya sekuriti pendapatan tetap, proses OU biasanya digunakan untuk mensimulasikan evolusi kadar pulangan bon. Sifat regresi nilai purata proses OU memastikan bahawa kadar pulangan tidak terlalu jauh dari nilai purata sejarahnya, yang selaras dengan tingkah laku pasaran yang diperhatikan. Ini menjadikan proses OU sebagai alat berharga untuk penetapan harga bon dan instrumen sensitif kadar faedah lain.

Strategi perdagangan pasangan

Perdagangan berpasangan adalah strategi neutral pasaran yang melibatkan penubuhan kedudukan offset di antara dua aset yang berkaitan. Dalam kes ini, proses OU sangat berguna kerana ia dapat memodelkan perbezaan harga antara dua aset, dan perbezaan harga biasanya adalah pengembalian nilai rata-rata. Dengan menggunakan proses OU untuk memodelkan perbezaan harga, peniaga dapat mengkonfirmasi masuk dan keluar keuntungan apabila harga menyimpang dari nilai rata-rata, meramalkan pengembalian nilai rata-rata, dan dengan itu menghasilkan isyarat perdagangan.

Sebagai contoh, jika perbezaan harga antara dua niaga berjangka berkembang melebihi nilai terendah, peniaga mungkin akan melakukan shorting pada niaga berjangka yang berkinerja baik dan melakukan lebih banyak niaga berjangka yang berkinerja buruk, dengan harapan perbezaan harga akan kembali ke tahap purata sejarahnya, dan dengan itu membuat keuntungan apabila pembalikan berlaku.

Penyelesaian SDE Ornstein-Uhlenbeck

Persamaan pembahagian bagi proses Ornstein-Uhlenbeck adalah asas penyelesaian SDE ini. Untuk menyelesaikan SDE ini, kita menggunakan kaedah faktor integrasi. Mari kita tulis semula SDE:

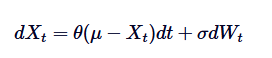
Pertama, kita perlu kalikan kedua-dua belah pihak dengan faktor integrasi /upload/asset/28dfe9abfb54772651590.png:

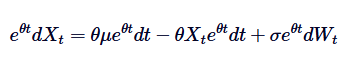
Perhatikan bahawa jika kita menambah 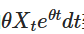di kedua-dua belah pihak, maka bahagian kiri dapat dinyatakan sebagai perbezaan perkalian:

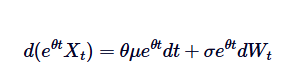
Dengan mengintegrasikan kedua-dua sisi dari 0 ke t, kita dapat:

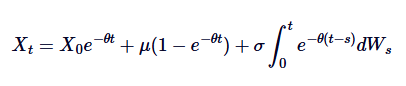
Ini adalah penerangan umum Ornstein-Uhlenbeck SDE.

Penyelesaian eksplisit yang dikemukakan di atas mempunyai beberapa makna penting. Perkara pertama 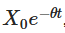menunjukkan bahawa nilai awal merosot dari masa ke masa, menunjukkan bagaimana proses itu secara beransur-ansur lupa di mana ia bermula. Perkara kedua 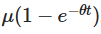menunjukkan bahawa proses itu cenderung ke nilai rata-rata μ dari masa ke masa. Perkara ketiga memperkenalkan keacakan, di mana integrasi proses yang melibatkan Wiener menjelaskan pergerakan rawak.

Penyelesaian ini menekankan keseimbangan antara kelakuan pengembalian nilai rata-rata kepastian dan faktor rawak yang didorong oleh pergerakan Brownian. Memahami penyelesaian ini adalah penting untuk mensimulasikan proses OU dengan berkesan, seperti yang dinyatakan di bawah.

Hubungan dengan proses rawak lain

Proses Ornstein-Uhlenbeck mempunyai beberapa hubungan penting dengan proses rawak terkenal lain (termasuk pergerakan Brown dan model Vasicek).

Hubungan dengan gerakan Brown

Proses Ornstein-Uhlenbeck boleh dilihat sebagai versi pengembalian rata-rata pergerakan Brown. Pergerakan Brown menggambarkan proses yang mempunyai peningkatan bebas dan tidak mempunyai trend pengembalian rata-rata, manakala proses OU menggunakan pengubahsuaian pergerakan Brown untuk memperkenalkan pengembalian rata-rata, dan dengan itu menarik proses kembali ke nilai pusat. Secara matematik, jika kita menetapkanθ = 0, proses OU akan disederhanakan kepada pergerakan Brown standard yang bergelombang:

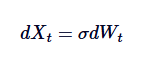
Oleh itu, pergerakan Brown adalah satu contoh khas proses OU, yang sesuai dengan kekurangan pengembalian nilai rata-rata.

Hubungan dengan model Vasicek

Model Vasicek digunakan secara meluas dalam pemodelan kadar faedah, yang pada dasarnya adalah proses Ornstein-Uhlenbeck dalam evolusi kadar faedah. Model Vasicek mengandaikan kadar faedah mengikuti proses OU, di mana SDE ditakrifkan sebagai:

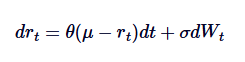
Di antaranya, rt mewakili kadar faedah jangka pendek, dan tafsiran parameterθ, μ danδ serupa dengan tafsiran dalam proses OU. Model Vasicek mampu menghasilkan laluan kadar faedah regresi rata-rata, yang merupakan salah satu kelebihan utamanya dalam pemodelan kewangan.

Memahami hubungan-hubungan ini dapat memberi pemahaman yang lebih luas mengenai bagaimana proses OU digunakan dalam pelbagai persekitaran, terutamanya dalam bidang kewangan. Kami akan membincangkan makna sebenar hubungan-hubungan ini semasa membincangkan contoh aplikasi di bawah.

Proses Ornstein-Uhlenbeck yang disimulasikan menggunakan Python

Dalam bahagian ini, kita akan membincangkan bagaimana menggunakan Python untuk mensimulasikan proses Ornstein-Uhlenbeck (OU). Ini melibatkan persamaan mikro-random yang menggunakan Euler-Maruyama dissociation untuk dissociate proses OU.

Perpecahan SDE

Mari kita lihat semula formula matematik SDE di atas dan jelaskan setiap istilah:

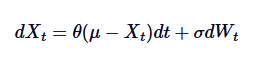
dalam,

• Xt adalah nilai proses pada masa t.
• θ ialah kelajuan pulangan nilai purata.
• μ adalah purata jangka panjang proses.
• δ adalah parameter kadar lonjakan.
• dWt mewakili peningkatan proses Wiener (pergerakan Brown standard).

Untuk mensimulasikan proses ini di komputer, kita perlu melakukan disassociation untuk SDE masa berturut-turut. Satu kaedah yang biasa digunakan adalah disassociation Euler-Maruyama, yang menghampiri proses berturut-turut dengan mengambil kira langkah masa berturut-turut yang kecil.

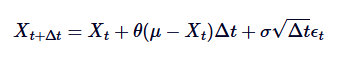
Di antaranya, 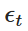adalah pembolehubah rawak yang diambil dari sebaran normal standard (iaitu 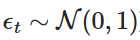). Disassociasi ini membolehkan kita mengulangi nilai Xt dari masa ke masa, dan dengan itu meniru tingkah laku proses OU.

Penerapan Python

Sekarang mari kita amalkan Ornstein-Uhlenbeck Process yang terpencil dengan Python. Dalam konteks ini, kita hanya menggunakan NumPy dan Matplotlib Python Library.

Pertama, kita mengimpor NumPy dan Matplotlib dengan cara standard. Kemudian, kita menetapkan semua parameter untuk model OU. Kemudian, kita terlebih dahulu menetapkan array NumPy dengan panjang N, untuk menambahnya setelah mengira laluan OU. Kemudian kita mengulangi langkah N-1 (langkah 1 adalah syarat awal yang ditetapkan X0), mensimulasikan peningkatan rawak DW, dan kemudian mengira iterasi seterusnya laluan OU berdasarkan formula matematik di atas.

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 10.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

Hasilnya adalah seperti berikut:

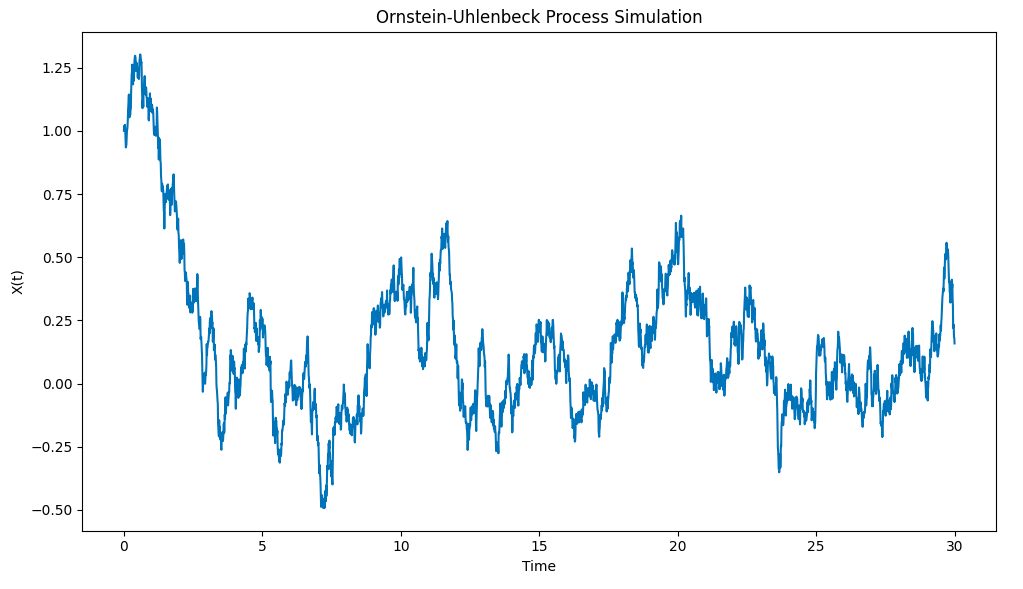
Simulasi proses Ornstein-Uhlenbeck yang dilukis menggunakan Python

Perhatikan bagaimana proses ini dengan cepat mengepam titanium X0 = 1 dari keadaan awal ke nilai purata μ = 0, dan kemudian apabila ia menyimpang dari nilai purata itu, ia menunjukkan kecenderungan untuk kembali ke nilai purata itu.

Ringkasan dan langkah seterusnya

Dalam artikel ini, kami menghuraikan proses Ornstein-Uhlenbeck, menerangkan formula matematiknya, dan memberikan pelaksanaan asas Python untuk mensimulasikan versi perpecahan SDE yang berterusan. Dalam artikel seterusnya, kami akan mengkaji SDE yang lebih kompleks yang dibina berdasarkan proses OU dan bagaimana mereka digunakan dalam perdagangan sistem dan aplikasi harga derivatif.

Kod lengkap

# OU process simulation

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 30.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

Pautan ke artikel asal: https://www.quantstart.com/articles/ornstein-uhlenbeck-simulation-with-python/