Bolehkah anda mengatasi gorila dengan bertaruh (berdagang) dengan mesin vektor SVM?

Tuan-tuan dan puan-puan, pertaruhkan taruhan anda. Hari ini, kita akan berusaha keras untuk mengalahkan seekor orang utan, yang dianggap sebagai salah satu pesaing paling menakutkan dalam dunia kewangan. Kami akan cuba meramalkan keuntungan hari berikutnya untuk jenis perdagangan mata wang yang berlainan. Saya jamin kepada anda: walaupun untuk mengalahkan orang utan yang bertaruh secara rawak dan mendapat peluang 50% untuk menang, ia adalah satu perkara yang sukar. Kami akan menggunakan algoritma pembelajaran mesin yang sedia ada yang menyokong penjenamaan vektor. Mesin vektor SVM adalah kaedah yang sangat kuat untuk menyelesaikan tugas regresi dan klasifikasi.

• SVM menyokong mesin vektor

Mesin vektor SVM adalah berasaskan idea bahawa kita boleh menggunakan hyperplane untuk membezakan ruang ciri p. Algoritma mesin vektor SVM menggunakan hyperplane dan Margin pengenalan untuk mewujudkan sempadan keputusan klasifikasi, seperti yang ditunjukkan di bawah.

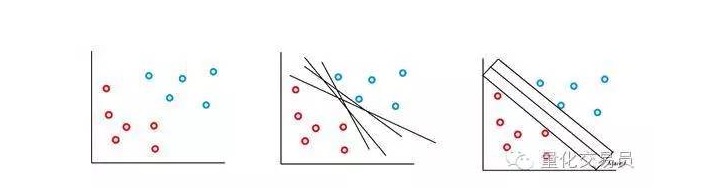
Dalam kes yang paling mudah, klasifikasi linear adalah mungkin. Algoritma memilih sempadan keputusan, yang dapat memaksimumkan jarak antara kelas.

Dalam kebanyakan siri masa kewangan yang anda hadapi, anda tidak mungkin menemui kumpulan yang mudah dan linear yang boleh dipisahkan, tetapi ia sering berlaku. Mesin vektor SVM menyelesaikan masalah ini dengan menerapkan kaedah yang dikenali sebagai kaedah margin lembut.

Dalam kes ini, beberapa kes klasifikasi yang salah dibenarkan, tetapi mereka sendiri menjalankan fungsi untuk meminimumkan faktor dan jarak ke sempadan yang salah untuk menjadikan C (kesalahan kos atau anggaran boleh dibenarkan) berbanding lurus.

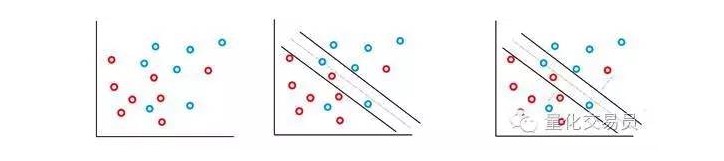
Pada asasnya, mesin akan memaksimumkan jarak antara klasifikasi dan meminimumkan hukuman yang ditanggung oleh C.

Classifier SVM mempunyai satu ciri yang hebat ialah kedudukan dan saiz sempadan keputusan klasifikasi ditentukan hanya oleh sebahagian daripada data, iaitu bahagian yang paling dekat dengan sempadan keputusan. Sifat algoritma ini membolehkan ia untuk menentang gangguan nilai luar biasa jarak jauh.

Adakah ia terlalu rumit? baiklah, saya fikir keseronokan baru bermula.

Pertimbangkan keadaan berikut ((separasikan titik merah dan warna lain):

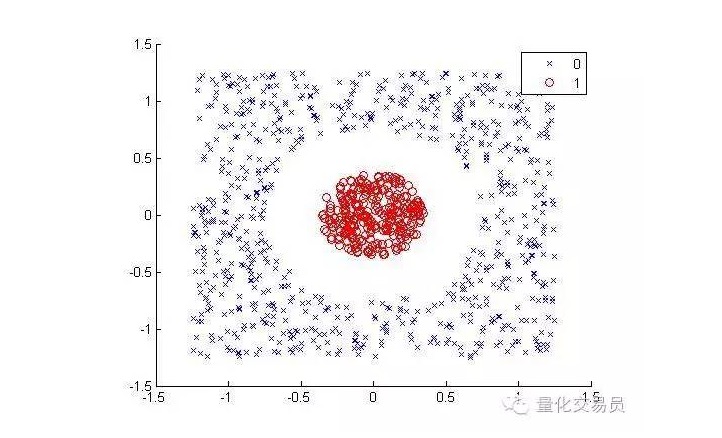
Bagi manusia, ia mudah untuk diklasifikasikan (sesuatu yang boleh dilakukan dengan satu garis bujur) tetapi tidak sama untuk mesin. Jelas sekali, ia tidak boleh dibuat menjadi garis lurus (satu garis lurus tidak dapat memisahkan titik merah). Di sini kita boleh mencuba teknik kernel.

Teknik inti adalah teknik matematik yang sangat bijak yang membolehkan kita menyelesaikan masalah klasifikasi linear dalam ruang dimensi tinggi. Sekarang mari kita lihat bagaimana ia dilakukan.

Kami akan menukar ruang ciri dua dimensi ke tiga dimensi dengan pemetaan peningkatan, dan kembali ke dua dimensi selepas selesai mengklasifikasikan.

Di bawah ini adalah imej pemetaan dan pengelompokan:

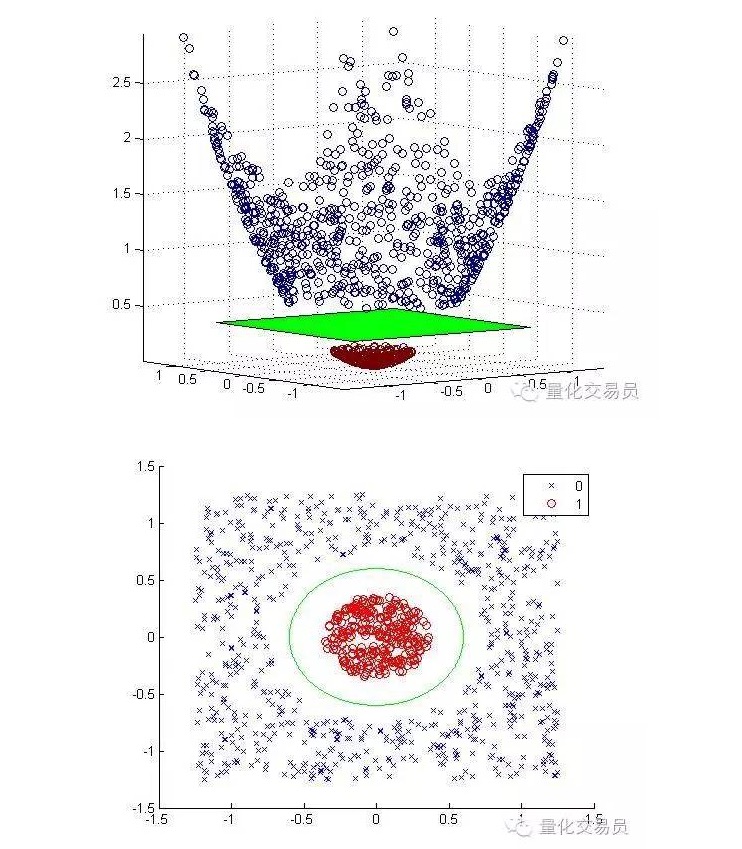
Secara umum, jika terdapat d input, anda boleh memetakan ruang input d dimensi ke ruang ciri p dimensi menggunakan satu pemetaan. Jalankan penyelesaian yang akan dihasilkan oleh algoritma pengurangan di atas, dan kemudian memetakan kembali ruang input asal anda ke p dimensi superplank.

Asas penting penyelesaian matematik di atas adalah bagaimana menghasilkan set sampel titik yang baik dalam ruang ciri.

Anda hanya memerlukan set sampel titik ini untuk melakukan pengoptimuman sempadan, pemetaan tidak perlu jelas, dan titik-titik ruang input dalam ruang ciri berdimensi tinggi boleh dikira dengan selamat melalui fungsi teras ((dan sedikit bantuan teorema Mercer)).

Sebagai contoh, anda ingin menyelesaikan masalah klasifikasi anda dalam ruang ciri yang sangat besar, katakanlah 100,000 dimensi. Bolehkah anda bayangkan kuasa pengiraan yang anda perlukan? Saya sangat meragui sama ada anda dapat menyelesaikannya.

• Cabaran dan Gorila

Sekarang kita bersiap sedia untuk menghadapi cabaran untuk mengalahkan Jeff yang mampu meramalkan apa yang akan berlaku.

Jeff adalah seorang pakar dalam pasaran wang dan dia boleh membuat ramalan dengan keakuratannya sebanyak 50% melalui pertaruhan rawak, yang merupakan isyarat untuk meramalkan kadar keuntungan pada hari dagangan berikutnya.

Kami akan menggunakan pelbagai siri masa asas, termasuk siri masa harga langsung, setiap siri masa dengan keuntungan sehingga 10 lags, dengan jumlah 55 ciri.

Mesin vektor SVM yang akan kita bina adalah dengan menggunakan kernel 3 darjah. Anda boleh bayangkan bahawa memilih kernel yang sesuai adalah satu lagi tugas yang sangat sukar, untuk menyelaraskan parameter C dan Γ, triple cross-validate berjalan pada grid kombinasi parameter yang mungkin, dan kumpulan terbaik akan dipilih.

Hasilnya tidak begitu menggembirakan:

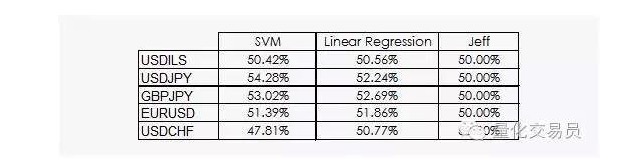
Kita dapat melihat bahawa sama ada regresi linear atau mesin vektor SVM dapat mengalahkan Jeff. Walaupun hasilnya tidak optimis, kita juga dapat memperoleh beberapa maklumat dari data, yang merupakan berita baik, kerana dalam bidang data, siri masa kewangan tidak paling berguna.

Set data akan dilatih dan diuji selepas cross-validation, dan kami merekodkan kebolehan ramalan SVM yang dilatih, dan untuk prestasi yang stabil, kami mengulangi pembahagian rawak setiap mata wang 1000 kali.

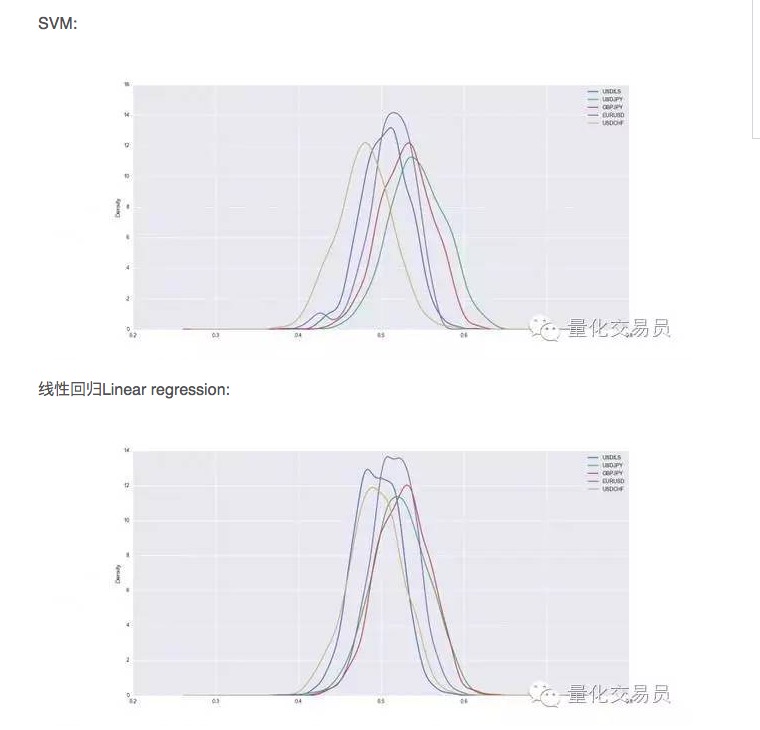
Oleh itu, dalam beberapa kes, SVM lebih baik daripada regresi linear yang mudah, tetapi perbezaan prestasi juga sedikit lebih tinggi. Sebagai contoh, dalam USD / JPY, isyarat yang kita boleh meramalkan rata-rata 54% daripada jumlah keseluruhan. Ini adalah hasil yang cukup baik, tetapi mari kita lihat lebih dekat!

Ted adalah sepupu Jeff, dan tentu saja ia juga seekor gorila, tetapi ia lebih bijak daripada Jeff. Ted menumpukan perhatian kepada set sampel latihan, dan bukannya pertaruhan rawak.

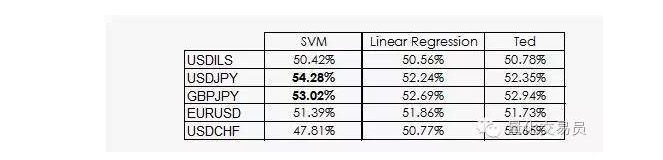
Seperti yang kita lihat, prestasi kebanyakan SVM hanya datang dari satu fakta: pembelajaran mesin bahawa klasifikasi tidak mungkin sama dengan keutamaan. Sebenarnya, regresi linear tidak dapat memperoleh apa-apa maklumat dari ruang ciri, tetapi intercept () dalam regresi masuk akal, dan fakta bahawa intercept berkait rapat dengan klasifikasi lebih baik.

Satu berita yang sedikit lebih baik ialah bahawa mesin vektor SVM dapat mengambil maklumat tambahan dari data yang tidak linear, yang membolehkan kita untuk mencadangkan ketepatan ramalan sebanyak 2%.

Malangnya, kita tidak tahu apa jenis maklumat ini, sama seperti mesin vektor SVM mempunyai kelemahan utama sendiri, yang tidak dapat kita jelaskan.

Penulis: P. López, diterbitkan dalam quantdare Dipetik daripada WeChat Public