Buku pesanan strategi perdagangan frekuensi tinggi berdasarkan pembelajaran mesin

• ### I. Perkataan

Mekanisme perdagangan di pasaran sekuriti boleh dibahagikan kepada dua jenis pasaran yang didorong oleh tawaran dan pasaran yang didorong oleh pesanan, yang pertama bergantung kepada penyediaan kecairan oleh peniaga pasaran, yang kedua adalah penyediaan kecairan melalui borang harga terhad, yang diperdagangkan melalui pembelian dan penjualan yang ditugaskan oleh pelabur. Pasaran sekuriti China adalah pasaran yang didorong oleh pesanan, termasuk pasaran saham dan pasaran niaga hadapan.

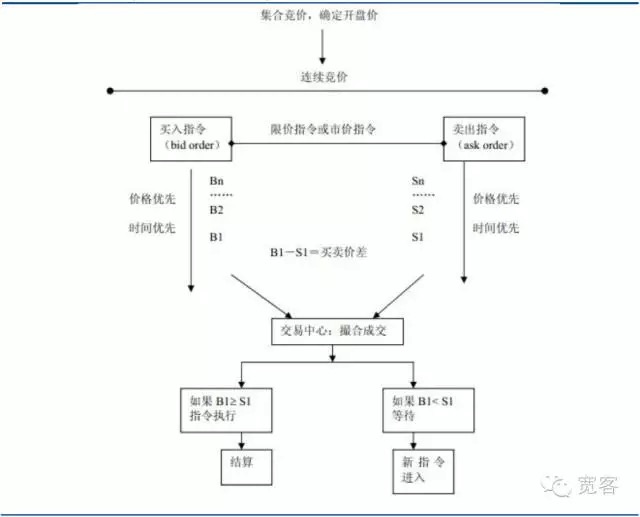Rajah 1 Peta pasaran yang didorong oleh pesanan

• (a) Buku pesanan harga terhad

  Kajian buku pesanan berada dalam bidang penyelidikan struktur mikro pasaran, teori struktur mikro pasaran mengambil teori harga dan teori pembekal dalam ekonomi mikro sebagai sumber pemikirannya, dan dalam analisis proses dan sebab-sebab pembentukan harga dan perdagangan aset kewangan dalam masalah utamanya, ia menggunakan pelbagai teori dan kaedah seperti keseimbangan umum, keseimbangan tempatan, keuntungan marginal, kos marginal, kesinambungan pasaran, teori stok, teori permainan, dan ekonomi maklumat.

  Dari segi kemajuan penyelidikan di luar negara, O’Hara diwakili dalam bidang struktur mikro pasaran, kebanyakan teori adalah berdasarkan pasaran peniaga pasaran (iaitu pasaran yang didorong oleh tawaran), seperti model inventori dan model maklumat. Tahun ini, didorong oleh pesanan telah secara beransur-ansur menduduki bahagian atas dalam pasaran transaksi sebenar, tetapi kajian khusus terhadap pasaran didorong oleh pesanan masih kurang.

  Pasaran sekuriti domestik dan pasaran niaga hadapan adalah pasaran yang didorong oleh pesanan, gambar di bawah adalah skrin buku pesanan Level_1 untuk kontrak niaga hadapan indeks saham IF1312. Tidak banyak maklumat yang diperoleh secara langsung dari atas, maklumat asasnya termasuk harga beli, harga jual, pembelian satu jumlah dan penjualan satu jumlah. Dalam beberapa kertas akademik di luar negara, ada buku pesanan yang sesuai dengan buku pesanan, termasuk data pengumpulan pesanan yang paling terperinci, setiap termasuk pesanan pesanan, harga transaksi, jenis pesanan dan lain-lain.

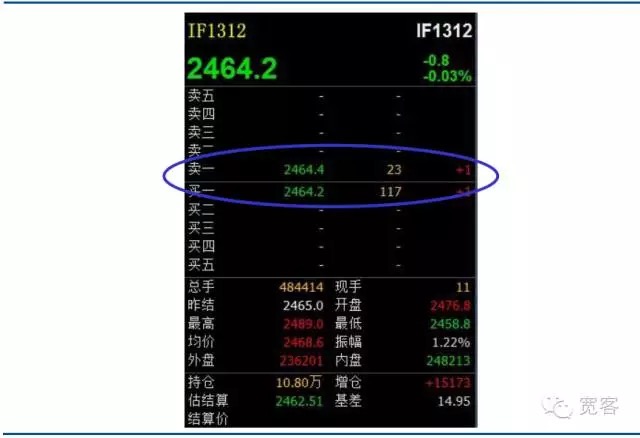  Rajah 2 Indeks Saham FUTURES Kontrak Utama Tahap-1 Buku Pesanan

• (ii) Kemajuan dalam penyelidikan perdagangan frekuensi tinggi buku pesanan

  Model dinamik buku pesanan, terdapat dua kaedah utama, satu adalah kaedah ekonomi metrik klasik, yang lain adalah kaedah pembelajaran mesin. Kaedah ekonomi metrik adalah kaedah penyelidikan arus perdana klasik, seperti pemecahan MRR untuk analisis perbezaan harga, pemecahan Huang dan Stoll, model ACD untuk jangka masa pesanan, model Logistic untuk ramalan harga.

  Pembelajaran mesin dalam bidang kewangan juga sangat aktif dalam penyelidikan akademik, seperti pada tahun 2012 di MalaysiaPredcasting trends of high_frequency KOSPI200 index data using learning classifiersPredcasting trends of high_frequency KOSPI200 index data using learning classifiersPredicting trends of high_frequency KOSPI200 index data using learning classifiersPredicting trends of high_frequency KOSPI200 index data using learning classifiersPredicting trends of high_frequency KOSPI200 index data using learning classifiersPredicting trends of high_frequency KOSPI200 index data using learning classifiersPredicting trends of high_frequency KOSPI200 index data using learning classifiersPredicting trends of high_frequency KOSPI200 index data using learning classifiers

• Aplikasi Pembelajaran Mesin dalam Perdagangan Frekuensi Tinggi Buku Perintah

  • #### (I) Peta struktur sistem

  Gambar di bawah ini adalah kerangka sistem untuk strategi perdagangan pembelajaran mesin yang tipikal, termasuk data buku pesanan, penemuan ciri, pembinaan dan pengesahan model dan beberapa modul utama peluang perdagangan. Perlu diperhatikan bahawa proses perdagangan dicetuskan oleh peristiwa trend, dengan kedatangan tick trend sebagai salah satu peristiwa.

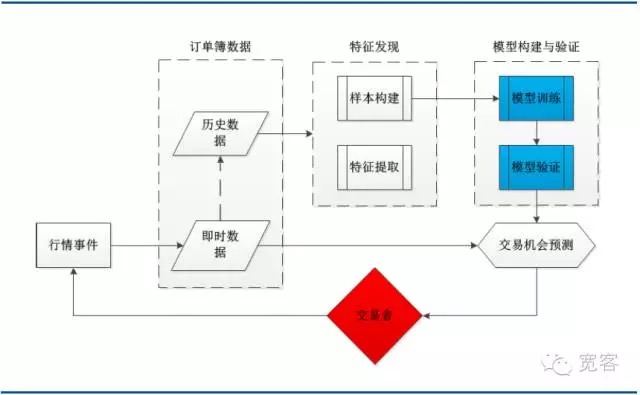  Rajah 3 Arkitektur sistem untuk pemodelan buku pesanan berdasarkan pembelajaran mesin

  • #### (ii) Maklumat Pembantu

  Pada tahun 1970-an, Vapnik dan lain-lain mula membina satu set sistem teori yang lebih lengkap untuk teori pembelajaran statistik (SLT), yang digunakan untuk mengkaji sifat peraturan statistik dan kaedah pembelajaran dalam keadaan sampel terhad, mewujudkan kerangka teori yang baik untuk masalah pembelajaran mesin sampel terhad, menyelesaikan masalah praktikal seperti sampel kecil, bukan linear, dimensi tinggi dan titik terendah tempatan. Pada tahun 1995, Vapnik dan lain-lain secara jelas mengemukakan satu kaedah pembelajaran universal baru untuk menyokong vektor mesin (SVM, Support Vector Machine), teori ini mendapat perhatian yang luas dan digunakan dalam pelbagai bidang, yang pada mulanya menunjukkan prestasi yang lebih baik daripada kaedahnya sendiri.

  SVM adalah perkembangan daripada supra-permukaan klasifikasi yang optimum dalam kes pembahagian linear. Untuk soalan klasifikasi dua kelas, letakkan kumpulan sampel latihan sebagai ((xi,yi), i = 1,2…l, l adalah bilangan sampel latihan, xi adalah sampel latihan, yi adalah milik {-1 + 1} sebagai penanda kelas input sampel xi ((output yang diharapkan). Titik permulaan algoritma SVM adalah mencari supra-permukaan klasifikasi yang optimum.

  Klasifikasi superplan yang optimum bukan sahaja dapat memisahkan semua sampel dengan betul, tetapi juga dapat menjadikan margin antara kedua-dua kategori sebagai maksimum. Margin ini ditakrifkan sebagai jumlah jarak minimum dari kumpulan data latihan ke superplan klasifikasi tersebut. Klasifikasi superplan yang optimum bermaksud bahawa rata-rata kesalahan klasifikasi terhadap data ujian adalah minimum.

  Jika terdapat satu superplan dalam ruang vektor dimensi d:

  F(x)=w*x+b=0

  Untuk memisahkan kedua-dua jenis data di atas, kita boleh menyebutnya sebagai antara muka.*x ialah dua vektor w dan x dalam ruang vektor dimensi d.

  Jika muka depan:

  w*x+b=0

  Margin yang membolehkan jarak antara dua jenis sampel yang paling dekat antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara antara

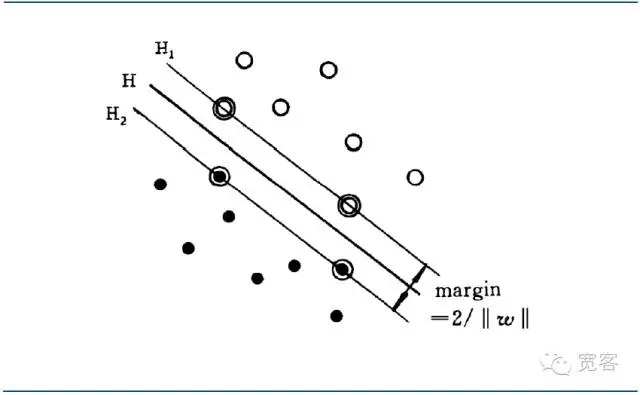  Rajah 4 Grafik antara muka optimum bagi SVM

  Dengan penyesuaian persamaan antara dua jenis sampel, jarak antara kedua-dua jenis sampel dapat disatukan.

  

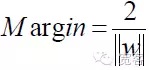
  Jadi untuk setiap sampel, terdapat

  

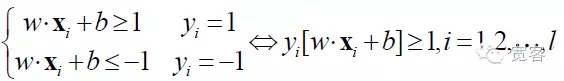
  Untuk mendapatkan antara muka yang optimum, selain memenuhi formula di atas, anda juga perlu meminimumkannya.

  Oleh itu, model matematik untuk masalah SVM adalah:

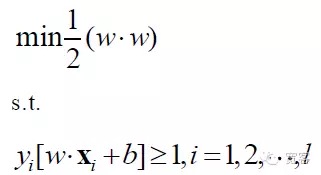
  SVM akhirnya menjadi masalah perancangan yang paling optimum, dan fokus penyelidikan akademiknya adalah untuk penyelesaian cepat, penyebaran ke pelbagai kelas, aplikasi masalah praktikal, dan sebagainya.

  SVM pada mulanya ditujukan untuk masalah klasifikasi dua, dan mengikut keperluan aplikasi sebenar, ia dilancarkan ke masalah pelbagai kelas. Algoritma pelbagai kelas yang sedia ada termasuk satu pasang, satu pasang, kod pembetulan ralat, DAG-SVM dan pengklasifikasi SVM i-kelas, dll.

  • #### (iii) Pengekstrakan Indeks Buku Pesanan

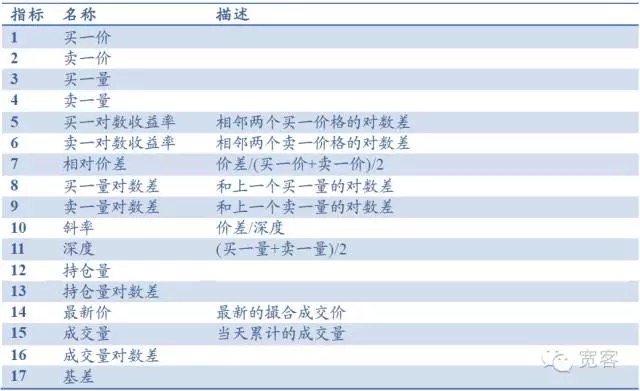
  Sebagai contoh, buku pesanan terdiri daripada indikator asas seperti harga beli satu, harga jual satu, kuantiti beli satu, kuantiti jual satu, dan boleh menghasilkan indikator seperti kedalaman, kecenderungan, perbezaan harga relatif, indikator lain termasuk jumlah pegangan, jumlah transaksi, perbezaan asas, dan lain-lain, sebanyak 17 indikator, seperti yang ditunjukkan dalam jadual di bawah. Indikator analisis teknikal yang biasa seperti RSI, KDJMA, EMA, dan lain-lain juga boleh diperkenalkan.

  Jadual 1 Perpustakaan petunjuk berdasarkan buku pesanan Level

  

  • #### (iv) Penulisan ciri-ciri dinamik dan peluang dagangan dalam buku pesanan

  Dari sudut mikro pasaran, terdapat dua cara untuk mengukur pergerakan harga dalam masa yang singkat, satu adalah pergerakan harga pertengahan, dan yang lain adalah perbezaan harga silang. Dalam artikel ini, kami memilih pergerakan harga pertengahan yang lebih mudah dan intuitif.

  

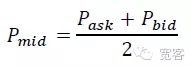
  Berdasarkan buku pesanan dalam Δt saiz perubahan harga pertengahan ΔP dibahagikan kepada tiga kategori kenaikan dan penurunan.

  Graf di bawah adalah peredaran pergerakan harga pertengahan kontrak IF1311 pada 29 Oktober, dengan 32400 tick setiap hari.

  Dalam keadaan Δt = 1tick, nilai mutlak perubahan harga pertengahan adalah kira-kira 0.2 kali, nilai mutlak perubahan adalah kira-kira 0.4 kali, nilai mutlak perubahan adalah kira-kira 150 kali, nilai mutlak perubahan adalah lebih besar daripada 0.8 kali, dan nilai mutlak perubahan lebih besar daripada sama dengan 1 kira-kira 10 kali.

  Dalam keadaan Δt = 2tick, nilai mutlak perubahan harga pertengahan adalah 0.2 kira-kira 7000 kali, nilai mutlak perubahan 0.4 kira-kira 3000 kali, nilai mutlak perubahan 0.6 kira-kira 550 kali, nilai mutlak perubahan 0.8 kira-kira 205 kali, dan nilai mutlak perubahan lebih besar daripada sama dengan 1 kira-kira 10 kali.

  Kami menganggap peluang yang berpotensi apabila nilai mutlak perubahan lebih besar daripada atau sama dengan 0.4. Dalam kes Δt = 1 tick, terdapat kira-kira 1700 peluang setiap hari; Dalam kes Δt = 2 tick, terdapat kira-kira 4000 peluang setiap hari.

  

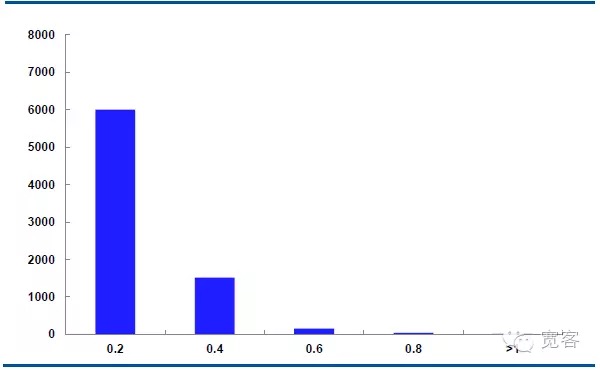
  Rajah 5 IF1311 Perkembangan harga pertengahan pada 29 Oktober (Δt = 1 tick)

  

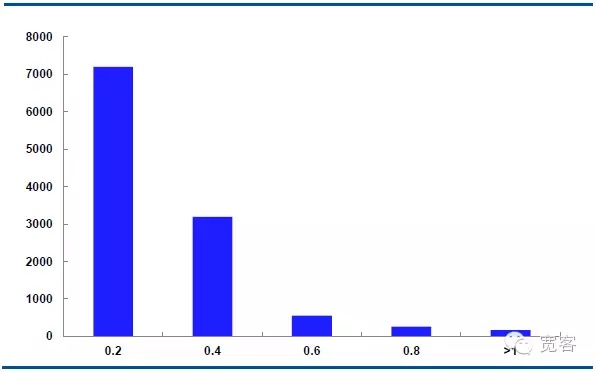
  Rajah 6 IF1311 Perkembangan harga pertengahan pada 29 Oktober (Δt=2tick)

• Ketiga, bukti strategi

Oleh kerana model SVM mempunyai kerumitan latihan yang lebih tinggi dalam keadaan sampel besar dan masa latihan yang lebih lama, kami memilih data keadaan sejarah dengan jangka masa yang lebih pendek, dengan contoh data keadaan Level_1 kontrak IF1311 pada bulan Oktober, untuk mengesahkan kesahihan model.

• (I) Ujian Kesan Model

  Tempoh data: data mengenai kontrak IF1311 pada bulan Oktober;

  Pengharaman Δt: Semakin kecil Δt, semakin tinggi keperluan untuk perincian urus niaga, apabila Δt = 1 tick, sukar untuk mendapatkan keuntungan dalam urus niaga sebenar, untuk membandingkan kesan model, nilai 1 tick, 2 tick, 3 tick;

  Penunjuk penilaian model: ketepatan sampel, ketepatan ujian, masa ramalan. 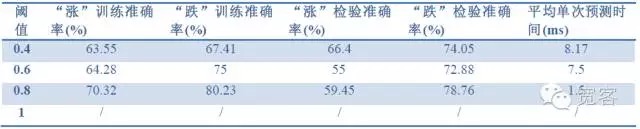Jadual 2 Menganggarkan kesan 1 tick dengan data 1 tick

  Jadual 3 Menganggarkan kesan tick2 dengan data tick1

  Jadual 4 Menganggarkan kesan 2tick dengan data 2tick

  Dari tiga jadual di atas, kita boleh membuat beberapa kesimpulan: Ketepatan maksimum adalah kira-kira 70%, dan apabila ketepatan mencapai 60%, ia boleh diterjemahkan ke dalam strategi perdagangan.

• (ii) Hasil simulasi strategi

  Sebagai contoh, pada 31 Oktober, kami melakukan perdagangan simulasi, bayaran pemprosesan dagangan indeks saham institusi adalah 0.²⁶⁄₁₀₀₀₀, kami mengandaikan jumlah dagangan tanpa had penerimaan, dengan harga satu sisi 0.2 mata setiap dagangan, dan satu tangan setiap pesanan.

  Jadual 5 Simulasi Strategi pada 31 Oktober

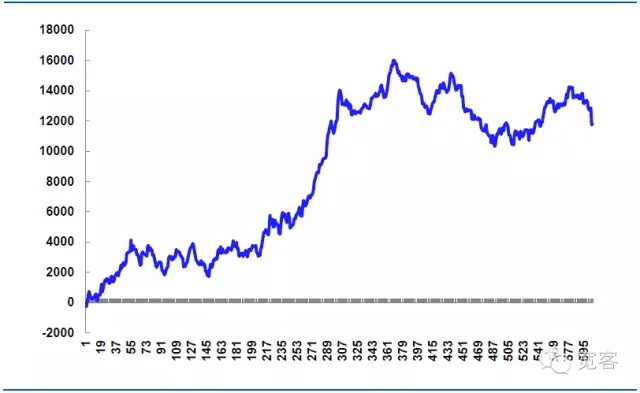
  605 kali dagangan sepanjang hari, 339 kali keuntungan, 56% kemenangan, keuntungan bersih 11814.99 yuan.

  Theoretical harga peluru adalah 14,520 yuan, ini adalah sebahagian daripada kunci strategi pertempuran, jika butiran pesanan yang lebih halus dikawal, maka boleh mengurangkan harga peluru, meningkatkan keuntungan bersih, jika butiran pesanan yang tidak betul dikawal, atau pasaran turun naik yang tidak normal, harga peluru akan lebih besar, dan keuntungan bersih akan berkurang, oleh itu kejayaan perdagangan frekuensi tinggi sering bergantung kepada pelaksanaan butiran.

  Rajah 7 Keuntungan strategi simulasi pada 31 Oktober

Pengumuman asal: Artikel ini ditulis oleh penulis asal, dan boleh dirakamkan dengan menyatakan sumbernya.