Formula Kelly - alat yang berkuasa untuk mengawal kedudukan

** Anggap lotere 1: anda menang 60% dan anda kalah 40%; anda menang 100% dan anda kalah 100%. Jika anda menang, anda akan menang \( 1 untuk setiap \) 1, dan jika anda kalah, anda akan kehilangan \( 1 untuk setiap \) 1. Anda boleh bermain lotere tanpa had dan anda boleh membuat taruhan anda sendiri.

• 1. Untuk permainan ini, setiap pertaruhan anda akan mendapat 60 peratus daripada jumlah yang anda pertaruhkan.*1-40%*1 = 20%, dan jangkaan keuntungan adalah positif. Iaitu, ia adalah satu kebuntuan di mana penjenayah mempunyai kelebihan, dan mempunyai kelebihan yang besar.

Jadi, bagaimana kita boleh bertaruh?

Jika kita tidak berfikir dengan teliti, bayangkan secara kasar, kita akan berfikir bahawa kerana keuntungan yang saya harapkan setiap kali saya berjudi adalah 20%, maka untuk mencapai keuntungan maksimum dalam jangka panjang, saya harus berusaha untuk meletakkan lebih banyak peratusan modal dalam setiap pertaruhan.

Tetapi jelas setiap pertaruhan pertaruhan meletakkan 100% dari modal adalah tidak munasabah, kerana jika mana-mana pertaruhan pertaruhan kalah, maka semua modal akan hilang, tidak dapat lagi mengambil bahagian dalam pertaruhan berikutnya, hanya boleh pergi dengan tenang.

Oleh itu, kesimpulannya adalah bahawa jika terdapat peluang untuk kehilangan semua dana anda dalam satu-satu masa, walaupun kemungkinan itu sangat kecil, maka anda tidak akan pernah dapat memenuhi kedudukan anda. Kerana dalam jangka masa panjang, peristiwa kecil kemungkinan mesti berlaku, dan dalam kehidupan sebenar, kemungkinan sebenar peristiwa kecil kemungkinan berlaku jauh lebih besar daripada kebarangkalian teorinya. Itulah kesan ekor lemak dalam bidang kewangan.

• 2 . Kembali ke titik 1. Jika setiap kali anda bertaruh 100% adalah tidak masuk akal, bagaimana dengan 99%? Jika anda bertaruh 99% setiap kali, anda tidak hanya dijamin tidak akan pernah bangkrut, tetapi jika anda bernasib baik, anda mungkin akan mendapat keuntungan yang besar.

Adakah ini yang sebenarnya berlaku?

Kita tidak perlu mengkaji masalah ini secara teori, kita boleh membuat eksperimen. Kita mensimulasikan keadaan yang tidak menentu ini, dan setiap kali kita bertaruh 99%, kita akan melihat hasilnya.

Eksperimen simulasi ini sangat mudah dan boleh dilakukan dengan menggunakan Excel. Lihat rajah berikut:

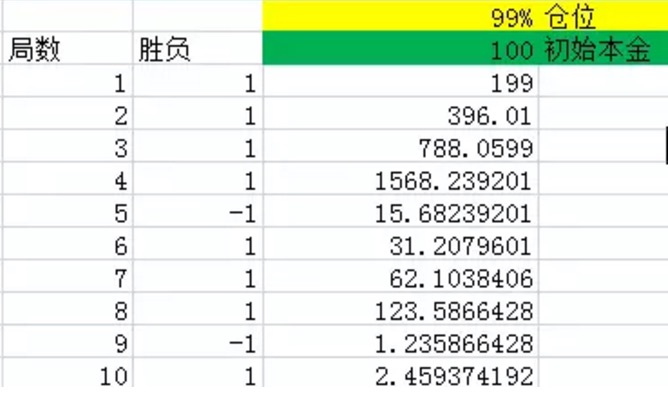Rajah 1

Seperti yang ditunjukkan di atas, lajur pertama menunjukkan jumlah permainan. Lajur kedua adalah kemenangan, Excel akan menghasilkan 1 mengikut kebarangkalian 60%, iaitu kebarangkalian 60% untuk keuntungan bersih 1,40% untuk keuntungan bersih -1, iaitu kebarangkalian 40% untuk keuntungan bersih -1. Lajur ketiga adalah semua dana yang dikhaskan pada akhir setiap permainan.

Anda dapat melihat dari gambar, selepas 10 putaran, peluang untuk menang dalam 10 putaran adalah 8, lebih besar daripada 60%, hanya kalah dua kali. Tetapi walaupun begitu, wang terakhir hanya tinggal 2.46 yuan, pada dasarnya adalah kehilangan cahaya.

Dan apabila saya meningkatkannya kepada 1,000, 2,000, 3,000, anda boleh bayangkan, pada akhirnya, jumlah wang yang ada pada tangan saya adalah hampir sama dengan 0.

Oleh kerana 99% tidak berfungsi, mari kita cuba dengan beberapa perkadaran lain, seperti yang ditunjukkan di bawah: Dari gambar ini dapat dilihat bahawa apabila kedudukan dikurangkan dari 99%, menjadi 90%, 80%, 70%, 60%, hasil 10 putaran yang sama akan menjadi sama sekali berbeza. Dari gambar ini dapat dilihat bahawa dengan kedudukan yang semakin kecil, dana setelah 10 putaran semakin besar.

Jika anda melihat di sini, anda akan sedar bahawa masalah ini tidak semudah itu. Walaupun ia adalah satu pertaruhan yang sangat besar yang dikendalikan oleh penjenayah, ia tidak boleh dimenangi dengan mudah.

Jadi, bagaimana anda boleh bertaruh untuk mendapatkan keuntungan maksimum dalam jangka masa panjang?

Tidak semestinya, kerana anda tidak akan dapat menjana wang apabila nisbah anda menjadi sifar.

Jadi, berapa nisbah optimum?

Ini adalah masalah yang perlu diselesaikan dengan formula Kelly yang terkenal!

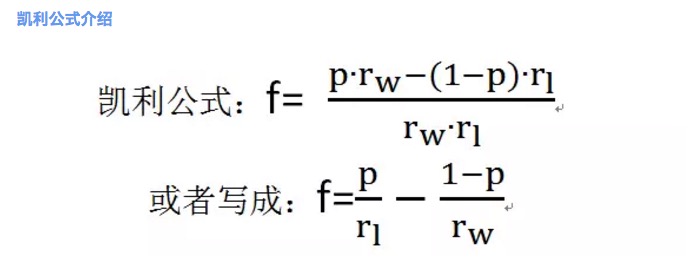Rajah 2

Di mana f adalah peratusan pertaruhan yang optimum. p adalah kebarangkalian untuk menang. rw adalah kadar keuntungan bersih apabila menang, contohnya dalam permainan 1 rw = 1. rl adalah kadar kerugian bersih apabila kalah, contohnya dalam permainan 1 rl = 1. Perhatikan di sini rl> 0 .

Berdasarkan formula Kelly, peratusan pertaruhan maksimum dalam pertaruhan 1 boleh dikira sebagai 20%.

Kita boleh melakukan eksperimen untuk memahami kesimpulan ini.

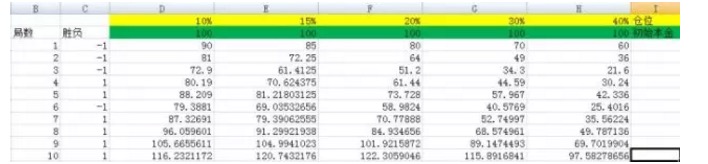Rajah 3

Seperti yang ditunjukkan, kita menetapkan kedudukan masing-masing sebagai 10%, 15%, 20%, 30%, 40% ❚ Mereka masing-masing mempunyai D, E, F, G, H ❚.

Dan apabila saya mengubahnya kepada 3,000, saya mendapat lebih banyak lagi. Dan saya akan cuba untuk membetulkannya, dan saya akan cuba untuk mengubahnya. Dari sini anda dapat melihat bahawa hasil yang sesuai dengan lajur F adalah yang terbesar, dan akar tekanan berbanding dengan lajur lain bukanlah satu kuantitatif.

Anda lihat kuasa formula Kelly. Dalam eksperimen di atas, jika anda tidak bernasib baik untuk memilih nisbah 40%, iaitu set H, maka selepas 5000 pertaruhan, walaupun modal anda dari 100 menjadi 22799985.75, keuntungan yang besar. Tetapi berbanding dengan hasil nisbah 20%, itu sama dengan tidak menghasilkan wang.

Inilah kuasa pengetahuan!

• 3. Memahami persamaan Kelly

Kesimpulan matematik formula Kelly dan kerumitan, memerlukan pengetahuan matematik yang sangat tinggi dan mendalam, jadi tidak ada gunanya untuk membincangkannya di sini. Di sini saya akan memperdalam pemahaman subjektif anda tentang formula Kelly melalui beberapa eksperimen.

Mari kita lihat satu lagi pertaruhan. Pertaruhan 2: peluang anda untuk kalah dan menang adalah 50%, contohnya dengan membuang syiling. Apabila anda menang, kadar keuntungan bersih adalah 1, iaitu rw = 1, dan apabila anda kalah, kadar kerugian bersih adalah 0.5, iaitu rl = 0.5.

Mudah untuk melihat bahawa keuntungan yang dijangkakan untuk kemerosotan 2 adalah 0.25, satu lagi kemerosotan di mana penjenayah mempunyai kelebihan yang besar.

Berdasarkan formula Kelly, kita boleh mendapatkan peratusan pertaruhan yang optimum untuk setiap permainan ialah:

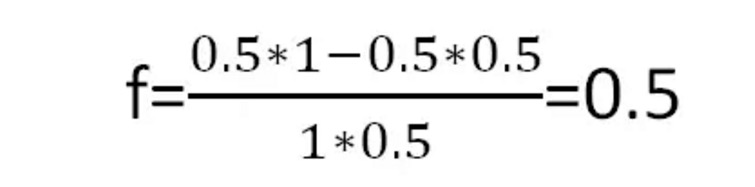Rajah 4

Ini bermakna setiap kali anda bertaruh separuh daripada wang anda, anda akan mendapat keuntungan yang paling besar dalam jangka masa panjang.

Di bawah ini saya akan membuat percubaan untuk mendapatkan konsep kadar pertumbuhan rata-rata r.

Pertama, lihat eksperimen 2.1, dua gambar berikut:

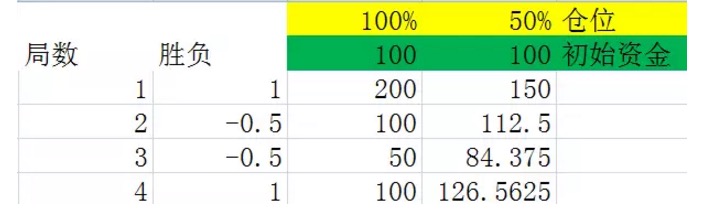Rajah 5

Kedua-dua grafik ini adalah eksperimen yang dilakukan untuk mensimulasikan kemerosotan 2, di dalam lajur kedua, kemerosotan kemenangan menghasilkan kemungkinan 50% 1, yang bermaksud keuntungan 100% ⋅ Kemungkinan 50% menghasilkan -0.5, yang bermaksud kerugian 50%. Kolom ketiga dan keempat adalah dana yang dimiliki selepas setiap kemerosotan di bawah kedudukan 100% dan 50% masing-masing ⋅

Dengan teliti membandingkan kedua-dua carta dapat menemui kesimpulan pertama, iaitu selepas melalui jumlah yang sama, hasil akhir hanya berkaitan dengan jumlah yang menang dan jumlah yang kalah dalam jumlah ini, dan tidak berkaitan dengan urutan yang menang dan kalah dalam jumlah ini. Sebagai contoh, dalam kedua-dua gambar sebelumnya, 4 permainan juga dilakukan, juga dua kemenangan dan dua kekalahan dalam setiap gambar, tetapi urutan yang kalah dalam gambar pertama adalah menang dan kalah, urutan yang kalah dalam gambar kedua adalah kalah dan menang.

Sudah tentu kesimpulan ini sangat mudah untuk dibuktikan (hukum pertukaran perkalian, kanak-kanak sekolah rendah akan tahu), tetapi ia tidak dibuktikan di sini, dua contoh di atas cukup untuk difahami oleh semua orang.

Oleh itu, kerana keputusan akhir tidak bergantung kepada kemenangan atau kekalahan, mari kita anggap kesunyian 2 berlaku seperti dalam eksperimen 2.2, seperti yang ditunjukkan dalam rajah berikut:

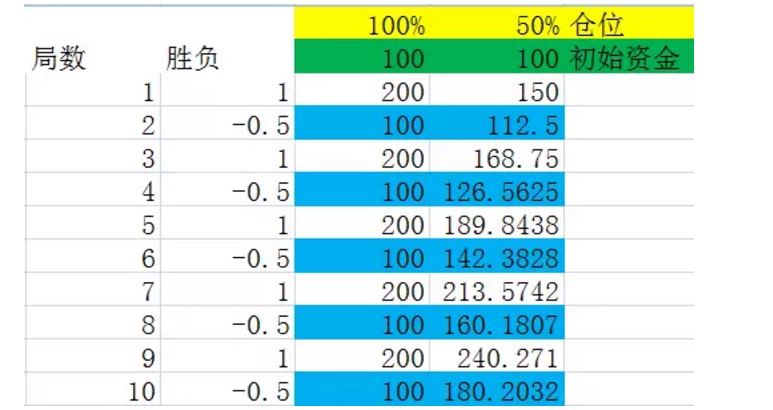Rajah 6

Kami mengandaikan bahawa kemenangan dan kekalahan dalam loteri adalah bergilir-gilir, kerana kesimpulan pertama, dalam jangka masa panjang, tidak ada kesan terhadap hasil.

Sebelum kita melihat gambar itu sendiri, mari kita buat definisi. Jika kita menganggap beberapa set permainan sebagai satu kesatuan, di mana frekuensi pelbagai hasil adalah sama dengan kebarangkalian, dan jumlah permainan dalam kesatuan ini adalah yang terkecil dari semua kesatuan yang memenuhi syarat, maka kita akan menyebut kesatuan ini sebagai satu set permainan.

Perhatikan dengan teliti nombor-nombor yang ditandakan biru dalam carta di atas, mereka adalah akhir sekumpulan kemelut. Anda akan mendapati bahawa angka-angka ini terus meningkat secara stabil. Apabila kedudukan adalah 100%, pertumbuhan nombor yang ditandakan biru adalah 0%, iaitu pertumbuhan modal selepas sekumpulan kemelut adalah 0%. Ini juga menjelaskan bahawa apabila setiap kali kedudukan penuh, ia tidak dapat menghasilkan wang dalam jangka panjang dalam kemelut 2.

Ini adalah undang-undang umum, kadar pertumbuhan selepas setiap kumpulan yang terhenti berkaitan dengan kedudukan. Dan semakin besar kadar pertumbuhan selepas setiap kumpulan yang terhenti, semakin banyak keuntungan akhirnya dalam jangka panjang.

Dalam rajah di atas, jika setiap kumpulan terdiri daripada dua kemelut, maka kadar pertumbuhan rata-rata setiap kemelut

Rajah 7

Dalam jangka masa panjang, untuk mendapatkan pertumbuhan modal yang paling besar, anda perlu memaksimumkan r, iaitu memaksimumkan g. Peratusan pertaruhan terbaik f sebenarnya juga dihasilkan dengan mencari penyelesaian max (g).

• 4. Kesimpulan lain dari persamaan Kelly mengenai risiko

Legenda Kelly

Rumus Kelly pada mulanya ditubuhkan untuk John Larry Kelly, seorang ahli fizik di AT&T Bell Laboratories, berdasarkan kajian rakan sejawatnya, Claude Elwood Shannon, mengenai isyarat dalam talian telefon jarak jauh. Kelly menyelesaikan masalah bagaimana teori maklumat Shannon boleh digunakan untuk seorang penjudi yang mempunyai isyarat dalam talian ketika bermain judi. Penjudi ingin menentukan jumlah pertaruhan terbaik, dan isyarat dalam taliannya tidak perlu sempurna (tidak ada isyarat), yang membolehkan dia mempunyai kelebihan yang berguna. Thorpe menggunakan masa lapang kerjanya, melalui beberapa bulan pengiraan yang sukar, untuk menulis sebuah makalah matematik berjudul “Mengambil 21 mata untuk memilih strategi poker”. Dia menggunakan pengetahuannya sendiri, dan dalam satu malam, dia menyerang semua kasino di Reno, Nevada, dan berjaya memenangi puluhan ribu dolar dari meja 21 mata. Dia juga merupakan nenek moyang dana perlindungan perdagangan kuantitatif di Wall Street, Amerika Syarikat, yang mencipta dana perlindungan perdagangan kuantitatif pertama pada tahun 1970-an.

Menggunakan Perspektif

Bagaimana anda boleh menggunakan formula Kelly untuk menjana wang dalam kehidupan sebenar? Ia adalah untuk mewujudkan kebuntuan yang memenuhi syarat-syarat formula Kelly. Bagi saya, kebuntuan ini mestilah dari pasaran kewangan. Saya baru-baru ini melakukan kajian mengenai sistem perdagangan, apa yang paling penting untuk sistem perdagangan yang baik? Peraturan membeli-belah dengan jangkaan keuntungan positif adalah 10 peratus penting, dan kaedah pengendalian wang yang baik adalah 40 peratus penting, dan selebihnya adalah 50 peratus untuk mengawal mental orang. Dan formula Kelly adalah alat yang membantu saya mengawal kedudukan wang saya. Sebagai contoh, sistem perdagangan saham yang saya kaji sebelum ini, sistem ini melakukan perdagangan seminggu sekali, peluang kejayaan perdagangan setiap minggu adalah 0.8, peluang kegagalan adalah 0.2. Apabila berjaya, anda boleh memperoleh 3% ((mengurangkan komisen, cukai cukai), dan setiap kegagalan rugi 5%. Sebelum mengetahui formula Kelly, saya adalah perdagangan penuh buta, dan tidak tahu kedudukan saya yang ditetapkan tidak betul, mental sangat tidak benar. Selepas menggunakan formula Kelly, kedudukan terbaik yang dikira adalah 9.33. Sudah tentu formula Kelly tidak boleh semudah itu dalam aplikasi praktikal, dan masih banyak kesulitan yang perlu diatasi. Contohnya, kos modal yang diperlukan oleh bursa leasing, misalnya, wang tidak dapat dibahagikan secara tidak terhad dalam realiti, misalnya, tidak semudah itu di pasaran kewangan seperti kemerosotan sederhana yang disebutkan di atas. Tetapi bagaimanapun juga, formula Kelly menunjukkan kepada kita jalan untuk maju.