Matematik dan perjudian

• Kita tahu bahawa perjudian adalah permainan peluang, dan ia adalah beberapa hasil perjudian yang menarik minat ahli matematik Pascal dan ahli matematik besar Fermat, yang melalui surat pertukaran, mengemukakan beberapa prinsip teori kebarangkalian, sehingga menubuhkan teori kebarangkalian. Hari ini saya akan memperkenalkan beberapa topik kebarangkalian dalam perjudian, supaya anda tahu, untuk bertaruh, anda juga perlu memikirkan dengan teliti.

• 1. Perjudian yang sempurna

Ada satu perlawanan antara pasukan NBA, Lakers dan Bulls, dan kedua-dua pasukan mempunyai peminat setia, sebutlah mereka Phoenix dan Bulls. Sudah tentu, peminat merasakan bahawa pasukan yang mereka sokong lebih mungkin untuk menang, jadi mereka akan bertaruh dengan anda. Anggaplah bahawa Phoenix menganggap peluang Lakers untuk menang adalah p, dan Bulls berpendapat bahawa peluang Bulls untuk menang adalah q, p dan q.

Cara ini ialah: kita berjudi dengan wang yang sama seperti wang yang dipertaruhkan oleh orang orang Melayu dan orang Melayu, jika kita menang kita akan mendapat y, jika kita kalah kita akan kehilangan x, dan jika y>x kita akan menang. Dengan x dan y hanya perlu memenuhi dua persamaan mudah berikut, wang yang diharapkan untuk orang Melayu dan orang Melayu akan mendapat keuntungan yang positif, dan akan berjudi dengan kita:

```
p * x - ( 1-p ) * y > 0
q * x - ( 1-q ) * y > 0
```

Ditambah dengan batasan y>x, gambar yang digambarkan adalah kawasan yang dikelilingi oleh tiga garis lurus, untuk nilai koordinat mana-mana titik di dalamnya ((x, y) adalah penyelesaian yang pasti. Jika p>q, penyelesaian adalah bahagian biru dalam gambar berikut:

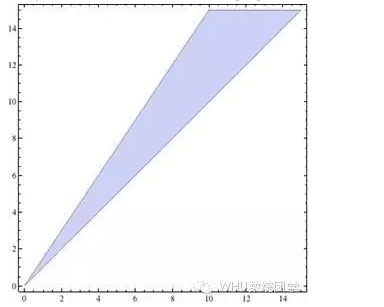
Isu ini seolah-olah telah diselesaikan dengan sempurna, tetapi terdapat satu lagi keraguan, dan saya yakin pembaca akan segera melihat kepalsuannya: sama ada orang Melayu atau orang Melayu, mereka mempunyai jangkaan pendapatan yang positif, iaitu, mereka akan mendapat wang dalam jangka masa panjang, dan kita tidak mendapat apa-apa, jadi dari mana wang yang banyak datang, dan bagaimana mungkin setiap orang mendapat wang?

• ### Penipuan 2 dan 3 Kad

Ini adalah satu lagi teka-teki yang cerdik, kita mulakan dengan tiga kad, kad 1 berhadapan dengan hitam, kad 2 berhadapan dengan merah, kad 3 berhadapan dengan hitam, dan kad 3 berhadapan dengan merah. Kemudian masukkan kad ke dalam kotak, goyangkan, dan biarkan lawan menarik satu kad rata di atas meja.

Sebenarnya peluang kita untuk menang bukanlah ¹⁄₂, tetapi ²⁄₃, dan yang paling mengelirukan dalam permainan ini adalah dua sisi yang terhad pada kad. Pemain tidak mendapat tiga muka, tetapi enam muka: tiga muka hitam, tiga muka merah.

Apabila pemain menarik ke bahagian hitam, iaitu tiga kemungkinan A, C, D, dan seterusnya, bahagian belakang mereka adalah D, F, dan A, dengan hitam menyumbang ²⁄₃ daripada keadaan tersebut.

Masalah ini pertama kali dikemukakan pada tahun 1889 oleh ahli matematik Perancis Joseph Louis François Bertrand, dan kerana hasilnya tidak dijangka, ia juga dikenali sebagai paradoks kotak Bertrand. Pada tahun 1950, ahli matematik Amerika Warren Weaver memperkenalkan permainan kad di atas, yang dipanggil Martin Gardner sebagai penipuan tiga kad.

• ### 3 A. Ceri yang sangat luar biasa

Kadang-kadang kita berjudi akan melepaskan air pada mulanya, biarkan orang lain menang sedikit wang, letakkan tali panjang untuk menangkap ikan besar, dan akhirnya satu-satunya permainan berakhir. Berikut adalah contoh yang sangat baik. Empat orang bermain bridge, saya mula berkata: mari bermain dadu, saya kini mempunyai A, anda meneka saya ada lebih banyak A? Dalam kes ini, anda mungkin akan kalah, dan anda secara diam-diam menetapkan A berwarna, seperti A buah ceri, dan apabila satu putaran menangkap A buah ceri, maka peluang itu datang: bermain dadu lagi, saya kini mempunyai buah ceri A, anda meneka saya tidak mempunyai lebih banyak A?

Ramai orang pasti akan berfikir bahawa dua ketam tidak berbeza sama sekali, ditambah satu buah perisa tidak penting. Tetapi perbezaan di antara mereka sangat luar biasa. Mari kita kira kemungkinan ketam pertama:

  没有A的情形：C（48，13）
  至少有1张A的情形：C（52，13）－C（48，13）
  恰好有1张A的情形：4＊C（48，12）
  至少有2张A的情形：C（52，13）－C（48，13）－4＊C（48，12）
  事件X为至少有两张A，事件Y为至少有一张A，那么条件概率为：

  P（X｜Y）＝P（XY）／P（Y）=(C（52，13）－C（48，13）－4＊C（48，12）)/(C（52，13）－C（48，13）)≈37%

Pada masa ini, saya akan bertaruh bahawa saya mempunyai A, lebih mudah untuk kalah. Tetapi setelah saya memasang taruhan pertama, semua orang berhasrat untuk bertaruh, dan apabila saya melihat bahawa saya tidak mempunyai A lagi, kemungkinan untuk menang adalah jauh berbeza:

  有黑桃A的情形：C（51，12）
  没有其它A的情形：C（48，12）
  还有其它A的情形：C（51，12）－C（48，12）
  事件X为还有其它A，事件Y为有黑桃A，条件概率为：

  P（X｜Y）＝P（XY）／P（Y）＝（C（51，12）－C（48，12））／C（51，12）≈56%。

Dipetik daripada WHU Aritmatika