Mengejar Gadis dan Mencari Peluru Berpandu - Statistik Formula Bayesian

• ### ONE

Orang-orang yang tidak dapat memahami gaya hidup yang tidak masuk akal pasti akan mengalami kejadian sedih seperti ini dalam kehidupan emosional: kebetulan bertemu dengan seorang gadis cantik yang sesuai dengan hati, sejak itu berfikir, tidur dan lupa makan, memulakan perjalanan cinta yang panjang, menunggu hingga satu hari, dalam perselisihan yang tidak berkesudahan, akhirnya mengumpulkan keberanian untuk mengaku kepada gadis itu, akhirnya gadis itu mengatakan bahawa saya sudah mempunyai teman lelaki yang baik dan baik, sangat sukar untuk diterima …

Untuk mengelakkan keadaan yang memalukan ini, bagaimana untuk menentukan sama ada seorang gadis masih bujang atau tidak adalah satu kursus wajib.

Jika anda bekerja dengan seorang gadis, sering berada di sisinya, mengetahui sama ada dia bujang atau tidak bukanlah masalah yang sukar. Tetapi tugas yang sukar yang harus diselesaikan oleh orang yang rasional adalah: sebagai orang asing yang menjaga jarak dengan gadis itu, tanpa disedari oleh gadis itu, anda boleh menilai keadaan bujang gadis itu dengan maklumat yang terhad.

Langkah pertama, percayalah pada naluri anda. Orang yang rasional boleh mempertimbangkan untuk mencari beberapa rakan bersama-sama diam-diam untuk memerhatikan gadis sasaran, tentu saja orang yang mencari tidak boleh menjadi orang yang rasional, apa kumpulan pengesahan hati, penghancur gosip, kawalan semula jadi, doktor forensik yang terbaik adalah mencari beberapa orang, orang yang sudah berkahwin, orang lama, pencuri bunga juga perlu mencari, semakin banyak orang yang lebih baik, semakin banyak orang yang lebih baik.

Untuk itu, kita perlu mengambil langkah kedua, bercakap dengan fakta dan bukti. Apakah seorang MM masih bujang atau tidak, kita boleh mencari jawapannya dari banyak perincian.

Seperti melakukan penyelidikan saintifik, anda boleh mencari maklumat terlebih dahulu, carian di google boleh mencari kriteria single yang mudah digunakan yang telah dipelajari oleh banyak orang kesepian selama bertahun-tahun, seperti prinsip telefon bimbit ((anak perempuan yang bercinta menggunakan telefon bimbit lebih kerap), prinsip pembelajaran diri ((anak perempuan yang bujang sering bercinta dengan beberapa anak perempuan).

Ia adalah satu-satunya cara untuk mendapatkan maklumat.

Apabila semua data percubaan siput ini tersedia, kita boleh teruskan, membetulkan dan mengoptimumkan nilai kebarangkalian 65.65% yang baru saja diundi. Bergantung pada apa? Secara semula jadi adalah prestasi gadis sasaran dalam pelbagai kriteria.

Jadi sekarang, peluang untuk sasaran mm menjadi seorang yang bujang akan berubah menjadi

Saya tidak tahu apa-apa, tetapi saya fikir ia akan menjadi lebih baik jika kita teruskan dengan cara yang sama, dan jika kita teruskan dengan cara yang sama.

Jika hasil kajian ini juga mendapati bahawa dalam kalangan gadis bujang, penggunaan telefon bimbit lebih daripada 1.2 kali / jam menyumbang 20%; dalam kalangan gadis yang sudah bercinta, nilai ini adalah 60%. Bagi gadis sasaran, hasil pemerhatian menunjukkan bahawa penggunaan telefon bimbitnya lebih daripada 1.2 kali / jam, maka hasil kebarangkalian perlu diperbaharui

Kemungkinan bujang kembali ke 56.02% dengan cara yang menyedihkan, orang yang rasional boleh mencari lebih banyak kriteria penilaian, melakukan lebih banyak kajian, terus mengemas kini nilai kebarangkalian bujang gadis, supaya ia semakin dekat dengan fakta, tetapi sebelum anda mendapat keputusan akhir, anda harus menetapkan nilai ambang: kemungkinan bujang gadis melebihi nilai ambang ini (misalnya 90%), anda layak untuk menunjukkan tangan anda, jika tidak, anda boleh langsung mati.

Walau bagaimanapun, perlu diingat bahawa tidak kira berapa banyak pengiraan, hasilnya adalah nilai kebarangkalian, bukan fakta, walaupun selepas beberapa kajian, kemungkinan tunggal gadis sasaran dapat ditentukan menjadi 99.9%, dan bersedia untuk mengakuinya, tetapi dalam kajian pemerhatian terakhir terhadap gadis itu, mendapati bahawa orang dan seorang lelaki berjabat tangan dan ketawa, berpelukan bersama, maka, kebarangkalian tunggal gadis akan turun dari 99.9% kepada hampir 0, akibatnya dapat difahami …

Artikel ini memberitahu kita bahawa keputusan ini adalah satu-satunya kaedah sains yang ketat dan rasional yang dikenali sebagai kaedah statistik Bayes. Kaedah Bayes secara ringkasnya adalah bahawa kebarangkalian awal + bukti baru = kebarangkalian yang diperbetulkan.

Walau bagaimanapun, kita tidak boleh mengabaikan Bayesian Theory yang dicipta oleh kaum rasional, yang telah digunakan oleh Tentera Laut Amerika Syarikat untuk mencari bom hidrogen yang hilang dan kapal selam nuklear yang hilang di Lautan Pasifik, dan di bawah ini kita beralih dari saluran emosi ke saluran sejarah.

• ### TWO

Pada suatu hari pada bulan Januari 1966, sebuah pesawat pengebom B-52 Amerika Syarikat terbang di atas Palomares, Sepanyol, beberapa juruterbang di dalam pesawat sedang melaksanakan tugas pengisian minyak udara yang disediakan oleh Komando Tentera Udara mereka. Secara logiknya, penerbangan ini tidak boleh dikatakan berbahaya, dan kaptennya adalah orang yang sangat tenang, tidak suka mengambil dua lubang paip besar, walaupun di dalam kabin pesawat.

Namun, kisah ini tidak berakhir dengan satu lagi siri tragedi dan komedi.

Untuk mencari bom yang hilang itu, Amerika Syarikat segera mengerahkan pasukan pencarian dari dalam negara yang terdiri daripada beberapa pakar ke tempat kejadian, termasuk seorang ahli matematik bernama John Craven, yang bergelar ketua saintis dalam program khas tentera laut Amerika Syarikat.

Cara Craven untuk mencari bom hidrogen menggunakan kaedah Bayesian yang telah disebutkan, dia memanggil pelbagai pakar, tetapi setiap pakar mempunyai bidang kepakaran mereka sendiri, dan tidak mahir. Ada yang tahu banyak tentang pengebom B-52, tetapi sedikit yang diketahui tentang ciri bom hidrogen. Bagaimana bom hidrogen disimpan di pesawat adalah satu masalah, bagaimana bom hidrogen jatuh dari pesawat adalah satu lagi masalah; adakah bom hidrogen akan bersama-sama dengan bangkai pesawat dan tidak ada jawapan; apakah kebarangkalian kedua-dua lubang peluru berpandu pada bom hidrogen masing-masing terbuka?

Craven meminta para pakar untuk membuat pelbagai hipotesis, membayangkan pelbagai senario, dan kemudian meneka kebarangkalian bom hidrogen berada di pelbagai lokasi dalam pelbagai keadaan, dan kemungkinan untuk setiap situasi.

Cara Craven juga dipersoalkan oleh rakan-rakannya, kerana dalam rancangan beliau, banyak hasil yang diperoleh oleh para pakar dalam bentuk dugaan, undi atau boleh dikatakan perjudian, tidak dapat menjamin ketepatan semua hasil, tetapi kerana tugas mencari bom bertenang, tidak ada masa untuk melakukan eksperimen yang tepat, membangunkan teori yang lengkap dan boleh dipercayai, cara Craven tidak dapat dianggap sebagai cara yang boleh dilaksanakan.

Craven mendapat keputusan dari pakar-pakar yang terlibat dalam perundingan untuk mengorbankan seorang wanita, dan mereka semua disatukan untuk membuat peta kemungkinan lokasi bom: ia membahagikan seluruh kawasan yang mungkin menjadi banyak kotak kecil, setiap kotak kecil mempunyai nilai kebarangkalian yang berbeza, yang mempunyai tinggi dan rendah, seperti garis yang sama tinggi yang menunjukkan puncak dan lembah di peta. Seperti ahli-ahli rasional untuk menentukan sama ada seorang gadis masih lajang atau tidak, Craven menyelesaikan langkah pertama kaedah Bayesian.

Craven dan komander pasukan pencarian kemudian memulakan pencarian untuk peluru, mengemas kini kebarangkalian setiap grid pada masa yang sama semasa pencarian, namun, lokasi yang ditunjukkan oleh kotak dengan kebarangkalian terbesar sering kali adalah jurang yang sukar di darat dan kawasan laut dalam, dan walaupun peluru itu benar-benar ada, ia tidak dapat dijumpai, jadi perlu membuat peta kebarangkalian lain yang menunjukkan peluru telah ada di sana, dan kemungkinan yang dapat dijumpai adalah lebih besar daripada kemungkinan lokasi peluru.

Hanya dua tahun kemudian, pada tahun 1968, Craven berpeluang untuk bermain lagi, dan sekali lagi kehilangan peluru serbuk kecil, kali ini Angkatan Laut AS kehilangan peluru serbuk besar.

Pada bulan Jun 1968, kapal selam nuklear Swan milik Tentera Laut hilang secara tiba-tiba di Lautan Pasifik, 99 pegawai dan tentera laut di kapal selam dan bot semuanya tidak dapat didengar. Menurut laporan siasatan selepas kejadian, pelakunya adalah sebuah torpedo yang aneh di kapal selam ini, yang dilancarkan ke luar dan menjadi musuh saya, memutar ke arah dirinya sendiri, menyebabkan peluru dalam kapal selam meletup.

Untuk mencari lokasi Swan, Tentera Laut Amerika Syarikat telah melakukan pencarian besar-besaran, dan Craven juga terlibat. Oleh kerana kelajuan kapal selam yang bergerak perlahan pada masa kemalangan, arah, arah besar kesan letupan, arah arah kapal selam pada masa letupan adalah tidak diketahui, walaupun mengetahui di mana kapal selam meletup, sukar untuk menentukan di mana bangkai kapal selam akhirnya dibanjiri.

Tidak ada pakar yang dapat menganggarkan dengan tepat apa yang berlaku pada kapal selam sebelum dan selepas peristiwa itu, dan seperti ketika mencari peluru serbu, Craven berunding dengan ahli matematik, pakar kapal selam, dan pakar dalam pelbagai bidang pencarian maritim, menulis pelbagai skrip teka-teki yang mungkin, membiarkan mereka membuat perkiraan mengenai arah yang akan berlaku berdasarkan pengetahuan dan pengalaman mereka. Dikatakan, untuk menambah sedikit keseronokan kepada kerja yang membosankan, Craven juga menyediakan balang wiski sebagai hadiah untuk bertaruh yang betul.

Akhirnya, Craven mendapat peta kebarangkalian 20 batu laut. Seluruh kawasan laut dibahagikan kepada banyak grid kecil, setiap grid kecil mempunyai dua nilai kebarangkalian p dan q, p adalah kebarangkalian kapal selam berada di dalam grid ini, q adalah kebarangkalian jika kapal selam berada di dalam grid ini, ia akan dicari.

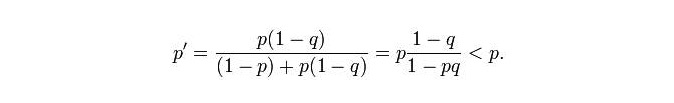
Ini menunjukkan bahawa terdapat kemungkinan yang lebih tinggi untuk kapal selam dari grid lain:

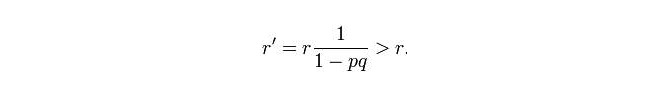
Setiap carian akan memilih satu grid yang mempunyai nilai kebarangkalian tertinggi di seluruh kawasan kapal selam untuk mencari, jika tidak ditemui, carta kebarangkalian akan dibasuh sekali, dan kapal mencari akan menuju ke grid yang paling mencurigakan untuk mencari, dan terus ke bawah, sehingga mencari burung puyuh.

Pada mulanya, pegawai tentera laut dengan pengalaman menganggarkan kapal selam itu berada di dasar laut di sebelah timur tempat letupan, menghiraukan cadangan Craven dan ahli matematik lain, tetapi selepas beberapa bulan pencarian tidak menghasilkan apa-apa. Kemudian tentera laut terpaksa mendengar nasihat Craven, menurut carta kebarangkalian, kapal selam yang terhempas harus berada di sebelah barat tempat letupan. Selepas beberapa kali mencari, kapal selam itu dijumpai di dasar laut barat daya tempat letupan.

Selepas dua persembahan yang kuat, kaedah Bayes yang digunakan oleh Craven dalam pencarian maritim semakin diterima secara meluas, dan sejak itu, kaedah Bayes tidak disangka-sangka menjadi kata kunci di mana-mana bersama-sama dengan bom hidrogen dan kapal selam nuklear. Selama beberapa dekad, kaedah Bayes digunakan secara semakin meluas, dari bar penapis kata carian google hingga kereta tanpa pemandu yang menyeluruh untuk menentukan lokasi pemanduan mereka sendiri.

Dipetik dari Modeling Matematik