Tujuh teknik regresi yang anda patut kuasai

**Artikel ini menerangkan analisis regresi dan kelebihan-kelebihannya, dengan memfokuskan pada tujuh teknik regresi yang paling biasa digunakan dan elemen-elemen kunci yang perlu dikuasai seperti regresi linear, regresi logik, regresi multipolar, regresi bertahap, regresi gelung, regresi runcing, regresi ElasticNet, dan akhirnya faktor-faktor kunci untuk memilih model regresi yang betul. ** ** Analisis regresi butang pengatur adalah alat penting untuk pemodelan dan analisis data. Artikel ini menerangkan makna dan kelebihan analisis regresi, dengan fokus meringkaskan tujuh teknik regresi yang paling biasa digunakan dan elemen-elemen kunci untuk memilih model regresi yang betul, seperti regresi linear, regresi logik, regresi multipolar, regresi bertahap, regresi gelung, regresi runcing, dan regresi ElasticNet.**

• ### Apakah analisis regresi?

Analisis regresi adalah teknik pemodelan ramalan yang mengkaji hubungan antara pembolehubah sebab (target) dan pembolehubah diri (proklamator). Teknik ini biasanya digunakan dalam analisis ramalan, model urutan masa, dan hubungan sebab-akibat antara pembolehubah yang ditemui. Sebagai contoh, hubungan antara pemandu yang tidak bertanggungjawab dan jumlah kemalangan jalan raya, kaedah terbaik untuk mengkaji adalah regresi.

Analisis regresi adalah alat penting untuk memodelkan dan menganalisis data. Di sini, kita menggunakan kurva/garis untuk menyesuaikan titik data ini, dengan cara ini, perbezaan jarak dari kurva atau garis ke titik data adalah minimum. Saya akan menerangkannya dengan terperinci dalam bahagian seterusnya.

• ### Mengapa kita menggunakan analisis regresi?

Analisis regresi menganggarkan hubungan antara dua atau lebih pembolehubah, seperti yang dinyatakan di atas. Di bawah ini, mari kita ambil contoh mudah untuk memahaminya:

Sebagai contoh, dalam keadaan ekonomi semasa, anda perlu menganggarkan pertumbuhan jualan sebuah syarikat. Sekarang, anda mempunyai data terkini syarikat yang menunjukkan bahawa pertumbuhan jualan adalah kira-kira 2.5 kali ganda pertumbuhan ekonomi. Kemudian menggunakan analisis regresi, kita boleh menggunakan maklumat semasa dan masa lalu untuk meramalkan jualan masa depan syarikat.

Terdapat banyak faedah menggunakan analisis regresi:

Ia menunjukkan hubungan yang ketara antara pembolehubah dan pembolehubah;

Ia menunjukkan intensiti kesan pelbagai pembolehubah terhadap pembolehubah penyebab.

Analisis regresi juga membolehkan kita membandingkan kesan antara pembolehubah yang mengukur skala yang berbeza, seperti hubungan antara perubahan harga dan jumlah aktiviti promosi. Ini membantu penyelidik pasaran, penganalisis data, dan saintis data untuk mengecualikan dan menganggarkan satu set pembolehubah terbaik untuk membina model ramalan.

• ### Berapa banyak teknik regresi yang kita ada?

Terdapat pelbagai teknik regresi yang digunakan untuk membuat ramalan. Teknik-teknik ini mempunyai tiga ukuran utama: bilangan pelarut, jenis pelarut, dan bentuk garis regresi. Kami akan membincangkannya secara terperinci dalam bahagian berikut.

Bagi mereka yang kreatif, anda boleh membuat model regresi yang tidak pernah digunakan jika anda merasa perlu menggunakan kombinasi parameter di atas. Tetapi sebelum anda memulakan, ketahui kaedah regresi yang paling biasa:

• 1. Regresi Linear

  Ia adalah salah satu teknik pemodelan yang paling terkenal. Regresen linear biasanya merupakan salah satu teknik yang dipilih oleh orang ramai ketika mempelajari model ramalan. Dalam teknik ini, kerana pembolehubah adalah berturut-turut, pembolehubah sendiri boleh berturut-turut atau terpisah, sifat garis regresen adalah linear.

  Regresen linear menggunakan garis lurus penyesuaian terbaik ((iaitu garis regresi) untuk mewujudkan hubungan antara pembolehubah akibat ((Y) dan satu atau lebih pembolehubah diri ((X)).

  Ia boleh dirujuk dengan persamaan Y=a+b.*X + e, di mana a mewakili jarak, b mewakili kecenderungan garis lurus, dan e adalah titik kesilapan. Persamaan ini boleh meramalkan nilai pembolehubah sasaran berdasarkan pembolehubah ramalan yang diberikan (s).

  

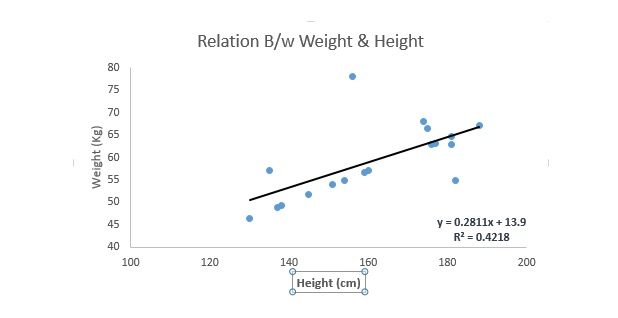
  Perbezaan antara regresi unilinear dan regresi multilinear ialah regresi multilinear mempunyai ((>1) pembolehubah, manakala regresi unilinear biasanya hanya mempunyai 1 pembolehubah. Persoalannya sekarang ialah bagaimana kita mendapatkan garis penyesuaian yang optimum?

  Bagaimana untuk mendapatkan nilai-nilai yang paling sesuai (a dan b)?

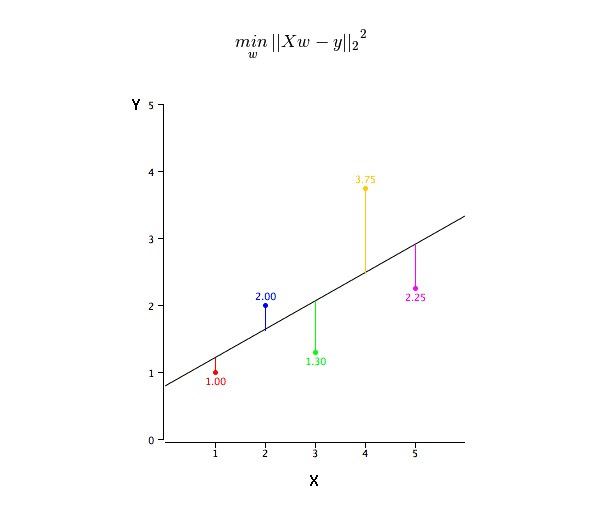
  Masalah ini dapat dilakukan dengan mudah dengan menggunakan penggandaan dua terendah. Penggandaan dua terendah juga merupakan kaedah yang paling biasa digunakan untuk menyesuaikan garis regresi. Untuk data pemerhatian, ia mengira garis penyesuaian terbaik dengan meminimumkan jumlah kuadrat penyimpangan menegak setiap titik data ke garis.

  

  Kita boleh menggunakan R-square metrik untuk menilai prestasi model. Untuk maklumat lanjut mengenai metrik ini, baca: Metrik Prestasi Model Part 1, Part 2 .

  Maksudnya:

  • Terdapat hubungan linear antara pembolehubah dan pembolehubah faktor
  • Kembalian berbilang mempunyai banyak ko-lineariti, korelasi diri, dan kecacatan.
  • Regresi linear sangat sensitif terhadap nilai luar biasa. Ia akan menjejaskan garis regresi dan akhirnya mempengaruhi nilai ramalan.
  • Komponen-komponen ini akan meningkatkan perbezaan dalam nilai-nilai pengiraan faktor, menjadikan pengiraan sangat sensitif dengan perubahan kecil dalam model. Akibatnya, pengiraan faktor tidak stabil.
  • Dalam kes pelbagai pembolehubah diri, kita boleh menggunakan kaedah pemilihan ke hadapan, kaedah penyingkiran ke belakang dan kaedah penyaringan beransur-ansur untuk memilih pembolehubah diri yang paling penting.

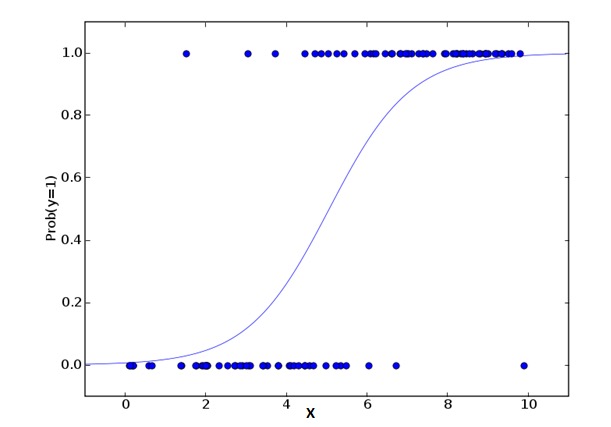
• 2. Regression Logistik

  Regresen logik digunakan untuk mengira kebarangkalian peristiwa bertepatan =Success dan peristiwa bertepatan =Failure. Kita harus menggunakan regresen logik apabila jenis pembolehubah adalah pembolehubah binari ((¹⁄₀, benar/palsu, ya/tidak). Di sini, nilai Y adalah dari 0 hingga 1, yang boleh dinyatakan dengan persamaan berikut:

  odds= p/ (1-p) = probability of event occurrence / probability of not event occurrence
  ln(odds) = ln(p/(1-p))
  logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3....+bkXk
  

  Dalam formula di atas, p menyatakan kebarangkalian mempunyai ciri-ciri tertentu. Anda sepatutnya bertanya soalan ini: Oh, mengapa kita menggunakan log log dalam formula? Oh.

  Kerana di sini kita menggunakan sebaran binomial ((variabel), kita perlu memilih satu fungsi penghubung yang terbaik untuk sebaran ini. Ia adalah fungsi Logit. Dalam persamaan di atas, parameter dipilih dengan mengamati sampel yang sangat berkemungkinan untuk menganggarkan nilai, dan bukannya meminimumkan kuasa dua dan kesilapan (seperti yang digunakan dalam Regression Biasa).

  

  Maksudnya:

  • Ia digunakan secara meluas untuk soalan klasifikasi.
  • Regresen logik tidak memerlukan pembolehubah diri dan pembolehubah faktor untuk menjadi hubungan linear. Ia boleh menangani pelbagai jenis hubungan kerana ia menggunakan penukaran logik yang tidak linear terhadap Indeks Risiko Relatif OR yang diramalkan.
  • Untuk mengelakkan overfit dan underfit, kita harus memasukkan semua pembolehubah yang penting. Terdapat cara yang baik untuk memastikan ini adalah dengan menggunakan kaedah penyaringan beransur-ansur untuk menganggarkan pulangan logik.
  • Ia memerlukan jumlah sampel yang besar, kerana dalam jumlah sampel yang lebih kecil, kebarangkalian yang sangat besar menganggarkan kesan yang lebih buruk daripada yang biasa.
  • Variabel-variabel itu sendiri tidak sepatutnya saling berkaitan, iaitu tidak mempunyai kepelbagaian ko-linier. Walau bagaimanapun, dalam analisis dan pemodelan, kita boleh memilih untuk memasukkan kesan interaksi pembolehubah klasifikasi.
  • Jika nilai pemboleh ubah adalah pemboleh ubah susunan, ia dipanggil pengembalian logik susunan.
  • Jika ia berbilang jenis, ia dipanggil regresi logik berbilang.

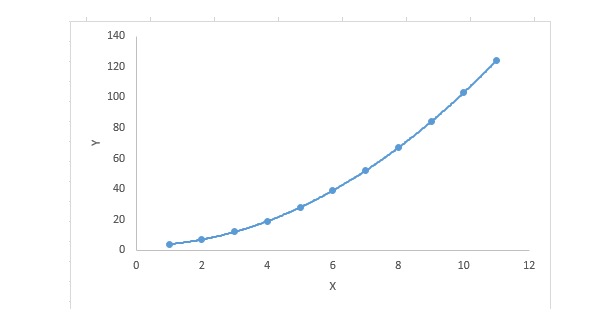
• 3. Regression Polynomial

  Untuk persamaan regresi, jika indeks pembolehubah sendiri lebih besar daripada 1, maka ia adalah persamaan regresi polinomial. Persamaan berikut ditunjukkan:

  y=a+b*x^2
  

  Dalam teknik regresi ini, garis penyesuaian yang terbaik bukanlah garis lurus. Ia adalah satu keluk yang digunakan untuk penyesuaian titik data.

  

  Penekanan:

  • Walaupun terdapat satu induksi yang boleh memadankan satu polinomial peringkat tinggi dan mendapat kesilapan yang lebih rendah, ia boleh menyebabkan overfit. Anda perlu kerap melukis carta hubungan untuk melihat keadaan yang sesuai, dan memberi tumpuan kepada memastikan bahawa yang sesuai adalah wajar, tidak ada overfit dan tidak ada kurang sesuai. Berikut adalah satu grafik yang boleh membantu memahami:

  

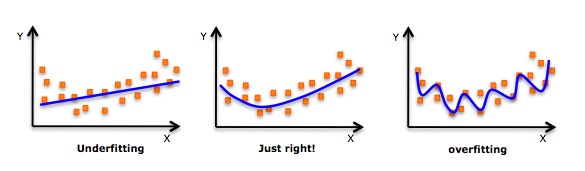
  • Jelas mencari titik-titik pada kedua-dua hujung keluk untuk melihat apakah bentuk dan trend ini masuk akal.

• 4. Regressi Langkah demi langkah

  Dalam teknik ini, pemilihan pembolehubah dilakukan dalam proses automatik, termasuk operasi bukan manusia.

  Kejayaan ini adalah untuk mengenal pasti pembolehubah penting dengan melihat nilai statistik seperti R-square, t-stats dan AIC. Regresen beransur-ansur menyesuaikan model dengan menambah / menghapuskan pembolehubah bersama berdasarkan piawaian yang ditetapkan. Berikut adalah beberapa kaedah regresen beransur-ansur yang paling biasa digunakan:

  • Regresi beransur-ansur standard melakukan dua perkara: menambah dan mengurangkan ramalan yang diperlukan untuk setiap langkah.
  • Pemilihan ke hadapan bermula dengan ramalan yang paling ketara dalam model dan kemudian menambah pembolehubah untuk setiap langkah.
  • Penghapusan ke belakang bermula pada masa yang sama dengan semua ramalan model, dan kemudian menghilangkan pembolehubah yang paling tidak ketara pada setiap langkah.
  • Teknik pemodelan ini bertujuan untuk memaksimumkan kebolehan ramalan dengan menggunakan bilangan pembolehubah ramalan yang minimum. Ia juga merupakan salah satu kaedah untuk menangani set data berdimensi tinggi.

• 5. Ridge Regression

  Analisis regresi berlian adalah satu teknik yang digunakan untuk data yang mempunyai banyak komorbiditi. Dalam keadaan yang banyak komorbiditi, walaupun penggandaan minimum (OLS) adalah adil untuk setiap pembolehubah, perbezaan mereka sangat besar, menyebabkan nilai pengamatan menyimpang dan jauh dari nilai sebenar. Regresi berlian mengurangkan kesilapan piawai dengan menambah satu bias pada anggaran regresi yang diberikan.

  Di atas, kita melihat persamaan regresi linear. Ingat? Ia boleh dinyatakan sebagai:

  y=a+ b*x
  

  Persamaan ini juga mempunyai satu kesalahan. Persamaan lengkapnya ialah:

  y=a+b*x+e (error term),  [error term is the value needed to correct for a prediction error between the observed and predicted value]
  => y=a+y= a+ b1x1+ b2x2+....+e, for multiple independent variables.
  

  Dalam persamaan linear, kesilapan ramalan boleh dipecah menjadi 2 subpartikel. Salah satu adalah bias dan satu adalah perbezaan. Kesalahan ramalan mungkin disebabkan oleh kedua-dua faktor atau salah satu daripadanya. Di sini, kita akan membincangkan mengenai kesilapan yang disebabkan oleh perbezaan.

  Pengembalian berlian menyelesaikan masalah komalineriti berganda dengan parameter pengurangan λ ((lambda)). Lihat formula di bawah

  

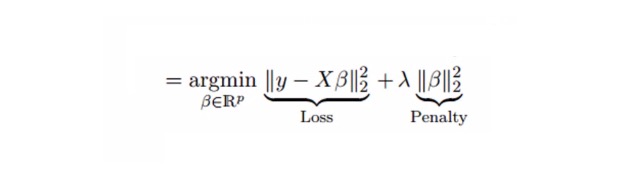
  Dalam formula ini, terdapat dua komponen. Yang pertama adalah binomial terkecil, dan yang lain adalah kelipatan λ dari β2 ((β-squared), di mana β adalah faktor yang berkaitan. Untuk meringkaskan parameter, tambahkannya ke dalam binomial terkecil untuk mendapatkan perbezaan yang sangat rendah.

  Maksudnya:

  • Dengan pengecualian nombor senantiasa, hipotesis regresi ini serupa dengan regresi binomial terkecil;
  • Ia mengecilkan nilai faktor yang berkaitan tetapi tidak mencapai sifar, yang menunjukkan bahawa ia tidak mempunyai ciri-ciri pilihan
  • Ini adalah kaedah pengaturan dan menggunakan pengaturan L2.

• 6. Lasso Regression

  Ianya serupa dengan pengurangan berlian, Lasso (Least Absolute Shrinkage and Selection Operator) juga menghukum saiz mutlak faktor pengurangan. Selain itu, ia dapat mengurangkan tahap perubahan dan meningkatkan ketepatan model pengurangan linear. Lihat formula di bawah:

  

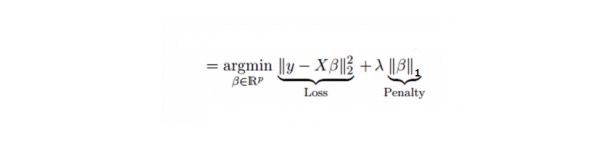
  Regresen Lasso sedikit berbeza dengan Regresen Ridge, ia menggunakan fungsi hukuman sebagai nilai mutlak dan bukannya kuasa dua. Ini menyebabkan hukuman (atau sama dengan jumlah nilai mutlak yang diikat) membuat beberapa parameter yang dianggarkan sama dengan sifar.

  Maksudnya:

  • Dengan pengecualian nombor senantiasa, hipotesis regresi ini serupa dengan regresi binomial terkecil;
  • Koefisien penyusutan hampir sifar ((sama dengan sifar), yang memang membantu pemilihan ciri;
  • Ini adalah kaedah penyesuaian yang menggunakan penyesuaian L1;
  • Jika satu set pembolehubah yang diramalkan adalah sangat berkaitan, Lasso akan memilih salah satu daripada pembolehubah tersebut dan mengurangkan yang lain kepada sifar.

• 7. Kembali ke ElasticNet

  ElasticNet adalah campuran antara Lasso dan teknik Regression Ridge. Ia menggunakan L1 untuk latihan dan L2 sebagai matriks penyesuaian. ElasticNet berguna apabila terdapat beberapa ciri yang berkaitan. Lasso akan memilih salah satu daripada mereka secara rawak, manakala ElasticNet akan memilih dua.

  

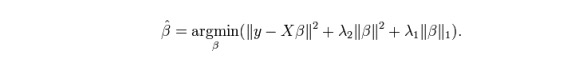
  Kelebihan praktikal antara Lasso dan Ridge adalah bahawa ia membolehkan ElasticNet mewarisi beberapa kestabilan Ridge dalam keadaan pusing.

  Maksudnya:

  • Dalam kes-kes yang sangat berkaitan, ia akan menghasilkan kesan kumpulan.
  • Tidak ada had kepada bilangan pembolehubah yang boleh dipilih.
  • Ia boleh tahan dua kali pengecutan.
  • Selain daripada 7 teknik regresi yang paling biasa digunakan, anda boleh melihat model lain seperti regresi Bayesian, Ekologi dan Robust.

• Bagaimana untuk memilih model regresi yang betul?

  Kehidupan biasanya lebih mudah apabila anda hanya tahu satu atau dua teknik. Satu institusi latihan yang saya tahu memberitahu pelajar mereka bahawa jika hasilnya adalah berturut-turut, gunakan regresi linear. Jika ia adalah binari, gunakan regresi logik.

  Dalam model regresi pelbagai jenis, sangat penting untuk memilih teknik yang paling sesuai berdasarkan jenis pembolehubah dan pembolehubah faktor, dimensi data, dan ciri asas lain data. Berikut adalah faktor penting untuk memilih model regresi yang betul:

  Penjelajahan data adalah bahagian penting dalam membina model ramalan. Ia harus menjadi langkah utama dalam memilih model yang sesuai, seperti mengenal pasti hubungan dan pengaruh pembolehubah.

  Lebih sesuai dengan kelebihan model yang berbeza, kita boleh menganalisis parameter penunjuk yang berbeza, seperti parameter yang bermakna secara statistik, R-square, Adjusted R-square, AIC, BIC, dan titik kesilapan, dan yang lain adalah peraturan Mallows’ Cp. Ini dilakukan terutamanya dengan membandingkan model dengan semua submodel yang mungkin (atau memilihnya dengan berhati-hati), memeriksa kemungkinan penyimpangan dalam model anda.

  Penyelesaian silang adalah kaedah terbaik untuk menilai model ramalan. Di sini, bahagikan set data anda kepada dua bahagian (satu untuk latihan dan satu untuk pengesahan). Gunakan perbezaan rata sederhana antara nilai pemerhatian dan nilai ramalan untuk mengukur ketepatan ramalan anda.

  Jika anda mempunyai set data dengan pelbagai pembolehubah campuran, anda tidak boleh memilih kaedah pemilihan model automatik, kerana anda tidak mahu meletakkan semua pembolehubah dalam model yang sama pada masa yang sama.

  Ia juga bergantung kepada tujuan anda. Ia mungkin berlaku bahawa model yang kurang kuat lebih mudah dilaksanakan berbanding model yang mempunyai makna statistik yang tinggi.

  Kaedah regresi normalisasi ((Lasso, Ridge dan ElasticNet) berfungsi dengan baik dalam keadaan komutatif berganda antara variabel set data berdimensi tinggi.

Dipetik dari CSDN