Pemahaman Menarik tentang Naive Bayes

NavieBayes

  Banyak situasi dalam kehidupan memerlukan pengelompokan, seperti pengelompokan berita, pengelompokan pesakit, dan lain-lain. Untuk memberi pemahaman kepada anda, artikel ini memperkenalkan algoritma pengelompokan yang mudah dan biasa digunakan dari aplikasi praktikal - Bayes polos (Navie Bayes classifier).

• 01 Contoh klasifikasi pesakit

Saya akan mulakan dengan satu contoh, anda akan melihat bahawa klasifikasi Bayesian sangat mudah difahami, tidak sukar. Satu hospital menerima enam pesakit rawat jalan di pagi hari, seperti yang ditunjukkan oleh jadual di bawah.

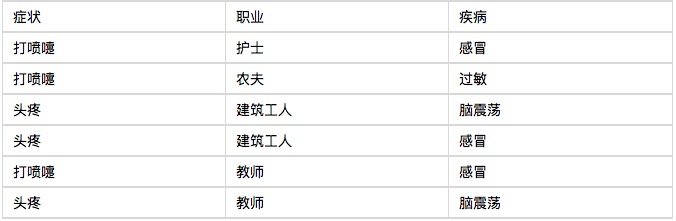
Sekarang datang pesakit ketujuh, seorang pekerja binaan yang bersin. Berapakah kebarangkalian dia terkena selesema?

  P(A|B) = P(B|A) P(A) / P(B)

Bolehkah:

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏x建筑工人|感冒) x P(感冒) 
  　　　　/ P(打喷嚏x建筑工人)

Dengan mengandaikan bahawa ciri-ciri “menyedut” dan “pekerja binaan” adalah berasingan, maka persamaan di atas menjadi

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒)
  　　　　/ P(打喷嚏) x P(建筑工人)

Ia boleh dikira.

  P(感冒|打喷嚏x建筑工人) 
  　　　　= 0.66 x 0.33 x 0.5 / 0.5 x 0.33 
  　　　　= 0.66

Oleh itu, pekerja binaan yang bersin itu mempunyai kemungkinan 66% mendapat selesema. Dengan cara yang sama, kemungkinan pesakit mengalami alahan atau gegaran otak dapat dikira. Dengan membandingkan kemungkinan ini, anda dapat mengetahui penyakit yang paling mungkin dia dapat.

Ini adalah kaedah asas bagi pengelompokan Bayesian: berdasarkan data statistik, berdasarkan ciri-ciri tertentu, kira kebarangkalian bagi setiap kategori, untuk mencapai pengelompokan.

• 02 Rumus bagi klasifikator Bayes sederhana

Anggap seseorang mempunyai n ciri, iaitu F1, F2, … dan Fn. Terdapat m kategori, iaitu C1, C2, … dan Cm. Klasifikator Bayesian adalah klasifikasi yang paling berkemungkinan, iaitu nilai maksimum formula berikut:

  P(C|F1F2...Fn) 
  　　   = P(F1F2...Fn|C)P(C) / P(F1F2...Fn)

Oleh kerana P ((F1F2…Fn) adalah sama untuk semua kategori, ia boleh diabaikan, dan soalan akan berubah menjadi

  P(F1F2...Fn|C)P(C)

Nilai maksimum

Klasifikator Bayesian yang sederhana mengambil langkah lebih jauh, dengan mengandaikan bahawa semua ciri-ciri adalah berasingan antara satu sama lain, dan oleh itu

  P(F1F2...Fn|C)P(C) 
  　　   = P(F1|C)P(F2|C) ... P(Fn|C)P(C)

Setiap elemen di sebelah kanan persamaan dapat diperoleh dari statistik, dan dengan itu kemungkinan yang sesuai untuk setiap kategori dapat dikira, dan dengan itu dapat dijumpai kelas yang mempunyai kebarangkalian terbesar.

Walaupun hipotesis bahawa “semua ciri-ciri adalah bebas dari satu sama lain” tidak mungkin berlaku dalam realiti, ia dapat mempermudahkan pengiraan secara besar-besaran, dan kajian menunjukkan sedikit kesan terhadap ketepatan hasil klasifikasi.

Berikut adalah dua contoh untuk melihat bagaimana menggunakan pengelasan Bayes sederhana.

• 03 Pengelompokan akaun

Berdasarkan statistik sampel dari laman web komuniti, 89% daripada 10,000 akaun adalah akaun sebenar (set C0) dan 11% adalah akaun palsu (set C1). Kemudian, anda perlu menggunakan statistik untuk menilai keaslian akaun.

  C0 = 0.89 C1 = 0.11

Anggaplah satu akaun mempunyai tiga ciri berikut: F1: Bilangan hari di dalam jurnal F2: Bilangan kawan/hari pendaftaran F3: Apakah menggunakan imej sebenar (imaj sebenar ialah 1, imej bukan sebenar ialah 0) F1 = 0.1  F2 = 0.2  F3 = 0

Adakah akaun itu benar atau palsu? Cara menggunakan pengelasan Bayes sederhana untuk mengira nilai formula di bawah ini:

P(F1|C)P(F2|C)P(F3|C)P©

Walaupun nilai-nilai di atas boleh diperolehi dari statistik, tetapi ada masalah di sini: F1 dan F2 adalah pembolehubah berturut-turut, dan tidak sesuai untuk mengira kebarangkalian mengikut nilai tertentu. Satu teknik adalah menukar nilai berturut-turut menjadi nilai buas, untuk mengira kebarangkalian antara.[0, 0.05]、(0.05, 0.2)、[0.2, +∞] tiga julat, dan kemudian mengira kebarangkalian setiap julat. Dalam contoh kita, F1 adalah 0.1, jatuh di julat kedua, jadi kiraan menggunakan kebarangkalian julat kedua.

Menurut statistik, ia boleh didapati:

P(F1|C0) = 0.5, P(F1|C1) = 0.1  P(F2|C0) = 0.7, P(F2|C1) = 0.2  P(F3|C0) = 0.2, P(F3|C1) = 0.9

Oleh itu,

P(F1|C0) P(F2|C0) P(F3|C0) P(C0)  = 0.5 x 0.7 x 0.2 x 0.89  = 0.0623 P(F1|C1) P(F2|C1) P(F3|C1) P(C1)  = 0.1 x 0.2 x 0.9 x 0.11  = 0.00198 Anda dapat melihat bahawa walaupun pengguna ini tidak menggunakan imej wajah sebenar, kemungkinan bahawa dia adalah akaun sebenar adalah lebih dari 30 kali lebih tinggi daripada akaun palsu, dan oleh itu ia dianggap sebagai akaun sebenar.

• 04 Pengelompokan jantina

Berikut adalah statistik mengenai ciri-ciri tubuh manusia.

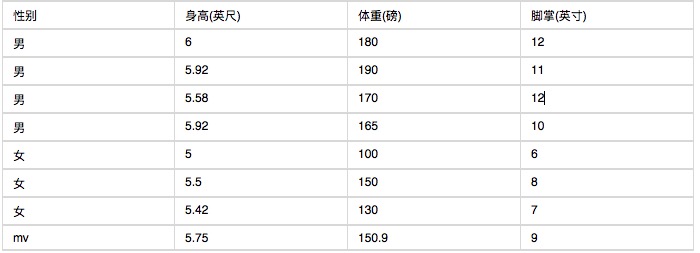
Jika seseorang diketahui mempunyai tinggi 6 kaki, berat 130 paun, dan telapak kaki 8 inci, adakah ia lelaki atau perempuan?

P (Tinggian) x P (Badan) x P (Seks)

Masalahnya ialah, kerana tinggi badan, berat badan, dan tapak kaki adalah pembolehubah berturut-turut, kemungkinan tidak dapat dikira dengan menggunakan kaedah pembolehubah bersendirian. Dan kerana sampel terlalu sedikit, kemungkinan tidak dapat dikira secara berselang-seling. Apa yang perlu dilakukan?

Dengan data ini, anda boleh mengira klasifikasi jantina.

P (tinggi = 6 orang lelaki) x P (berat = 130 orang lelaki) x P (tangan = 8 orang lelaki) x P (lelaki)

= 6.1984 x e-9

P (tinggi = 6 darab) x P (berat = 130 darab) x P (tangan = 8 darab) x P (perempuan)

= 5.3778 x e-4

Di sini, kita dapat melihat bahawa wanita adalah hampir 10,000 kali lebih mungkin daripada lelaki, jadi ia adalah wanita.

Diambil dari laman WeChat Public Number yang diunggah oleh Weibo