Pemahaman Intuitif Mengenai Kointegrasi

Petunjuk: Artikel ini bertujuan untuk memperkenalkan konsep integrasi secara intuitif, membantu anda memahami makna asasnya, motif konsep ini, dan senario aplikasi yang mudah.

• Penerangan

Di sini saya hanya ingin menunjukkan kepada anda definisi intuitif integrasi, dan tidak melibatkan definisi simbol matematik yang ketat dan penarikan formula yang ketat.

Jika anda berminat, boleh rujuk: Wikipedia Cointegration.

Kenapa perlu bersatu?

“Saya tidak tahu apa-apa tentang ini, saya tidak tahu apa-apa tentang ini, saya tidak tahu apa-apa tentang ini.

Secara ringkasnya, kestabilan (atau stationarity) adalah sifat urutan yang kekal stabil dan tidak berubah dari masa ke masa, dan ia adalah sifat yang sangat kita sukai ketika melakukan ramalan analisis data. Jika sekumpulan data urutan masa stabil, itu bermakna nilai rata-rata dan perbezaan tidak berubah, sehingga kita dapat menggunakan beberapa teknik statistik dengan mudah pada urutan.

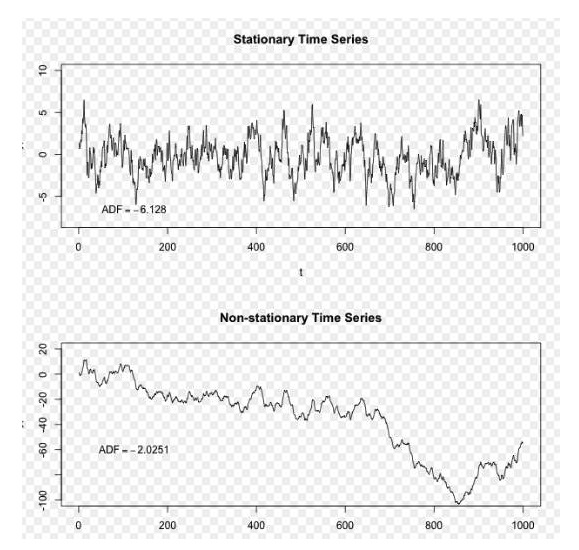
Sumber gambar: Wikipedia

Dalam rajah di atas, urutan di atas adalah urutan yang seimbang, dan kita dapat melihat bahawa ia sentiasa bergelombang di sekitar purata jangka panjang, dan urutan di bawah adalah urutan yang tidak seimbang, dan kita dapat melihat bahawa purata jangka panjangnya berubah-ubah.

Sebagai contoh aplikasi, jika urutan harga suatu aset (atau perbezaan harga antara dua urutan) adalah stabil, maka apabila ia menyimpang dari nilai purata, seseorang boleh mengharapkan harga akan kembali ke nilai purata pada suatu masa di masa depan. Kita boleh menggunakan sifat ini untuk melabur dan mendapat keuntungan.

Ini adalah urutan harga saham yang stabil:

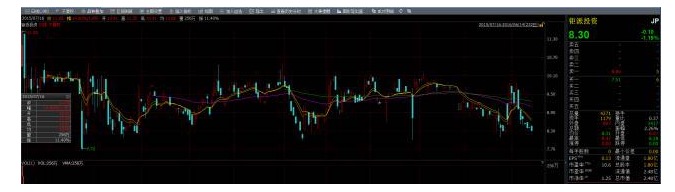
Jika dua kumpulan urutan tidak stabil, tetapi kombinasi linear mereka dapat menghasilkan urutan yang stabil, maka kita boleh mengatakan bahawa kedua-dua kumpulan data urutan masa mempunyai sifat yang seimbang, dan kita juga boleh menggunakan sifat statistik pada urutan gabungan ini. Tetapi perlu diperhatikan bahawa hubungan seimbang bukanlah hubungan yang berkaitan.

Sebagai contoh, jika perbezaan antara dua set data siri masa adalah seimbang, kita boleh membuat keuntungan dengan pelaburan berdasarkan keseimbangan perbezaan ini: apabila harga dua saham terlalu jauh, berdasarkan keseimbangan kita menjangkakan perbezaan harga akan berdekatan, jadi membeli saham dengan harga rendah, menjual saham dengan harga tinggi, dan melakukan operasi terbalik sambil menunggu harga kembali sehingga mendapat keuntungan.

Itulah asal usul pairs trading. Adakah ia jelas?

• Kestabilan dan kaedah ujian

Secara ketat, kestabilan boleh dibahagikan kepada kestabilan yang ketat dan kestabilan yang lemah. Kestabilan yang ketat bermaksud bahawa urutan selalu mempunyai fungsi pengedaran yang tidak berubah, dan kestabilan lemah bermaksud bahawa urutan mempunyai jumlah statistik deskriptif yang tetap. Semua urutan kestabilan yang kuat memenuhi sifat kestabilan yang lemah, tetapi sebaliknya tidak berlaku.

Contoh aplikasi

Pertama sekali, perlu diperhatikan bahawa hubungan kohesi bukanlah hubungan yang berkaitan. Kita membina dua set data secara buatan, dan dengan itu melihat hubungan kohesi secara intuitif. import numpy as np import pandas as pd import seaborn import statsmodels import matplotlib.pyplot as plt from statsmodels.tsa.stattools import coint

Data pembinaan

Pertama, kita membina dua set data, setiap set data mempunyai panjang 100 . Kumpulan data pertama adalah 100 ditambah satu item trend ke bawah ditambah satu peredaran normal standard . Kumpulan data kedua adalah berdasarkan kumpulan data pertama ditambah 30, ditambah satu peredaran normal standard tambahan .

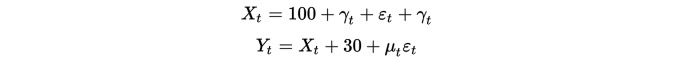
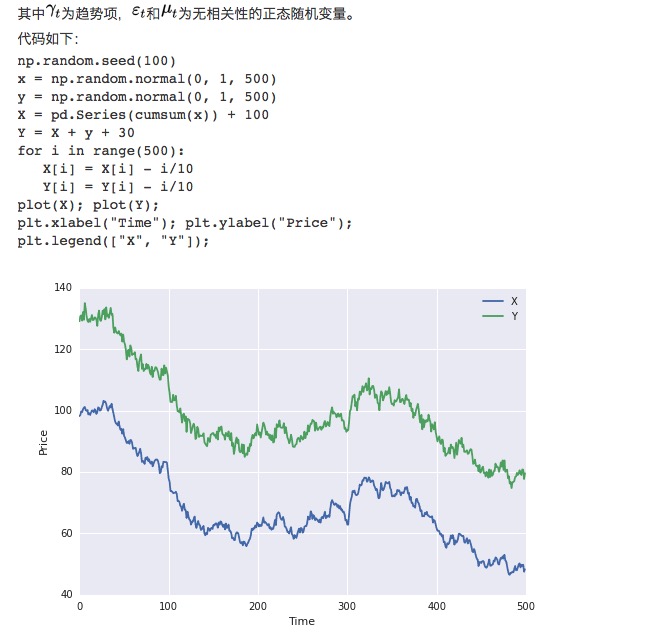
Jelas sekali, kedua-dua set data ini tidak seimbang, kerana nilai purata berubah mengikut perubahan masa. Tetapi kedua-dua set data ini mempunyai hubungan integrasi, kerana urutan perbezaan mereka seimbang:

plot(Y-X); plt.axhline((Y-X).mean(),color=“red”, linestyle=“–”); plt.xlabel(“Time”); plt.ylabel(“Price”); plt.legend([“Y-X”, “Mean”]);

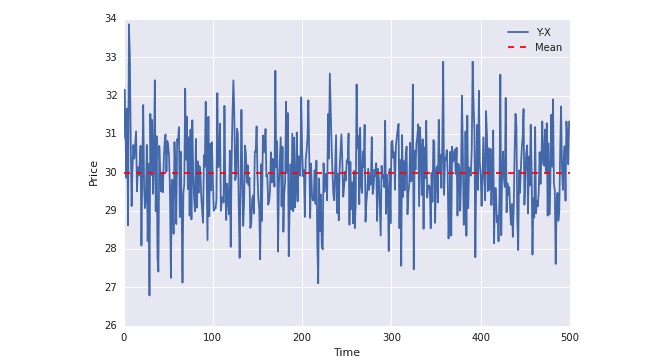
Dalam gambar di atas, dapat dilihat bahawa garis biru sentiasa bergelombang di sekitar nilai purata. Nilai purata tidak berubah mengikut masa.

• Penutup

Jika anda bercakap tentang integrasi dari sudut matematik, ia akan menjadi lebih rumit, dan kelas kuantitatif akan terlibat di kemudian hari. Kami hanya membuat pengenalan ringkas pada tahap pengertian (level-0) untuk membolehkan anda menggabungkan integrasi dengan aplikasi sebenar.

Berkongsi, Bertukar dari Kelas Kuantitatif