风险小史 (四) 莫弗与神曲线

Dalam edisi yang lalu, Jacob Bernoulli berkata bahawa pada masa kematiannya, dia belum menerbitkan buku-bukunya mengenai teori kebarangkalian. Tugas menyusun manuskripnya diserahkan kepada keponakannya, Nicholas II Bernoulli (genius yang lebih awal). Setelah menyelesaikan wasiat pamannya, Nicholas mula ingin meneliti tahap penyimpangan kebarangkalian sebenar dengan jumlah pemerhatian yang telah ditentukan. Di banyak tempat, Moivre (Abraham de Moivre) diterjemahkan sebagai Moivre, tetapi selepas melihat gambarnya, saya tidak begitu menyokong terjemahan ini. Ia adalah satu tawaran yang boleh mencapai satu kisah yang terkenal di dunia akhirat, tetapi Moivre menolaknya. Dan dia menolaknya kerana dia merasakan dia tidak cukup kuat.

• Dunmow Dia sebenarnya hanya berusia 13 tahun lebih muda daripada Jacob Bernoulli, dan seluruh hidupnya sebenarnya dapat digambarkan dalam sebuah novel, iaitu The Tragic World of Joan of Arc. Pada masa itu, Perancis adalah sebuah negara yang mempunyai suasana Katolik yang fanatik, dan Joan of Arc mungkin atau mungkin bukan seorang Protestan. Kemudian, Raja Louis XIV dari Perancis mengeluarkan undang-undang yang mengisytiharkan orang Protestan di negara itu sebagai warganegara yang lebih rendah, dan anak-anak kecil harus bertukar menjadi Protestan, yang pada dasarnya menjadikan Protestan sebagai kultus di Perancis, dan Joan of Arc dipenjarakan selama dua tahun.

Tetapi kita masih harus berseru di sini, Yang Morpheus tidak akan mati! Pada tahun 1711, Yang Morpheus menerbitkan sebuah buku tentang ukuran keberuntungan, Yang Morpheus, dan jika buku itu diterbitkan pada masa itu, ia pasti mempunyai sampul pinggang yang ditulis di atas sampul pinggangnya dengan kata-kata Newton yang disyorkan:

Namun tidak pada masa itu, jadi Don Moffat tidak dapat mengumpul banyak cukai.

Anda mungkin masih ingat soalan yang kita bincangkan dalam artikel sebelumnya (Risiko 3: Encik Bernoulli), untuk 5000 batu kerikil dalam tong, kita boleh melakukan 25,500 penggambaran untuk menganggarkan perkadaran keseluruhan batu kerikil. Tetapi anda mungkin juga dapat mengetahui bahawa 25,500 penggambaran berulang adalah terlalu banyak, lebih baik daripada membuang batu itu satu satu.

Dengan menggunakan kaedah kalkulus dan segitiga Pascal, Dunmore menggunakan kaedah pengambilan kumpulan. Ia menganggap bahawa 100 batu kerikil diambil dari kandang pada setiap kali, mencatat perkadaran batu kerikil hitam dan putih, meletakkan batu itu kembali, dan melakukan pengambilan yang sama. Dengan cara ini, Dunmore dapat memberitahu anda lebih awal tentang perbandingan yang anda catat dan perkadaran yang hampir sama dengan perkadaran sebenar, dan bagaimana perkadaran ini diedarkan di sekitar nilai purata mereka.

Apakah ungkapan ini seperti biasa, atau adakah perasaan itu berada di mulut anda, atau adakah anda ingin memanggilnya dengan nama itu? Ya, ini adalah peredaran normal yang kita semua kenal. Garis lurus peredaran normal adalah seperti kurva berbentuk bel, di mana kebanyakan nilai pemerhatian berkumpul di tengah, mendekati rata-rata semua nilai pemerhatian, dan kemudian bersandar secara simetrik ke kedua-dua hujungnya dari arah rata-rata, dan jumlah nilai pemerhatian di kedua-dua hujungnya adalah sama.

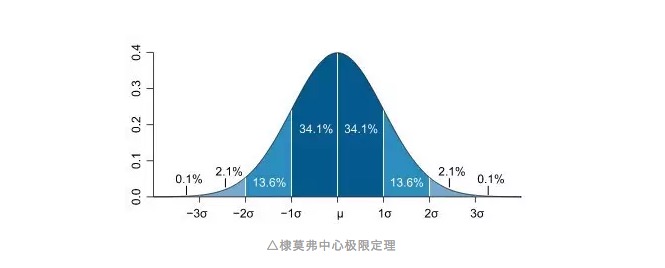
Dengan cara ini kita boleh memperkenalkan konsep standard deviation, sebenarnya dalam artikel lain dalam Jurnal Publik (Why standard deviation? Measurement of risk in the eyes of God) kita telah menyebutnya. Standard deviation sebenarnya menggambarkan sejauh mana nilai pemerhatian menyimpang dari nilai purata, atau kita memahaminya sebagai satuan yang menyimpang dari nilai purata. Untuk sebaran normal, kira-kira 68% daripada 100 kumpulan batu kerikil yang kita ambil akan berada dalam julat satu standard deviation antara nilai purata dan dua sisi, dan julat dua standard deviation boleh merangkumi kira-kira 95% daripada nilai pemerhatian.

Sebagai seorang penganut agama yang taat, Dunmore menganggap kurva jam sebagai hasil ciptaan Tuhan. Menurutnya, dengan pengukuran seperti itu kita dapat mengatasi ketidakpastian dan seterusnya menakluk semua risiko, kerana pada kurva telah menggambarkan semua fenomena yang mungkin berlaku dan kebarangkalian mereka, mungkin disebabkan oleh kebetulan yang akan menghasilkan apa yang disebut penyimpangan, tetapi dengan berlalunya masa, penyimpangan ini tidak lagi mempengaruhi hukum yang kita simpulkan.

Menggunakan cara yang kita semua suka dan senang menerangkan kata-kata Tom Morver, ialah Tom kecewa adalah nombor telefon yang kadang-kadang tidak dapat dihubungi, cuba beberapa kali, dan selalu menjawab Tom Morver. Sekolah menengah juga mempunyai subjek klasik ((Oh, mengapa saya selalu menggunakan subjek sekolah menengah) adalah mengenai kadar kelulusan produk. Jika untuk sekumpulan produk, standard industri menganggap bahawa kadar sisa tidak melebihi 0.1% adalah memenuhi syarat, ini bermakna kita mengambil 10000 dari produk secara rawak, dan jika tidak melebihi 10 daripadanya, ia akan memenuhi syarat.

Tetapi kebanyakan masa, soalan ini tidak masuk akal bagi kita. Kerana kita mungkin tidak tahu berapa kadar sisa rata-rata produk, berapa besar kemungkinan satu kumpulan produk kita akan lulus ujian jika kadar sisa rata-rata lebih tinggi daripada piawaian ujian? Jika anda mengambil 20,000 produk untuk ujian, adakah 10,000 produk dapat diambil dan digunakan secara langsung?

Dipetik dari China Quantitative Investment Association