Pemikiran tentang strategi perdagangan frekuensi tinggi (2)
 1
1
 3416
3416
Artikel ini terutamanya membincangkan strategi perdagangan frekuensi tinggi, memfokuskan pada pemodelan volum terkumpul dan kejutan harga. Kertas kerja ini mencadangkan model peletakan pesanan optimum awal dengan menganalisis kesan transaksi tunggal, kejutan harga selang tetap dan volum transaksi ke atas harga. Model ini cuba mencari kedudukan dagangan yang optimum berdasarkan pemahaman volum dan kejutan harga. Andaian model dibincangkan secara mendalam, dan penilaian awal penempatan pesanan optimum dibuat dengan membandingkan pulangan yang dijangkakan sebenar dan model yang diramalkan.
Pemodelan Isipadu Terkumpul
Artikel sebelumnya memperoleh ungkapan kebarangkalian untuk volum transaksi tunggal yang lebih besar daripada nilai tertentu:
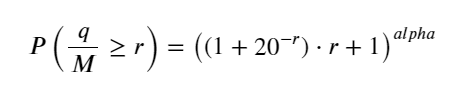
Kami juga bimbang tentang pengagihan volum dagangan dalam satu tempoh masa, yang secara intuitif harus dikaitkan dengan volum setiap transaksi dan kekerapan pesanan. Seterusnya, data diproses pada selang masa tetap. Plot pengedarannya seperti di atas.
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('HOOKUSDT-aggTrades-2023-01-27.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
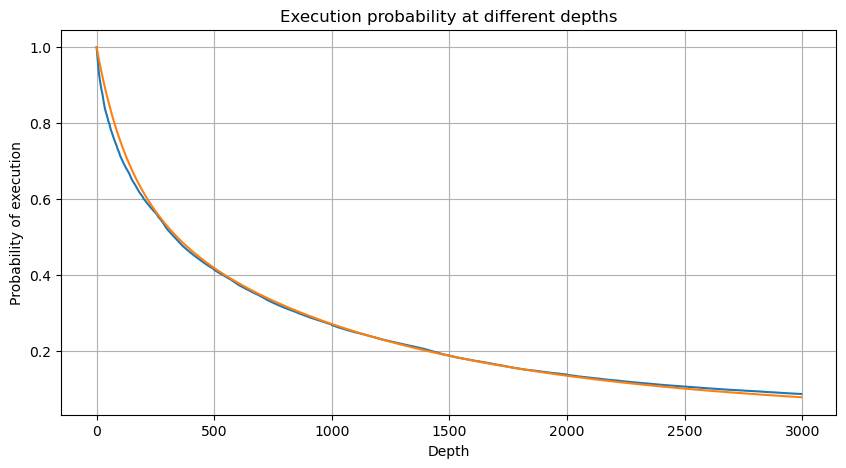
Gabungkan volum urus niaga setiap 1s, keluarkan bahagian yang tiada transaksi berlaku, dan gunakan pengedaran transaksi tunggal di atas untuk dipadankan. Ia dapat dilihat bahawa hasilnya lebih baik Jika semua urus niaga dalam 1s dianggap sebagai transaksi tunggal, masalah ini menjadi Ia telah menjadi masalah yang diselesaikan. Walau bagaimanapun, apabila kitaran dipanjangkan (berbanding dengan kekerapan transaksi), ralat didapati meningkat, dan penyelidikan mendapati bahawa ralat ini disebabkan oleh istilah pembetulan taburan Pareto sebelumnya. Ini bermakna bahawa apabila kitaran memanjang dan merangkumi lebih banyak transaksi individu, gabungan berbilang transaksi menghampiri pengedaran Pareto Dalam kes ini, istilah pembetulan harus dialih keluar.
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
buy_trades
| agg_trade_id | price | quantity | first_trade_id | last_trade_id | is_buyer_maker | date | transact_time | interval | diff | |
|---|---|---|---|---|---|---|---|---|---|---|
| 2023-01-27 00:00:00.161 | 1138369 | 2.901 | 54.3 | 3806199 | 3806201 | False | 2023-01-27 00:00:00.161 | 1674777600161 | NaN | 0.001 |
| 2023-01-27 00:00:04.140 | 1138370 | 2.901 | 291.3 | 3806202 | 3806203 | False | 2023-01-27 00:00:04.140 | 1674777604140 | 3979.0 | 0.000 |
| 2023-01-27 00:00:04.339 | 1138373 | 2.902 | 55.1 | 3806205 | 3806207 | False | 2023-01-27 00:00:04.339 | 1674777604339 | 199.0 | 0.001 |
| 2023-01-27 00:00:04.772 | 1138374 | 2.902 | 1032.7 | 3806208 | 3806223 | False | 2023-01-27 00:00:04.772 | 1674777604772 | 433.0 | 0.000 |
| 2023-01-27 00:00:05.562 | 1138375 | 2.901 | 3.5 | 3806224 | 3806224 | False | 2023-01-27 00:00:05.562 | 1674777605562 | 790.0 | 0.000 |
| … | … | … | … | … | … | … | … | … | … | … |
| 2023-01-27 23:59:57.739 | 1544370 | 3.572 | 394.8 | 5074645 | 5074651 | False | 2023-01-27 23:59:57.739 | 1674863997739 | 1224.0 | 0.002 |
| 2023-01-27 23:59:57.902 | 1544372 | 3.573 | 177.6 | 5074652 | 5074655 | False | 2023-01-27 23:59:57.902 | 1674863997902 | 163.0 | 0.001 |
| 2023-01-27 23:59:58.107 | 1544373 | 3.573 | 139.8 | 5074656 | 5074656 | False | 2023-01-27 23:59:58.107 | 1674863998107 | 205.0 | 0.000 |
| 2023-01-27 23:59:58.302 | 1544374 | 3.573 | 60.5 | 5074657 | 5074657 | False | 2023-01-27 23:59:58.302 | 1674863998302 | 195.0 | 0.000 |
| 2023-01-27 23:59:59.894 | 1544376 | 3.571 | 12.1 | 5074662 | 5074664 | False | 2023-01-27 23:59:59.894 | 1674863999894 | 1592.0 | 0.000 |
#1s内的累计分布
depths = np.array(range(0, 3000, 5))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
df_resampled = buy_trades['quantity'].resample('30S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 12000, 20))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2)
probabilities_s_2 = np.array([(depth/mean+1)**alpha for depth in depths]) # 无修正
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities,label='Probabilities (True)')
plt.plot(depths, probabilities_s, label='Probabilities (Simulation 1)')
plt.plot(depths, probabilities_s_2, label='Probabilities (Simulation 2)')
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.legend()
plt.grid(True)
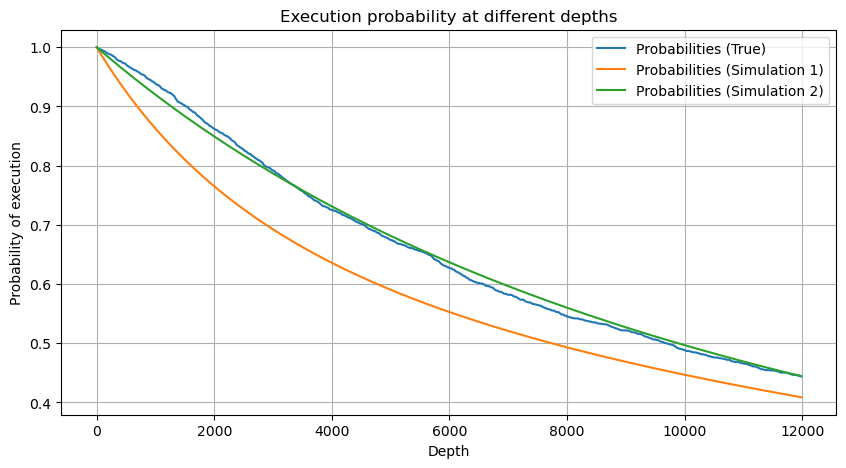
Kini kami telah meringkaskan formula umum untuk pengagihan volum dagangan terkumpul pada masa yang berbeza, dan menggunakan pengagihan transaksi tunggal untuk menyesuaikannya, tanpa perlu mengiranya secara berasingan setiap kali. Di sini kami meninggalkan proses dan memberikan formula secara langsung:
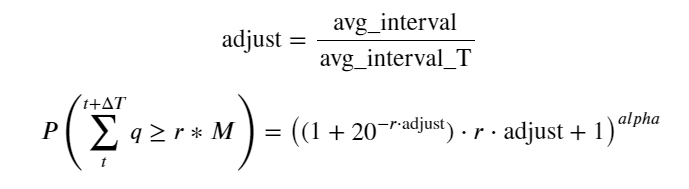
Antaranya, avg_interval mewakili selang purata antara transaksi tunggal, dan avg_interval_T mewakili selang purata selang yang perlu dianggarkan. Jika kita ingin menganggarkan masa transaksi selama 1 saat, kita perlu mengira selang purata antara peristiwa yang mengandungi transaksi dalam masa 1 saat. Jika kebarangkalian pesanan tiba mematuhi taburan Poisson, anda boleh menganggarkannya terus di sini, tetapi sisihan sebenar adalah besar, jadi saya tidak akan menerangkannya di sini.
Ambil perhatian bahawa kebarangkalian volum lebih besar daripada nilai tertentu dalam selang waktu tertentu sepatutnya agak berbeza daripada kebarangkalian sebenar urus niaga pada kedudukan itu dalam kedalaman, kerana semakin lama masa menunggu, semakin besar kemungkinan buku pesanan berubah, dan transaksi juga membawa kepada Kedalaman berubah, jadi kebarangkalian transaksi pada kedudukan kedalaman yang sama berubah dalam masa nyata apabila data dikemas kini.
df_resampled = buy_trades['quantity'].resample('2S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 6500, 10))
probabilities = np.array([np.mean(df_resampled['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
adjust = buy_trades['interval'].mean() / 2620
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/0.7178397931503168
probabilities_s = np.array([((1+20**(-depth*adjust/mean))*depth*adjust/mean+1)**(alpha) for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
Kesan harga transaksi tunggal
Data transaksi adalah harta karun, dan masih banyak data yang perlu dilombong. Kita harus memberi perhatian yang teliti terhadap kesan pesanan pada harga, yang mempengaruhi penempatan pesanan belum selesai dalam strategi. Begitu juga, berdasarkan data agregat masa_transaksi, hitung perbezaan antara harga terakhir dan harga pertama Jika terdapat hanya satu pesanan, perbezaannya ialah 0. Perkara yang aneh ialah masih terdapat sebilangan kecil hasil data dengan keputusan negatif Ini sepatutnya menjadi masalah dengan susunan data, jadi saya tidak akan membahasnya di sini.
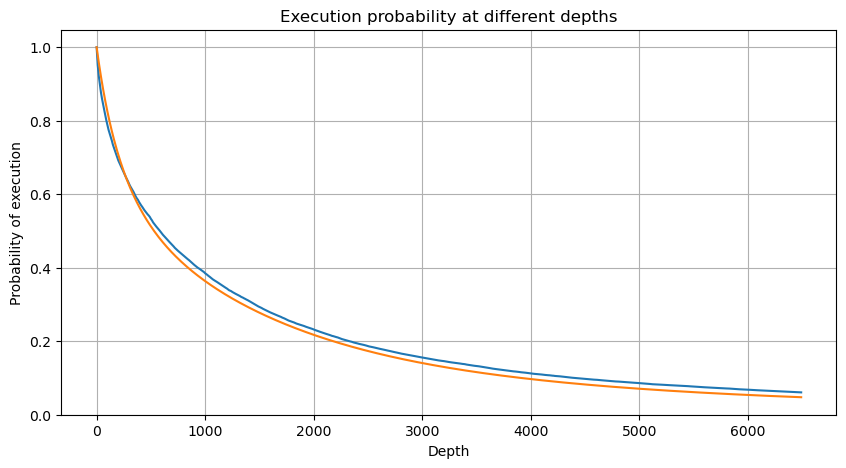
Keputusan menunjukkan bahawa perkadaran tiada impak adalah setinggi 77%, perkadaran 1 kutu ialah 16.5%, 2 kutu ialah 3.7%, 3 kutu ialah 1.2%, dan perkadaran lebih daripada 4 kutu adalah kurang daripada 1% . Ini pada asasnya mematuhi ciri-ciri fungsi eksponen, tetapi pemasangannya tidak tepat.
Jumlah urus niaga yang menyebabkan perbezaan harga yang sepadan telah dikira, dan herotan yang disebabkan oleh kesan yang terlalu besar telah dialih keluar pada asasnya mematuhi perhubungan linear, dan kira-kira setiap 1,000 volum menyebabkan turun naik harga sebanyak 1 tanda. Ia juga boleh difahami bahawa purata bilangan pesanan belum selesai berhampiran setiap harga adalah kira-kira 1,000.
diff_df = trades[trades['is_buyer_maker']==False].groupby('transact_time')['price'].agg(lambda x: abs(round(x.iloc[-1] - x.iloc[0],3)) if len(x) > 1 else 0)
buy_trades['diff'] = buy_trades['transact_time'].map(diff_df)
diff_counts = buy_trades['diff'].value_counts()
diff_counts[diff_counts>10]/diff_counts.sum()
0.000 0.769965
0.001 0.165527
0.002 0.037826
0.003 0.012546
0.004 0.005986
0.005 0.003173
0.006 0.001964
0.007 0.001036
0.008 0.000795
0.009 0.000474
0.010 0.000227
0.011 0.000187
0.012 0.000087
0.013 0.000080
Name: diff, dtype: float64
diff_group = buy_trades.groupby('diff').agg({
'quantity': 'mean',
'diff': 'last',
})
diff_group['quantity'][diff_group['diff']>0][diff_group['diff']<0.01].plot(figsize=(10,5),grid=True);
Kejutan harga pada selang masa yang tetap
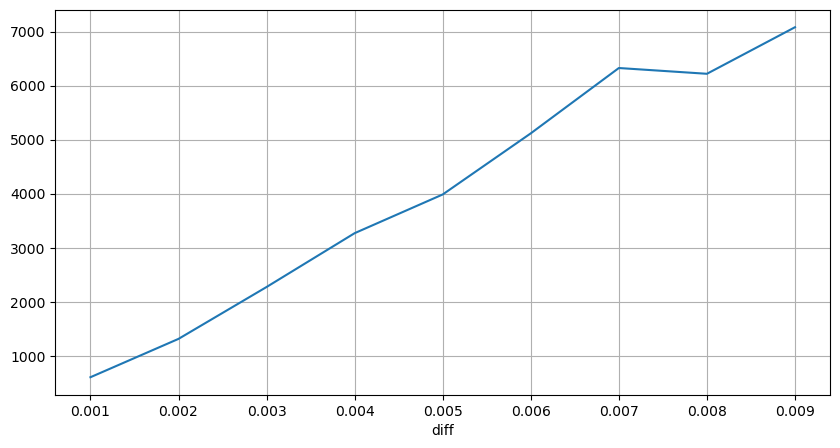
Kira kesan harga dalam masa 2 saat Perbezaan di sini ialah akan ada nilai negatif Sudah tentu, kerana hanya pesanan beli dikira di sini, kedudukan simetri akan menjadi satu tanda lebih besar. Teruskan memerhatikan hubungan antara volum dagangan dan impak, dan hanya mengira keputusan yang lebih besar daripada 0. Kesimpulannya adalah serupa dengan pesanan tunggal, yang juga merupakan perhubungan linear anggaran Setiap tanda memerlukan kira-kira 2000 volum.
df_resampled = buy_trades.resample('2S').agg({
'price': ['first', 'last', 'count'],
'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
'price_diff': df_resampled['price_diff'],
'quantity_sum': df_resampled[('quantity', 'sum')],
'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]
result_df['price_diff'][abs(result_df['price_diff'])<0.016].value_counts().sort_index().plot.bar(figsize=(10,5));
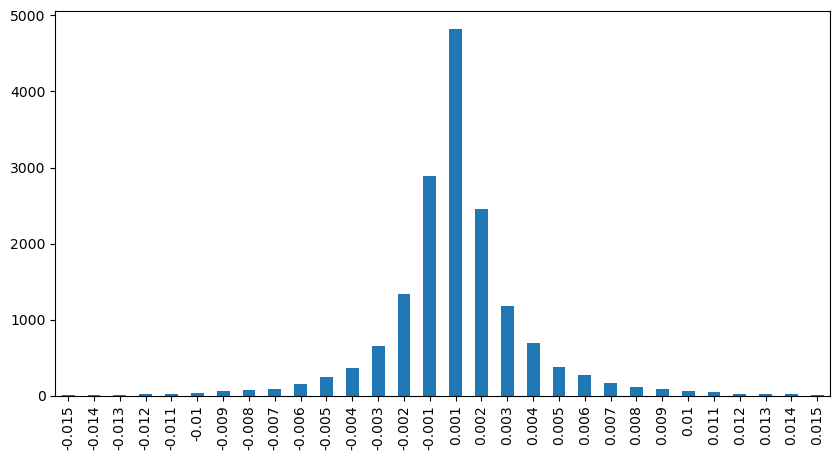
result_df['price_diff'].value_counts()[result_df['price_diff'].value_counts()>30]
0.001 7176
-0.001 3665
0.002 3069
-0.002 1536
0.003 1260
0.004 692
-0.003 608
0.005 391
-0.004 322
0.006 259
-0.005 192
0.007 146
-0.006 112
0.008 82
0.009 75
-0.007 75
-0.008 65
0.010 51
0.011 41
-0.010 31
Name: price_diff, dtype: int64
diff_group = result_df.groupby('price_diff').agg({ 'quantity_sum': 'mean'})
diff_group[(diff_group.index>0) & (diff_group.index<0.015)].plot(figsize=(10,5),grid=True);
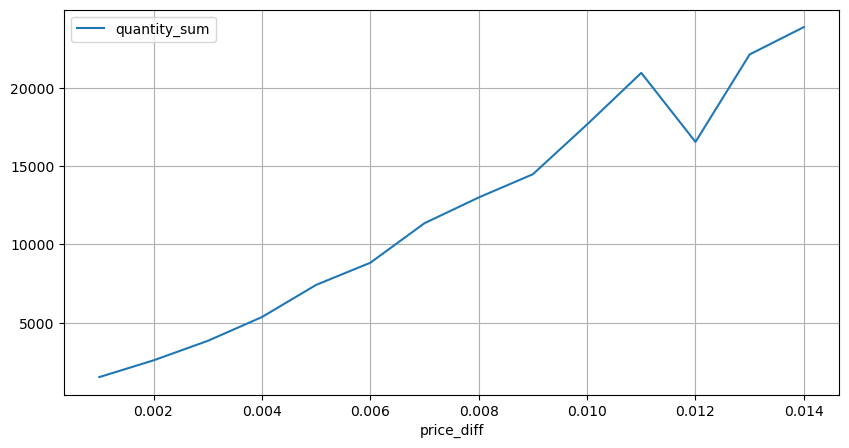
Kesan Harga Volume
Jumlah yang diperlukan untuk perubahan tanda telah dikira lebih awal, tetapi ia tidak tepat kerana ia berdasarkan andaian bahawa impak telah berlaku. Sekarang mari kita lihat impak harga yang disebabkan oleh volum dagangan.
Data di sini diambil sampel pada 1 saat, dengan 100 kuantiti sebagai 1 langkah, dan perubahan harga dalam julat kuantiti ini dikira. Beberapa kesimpulan berharga telah dibuat:
- Apabila volum belian di bawah 500, jangkaan perubahan harga akan turun, yang dijangkakan memandangkan terdapat juga pesanan jualan yang mempengaruhi harga.
- Apabila volum dagangan rendah, ia mengikut hubungan linear, iaitu lebih besar volum dagangan, lebih besar kenaikan harga.
- Lebih besar volum pesanan beli, lebih besar perubahan harga, yang selalunya mewakili penembusan harga Selepas kejayaan, harga mungkin kembali ditambah dengan pensampelan pada selang masa tetap, data tidak stabil.
- Perhatian harus diberikan kepada bahagian atas plot taburan, iaitu bahagian di mana volum sepadan dengan kenaikan harga.
- Untuk pasangan dagangan ini sahaja, versi kasar perhubungan antara volum dan perubahan harga diberikan:
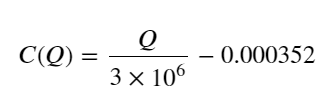
Antaranya, “C” mewakili perubahan harga dan “Q” mewakili volum pesanan belian.
df_resampled = buy_trades.resample('1S').agg({
'price': ['first', 'last', 'count'],
'quantity': 'sum'
})
df_resampled['price_diff'] = round(df_resampled[('price', 'last')] - df_resampled[('price', 'first')],3)
df_resampled['price_diff'] = df_resampled['price_diff'].fillna(0)
result_df_raw = pd.DataFrame({
'price_diff': df_resampled['price_diff'],
'quantity_sum': df_resampled[('quantity', 'sum')],
'data_count': df_resampled[('price', 'count')]
})
result_df = result_df_raw[result_df_raw['price_diff'] != 0]
df = result_df.copy()
bins = np.arange(0, 30000, 100) #
labels = [f'{i}-{i+100-1}' for i in bins[:-1]]
df.loc[:, 'quantity_group'] = pd.cut(df['quantity_sum'], bins=bins, labels=labels)
grouped = df.groupby('quantity_group')['price_diff'].mean()
grouped_df = pd.DataFrame(grouped).reset_index()
grouped_df['quantity_group_center'] = grouped_df['quantity_group'].apply(lambda x: (float(x.split('-')[0]) + float(x.split('-')[1])) / 2)
plt.figure(figsize=(10,5))
plt.scatter(grouped_df['quantity_group_center'], grouped_df['price_diff'],s=10)
plt.plot(grouped_df['quantity_group_center'], np.array(grouped_df['quantity_group_center'].values)/2e6-0.000352,color='red')
plt.xlabel('quantity_group_center')
plt.ylabel('average price_diff')
plt.title('Scatter plot of average price_diff by quantity_group')
plt.grid(True)
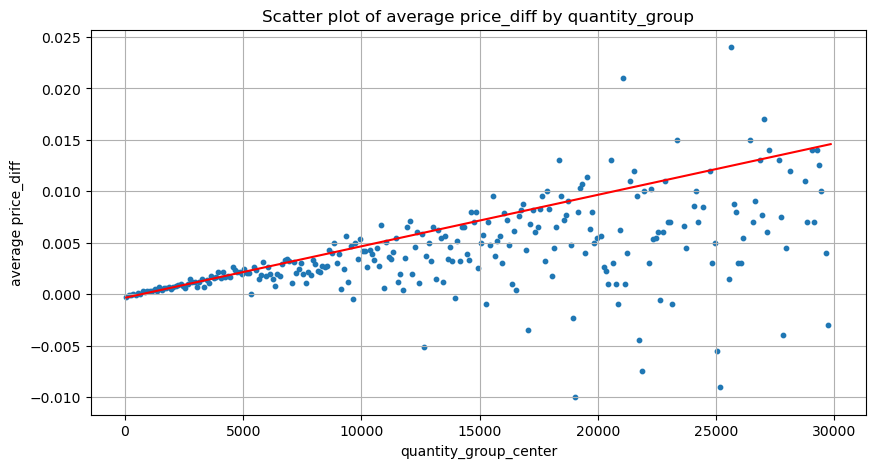
grouped_df.head(10)
| quantity_group | price_diff | quantity_group_center | |
|---|---|---|---|
| 0 | 0-199 | -0.000302 | 99.5 |
| 1 | 100-299 | -0.000124 | 199.5 |
| 2 | 200-399 | -0.000068 | 299.5 |
| 3 | 300-499 | -0.000017 | 399.5 |
| 4 | 400-599 | -0.000048 | 499.5 |
| 5 | 500-699 | 0.000098 | 599.5 |
| 6 | 600-799 | 0.000006 | 699.5 |
| 7 | 700-899 | 0.000261 | 799.5 |
| 8 | 800-999 | 0.000186 | 899.5 |
| 9 | 900-1099 | 0.000299 | 999.5 |
Kedudukan pesanan optimum awal
Dengan pemodelan volum dagangan dan model kasar volum dagangan sepadan dengan kesan harga, nampaknya kedudukan pesanan optimum boleh dikira. Mari kita buat beberapa andaian dan berikan kedudukan harga optimum yang tidak bertanggungjawab.
- Andaikan bahawa harga kembali kepada nilai asalnya selepas kejutan (ini sudah tentu tidak mungkin dan memerlukan analisis semula perubahan harga selepas kejutan)
- Andaikan bahawa pengagihan volum dagangan dan kekerapan pesanan dalam tempoh ini memenuhi keperluan pratetap (ini juga tidak tepat, kerana nilai satu hari digunakan untuk anggaran, dan transaksi mempunyai pengelompokan yang jelas).
- Andaikan hanya satu pesanan jual berlaku semasa masa simulasi dan kemudian kedudukan ditutup.
- Dengan mengandaikan bahawa selepas pesanan dilaksanakan, terdapat pesanan belian lain untuk terus menaikkan harga, terutamanya apabila volum sangat rendah Kesan ini diabaikan di sini dan hanya diandaikan bahawa ia akan kembali.
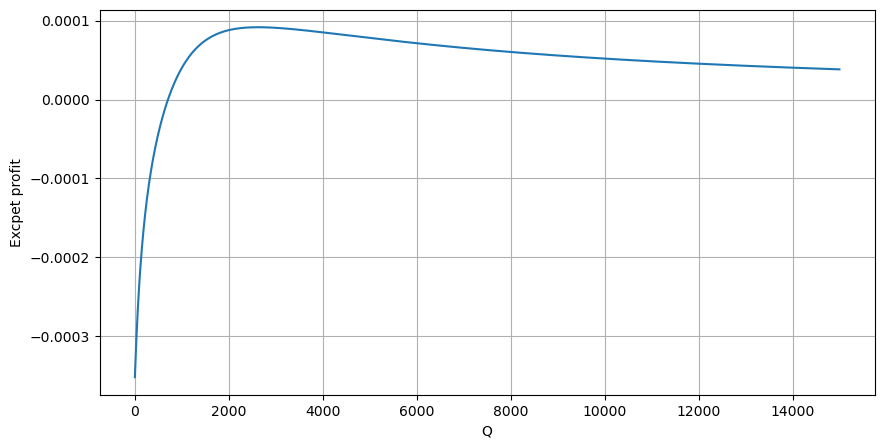
Mula-mula, tulis pulangan yang dijangkakan yang mudah, iaitu, kebarangkalian pesanan belian terkumpul lebih besar daripada Q dalam masa 1 saat, didarab dengan kadar pulangan yang dijangka (iaitu, harga impak):
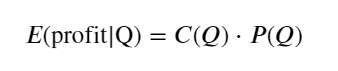
Menurut graf, pulangan yang dijangkakan adalah maksimum pada sekitar 2500, iaitu kira-kira 2.5 kali ganda volum dagangan purata. Maksudnya, pesanan jual hendaklah diletakkan pada 2500. Perlu ditekankan sekali lagi bahawa paksi mendatar mewakili volum dagangan dalam masa 1 saat dan tidak boleh disamakan dengan kedudukan kedalaman. Dan ini adalah pada masa apabila masih terdapat kekurangan data mendalam yang sangat penting, dan ia hanya berdasarkan spekulasi berdasarkan dagangan.
ringkaskan
Didapati bahawa pengagihan volum pada selang masa yang berbeza adalah penskalaan mudah bagi pengagihan volum bagi satu transaksi. Kami juga membuat model pulangan yang mudah berdasarkan kejutan harga dan kebarangkalian transaksi Hasil model ini adalah selaras dengan jangkaan kami Jika jumlah pesanan jual adalah kecil, ia menunjukkan jumlah volum tertentu mempunyai margin keuntungan, dan lebih besar volum urus niaga, lebih tinggi margin keuntungan Lebih besar kebarangkalian, lebih rendah terdapat saiz yang optimum di tengah, yang juga kedudukan penempatan pesanan yang dicari oleh strategi. Sudah tentu, model ini masih terlalu mudah Dalam artikel seterusnya, saya akan terus membincangkannya secara mendalam.
#1s内的累计分布
df_resampled = buy_trades['quantity'].resample('1S').sum()
df_resampled = df_resampled.to_frame(name='quantity')
df_resampled = df_resampled[df_resampled['quantity']>0]
depths = np.array(range(0, 15000, 10))
mean = df_resampled['quantity'].mean()
alpha = np.log(np.mean(df_resampled['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([((1+20**(-depth/mean))*depth/mean+1)**(alpha) for depth in depths])
profit_s = np.array([depth/2e6-0.000352 for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities_s*profit_s)
plt.xlabel('Q')
plt.ylabel('Excpet profit')
plt.grid(True)