Pemikiran tentang strategi perdagangan frekuensi tinggi (3)
 0
0
 2664
2664

Dalam artikel sebelumnya, saya memperkenalkan cara untuk memodelkan volum dagangan terkumpul dan menganalisis secara ringkas fenomena kejutan harga. Artikel ini akan terus menganalisis data pesanan dagangan. Dalam dua hari yang lalu, YGG melancarkan kontrak berasaskan U Binance, dan harganya sangat turun naik, malah volum dagangan melebihi BTC pada satu ketika. Mari kita analisa hari ini.
Selang masa pesanan
Secara umum, diandaikan bahawa masa pesanan tiba mengikuti proses Poisson Berikut adalah artikel yang memperkenalkanProses Poisson . Saya akan menunjukkan ini di bawah.
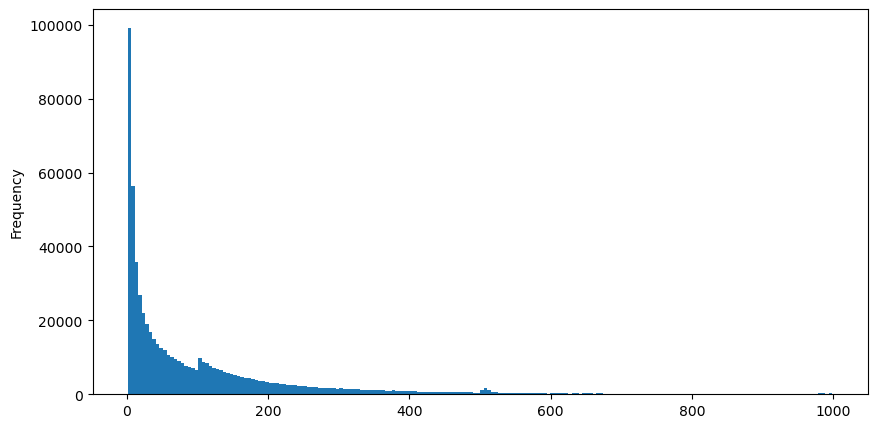
Muat turun aggTrades pada 5 Ogos, terdapat 1,931,193 dagangan secara keseluruhan, yang agak keterlaluan. Pertama, mari kita lihat pengedaran pesanan belian Kita dapat melihat bahawa terdapat puncak tempatan yang tidak sekata pada sekitar 100ms dan 500ms Ini sepatutnya disebabkan oleh pesanan berjadual yang diamanahkan oleh Iceberg sebab-sebab mengapa keadaan pasaran pada hari itu adalah luar biasa.
Fungsi jisim kebarangkalian (PMF) taburan Poisson diberikan oleh:
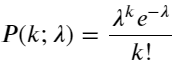
dalam:
- k ialah bilangan acara yang kita minati.
- λ ialah purata kadar kejadian bagi setiap unit masa (atau unit ruang).
- P(k; λ) ialah kebarangkalian tepat k peristiwa berlaku, diberi purata kadar kejadian λ.
Dalam proses Poisson, selang masa antara peristiwa mengikuti taburan eksponen. Fungsi ketumpatan kebarangkalian (PDF) bagi taburan eksponen diberikan oleh:
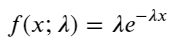
Melalui pemasangan, didapati keputusan agak berbeza daripada hasil jangkaan taburan Poisson Proses Poisson meremehkan kekerapan selang yang panjang dan melebihkan kekerapan selang yang pendek. (Taburan selang masa sebenar lebih hampir kepada taburan Pareto yang diubah suai)
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('YGGUSDT-aggTrades-2023-08-05.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
buy_trades['interval'][buy_trades['interval']<1000].plot.hist(bins=200,figsize=(10, 5));
Intervals = np.array(range(0, 1000, 5))
mean_intervals = buy_trades['interval'].mean()
buy_rates = 1000/mean_intervals
probabilities = np.array([np.mean(buy_trades['interval'] > interval) for interval in Intervals])
probabilities_s = np.array([np.e**(-buy_rates*interval/1000) for interval in Intervals])
plt.figure(figsize=(10, 5))
plt.plot(Intervals, probabilities)
plt.plot(Intervals, probabilities_s)
plt.xlabel('Intervals')
plt.ylabel('Probability')
plt.grid(True)
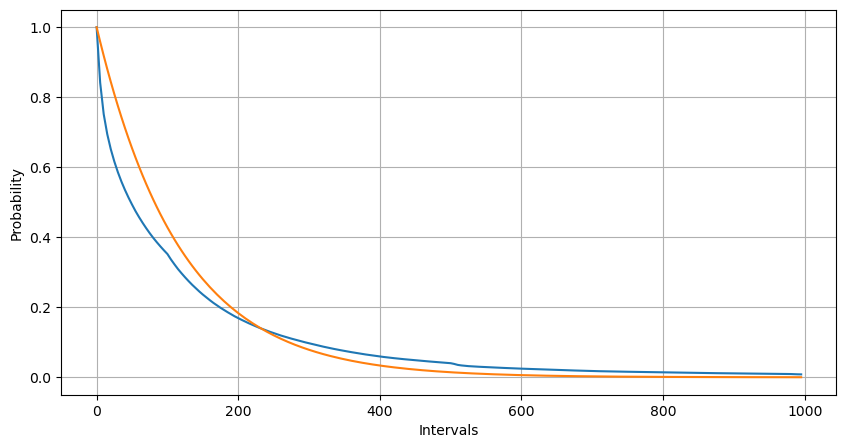
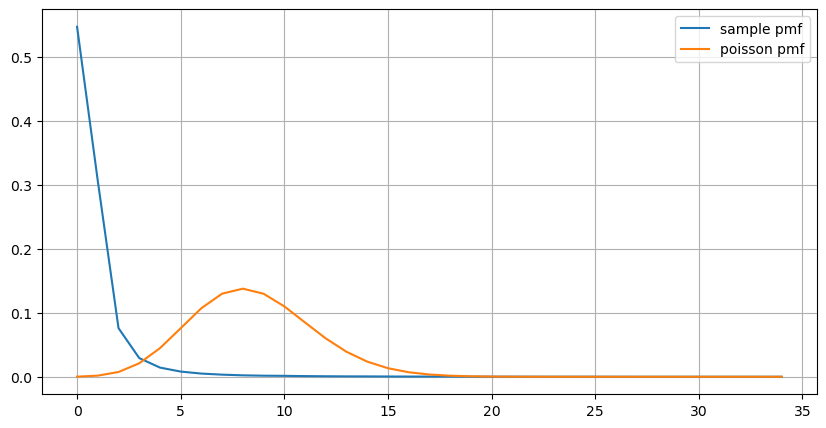
Taburan statistik bilangan pesanan yang berlaku dalam masa 1 saat dan perbandingan dengan taburan Poisson juga menunjukkan perbezaan yang sangat jelas. Taburan Poisson amat meremehkan kekerapan kejadian berkemungkinan rendah. Penyebab yang mungkin:
- Kadar kejadian tidak tetap: Proses Poisson mengandaikan bahawa kadar purata kejadian yang berlaku dalam mana-mana tempoh masa tertentu adalah malar. Jika andaian ini tidak berlaku, maka taburan data akan menyimpang daripada taburan Poisson.
- Interaksi proses: Satu lagi andaian asas proses Poisson ialah peristiwa adalah bebas antara satu sama lain. Jika peristiwa dunia nyata mempengaruhi satu sama lain, pengedarannya mungkin menyimpang daripada pengedaran Poisson.
Maksudnya, dalam persekitaran sebenar, kekerapan pesanan adalah tidak tetap, perlu dikemas kini dalam masa nyata, dan insentif akan berlaku, iaitu, lebih banyak pesanan dalam masa tetap akan merangsang lebih banyak pesanan. Ini menjadikannya mustahil untuk menetapkan satu parameter dalam strategi.
result_df = buy_trades.resample('0.1S').agg({
'price': 'count',
'quantity': 'sum'
}).rename(columns={'price': 'order_count', 'quantity': 'quantity_sum'})
count_df = result_df['order_count'].value_counts().sort_index()[result_df['order_count'].value_counts()>20]
(count_df/count_df.sum()).plot(figsize=(10,5),grid=True,label='sample pmf');
from scipy.stats import poisson
prob_values = poisson.pmf(count_df.index, 1000/mean_intervals)
plt.plot(count_df.index, prob_values,label='poisson pmf');
plt.legend() ;
Parameter kemas kini masa nyata
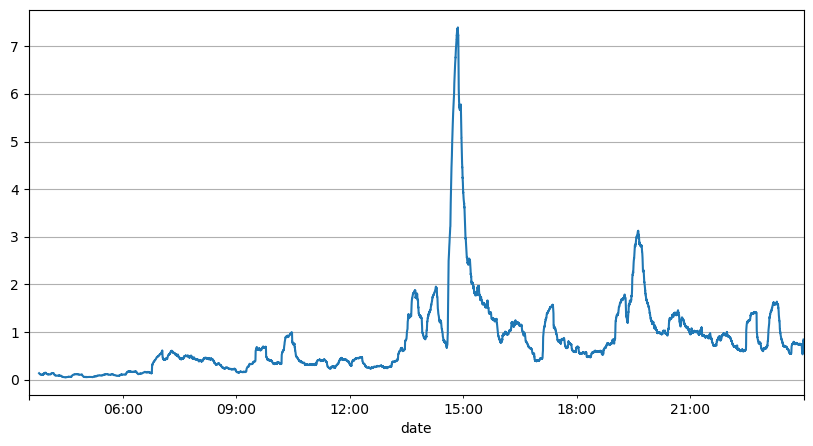
Analisis selang pesanan sebelum ini menunjukkan bahawa parameter tetap tidak sesuai untuk keadaan pasaran sebenar, dan parameter utama penerangan pasaran strategi perlu dikemas kini dalam masa nyata. Penyelesaian paling mudah untuk difikirkan ialah purata bergerak bagi tetingkap gelongsor. Dua angka di bawah adalah kekerapan pesanan belian dalam masa 1 saat dan purata 1000 tetingkap volum dagangan Dapat dilihat bahawa terdapat fenomena pengelompokan dalam urus niaga, iaitu kekerapan pesanan adalah lebih tinggi daripada biasa bagi sesuatu. tempoh masa, dan kelantangan pada masa ini juga meningkat secara serentak. Di sini, min sebelumnya digunakan untuk meramalkan nilai detik terkini, dan min ralat mutlak baki digunakan untuk mengukur kualiti ramalan.
Daripada graf, kita juga boleh memahami mengapa kekerapan pesanan jauh menyimpang daripada taburan Poisson Walaupun purata bilangan pesanan sesaat hanya 8.5 kali, dalam kes yang melampau, purata bilangan pesanan sesaat menyimpang jauh daripadanya.
Didapati di sini bahawa menggunakan min dua saat sebelumnya untuk meramal ralat baki adalah yang paling kecil dan jauh lebih baik daripada hasil ramalan min mudah.
result_df['order_count'][::10].rolling(1000).mean().plot(figsize=(10,5),grid=True);
result_df
| order_count | quantity_sum | |
|---|---|---|
| 2023-08-05 03:30:06.100 | 1 | 76.0 |
| 2023-08-05 03:30:06.200 | 0 | 0.0 |
| 2023-08-05 03:30:06.300 | 0 | 0.0 |
| 2023-08-05 03:30:06.400 | 1 | 416.0 |
| 2023-08-05 03:30:06.500 | 0 | 0.0 |
| … | … | … |
| 2023-08-05 23:59:59.500 | 3 | 9238.0 |
| 2023-08-05 23:59:59.600 | 0 | 0.0 |
| 2023-08-05 23:59:59.700 | 1 | 3981.0 |
| 2023-08-05 23:59:59.800 | 0 | 0.0 |
| 2023-08-05 23:59:59.900 | 2 | 534.0 |
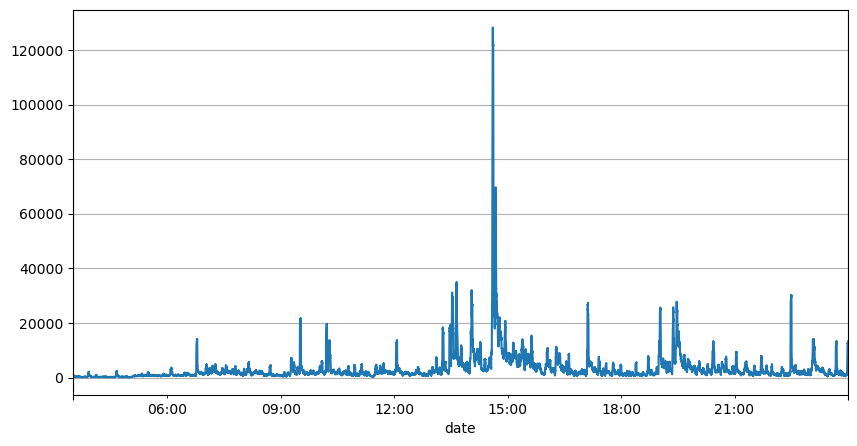
result_df['quantity_sum'].rolling(1000).mean().plot(figsize=(10,5),grid=True);
(result_df['order_count'] - result_df['mean_count'].mean()).abs().mean()
6.985628185332997
result_df['mean_count'] = result_df['order_count'].ewm(alpha=0.11, adjust=False).mean()
(result_df['order_count'] - result_df['mean_count'].shift()).abs().mean()
0.6727616961866929
result_df['mean_quantity'] = result_df['quantity_sum'].ewm(alpha=0.1, adjust=False).mean()
(result_df['quantity_sum'] - result_df['mean_quantity'].shift()).abs().mean()
4180.171479076811
ringkaskan
Artikel ini memperkenalkan secara ringkas sebab selang masa pesanan menyimpang daripada proses Poisson, terutamanya kerana parameter berubah mengikut masa. Untuk meramalkan pasaran dengan lebih tepat, strategi perlu membuat ramalan masa nyata pada parameter asas pasaran. Sisa boleh digunakan untuk mengukur kualiti ramalan Contoh di atas adalah yang paling mudah Terdapat banyak kajian berkaitan analisis siri masa, pengagregatan turun naik, dan lain-lain, yang boleh dipertingkatkan lagi.