Dalam artikel ini, kami akan menulis strategi perdagangan hari. Ia akan menggunakan konsep perdagangan klasik “pasangan dagangan pengembalian min”. Dalam contoh ini, kami akan menggunakan dua dana dagangan bursa (ETF), SPY dan IWM, yang berdagang di Bursa Saham New York (NYSE) dan cuba mewakili indeks pasaran saham A.S., S&P 500 dan Russell 2000.” .

Strategi ini mencipta “carry” dengan pergi panjang satu ETF dan pendek satu lagi. Nisbah panjang-pendek boleh ditakrifkan dalam pelbagai cara, contohnya menggunakan kaedah siri masa kointegrasi statistik. Dalam senario ini, kami akan mengira nisbah lindung nilai antara SPY dan IWM melalui regresi linear bergulir. Ini akan membolehkan kami mencipta “spread” antara SPY dan IWM yang dinormalkan kepada skor z. Apabila skor z melebihi ambang tertentu, isyarat dagangan dijana kerana kami percaya bahawa “sebaran” ini akan kembali kepada min.

Rasional bagi strategi tersebut ialah kedua-dua SPY dan IWM mewakili kira-kira senario pasaran yang sama, iaitu prestasi harga saham sekumpulan syarikat A.S. besar dan kecil. Premisnya ialah jika anda menerima teori harga “penulangan min”, maka ia akan sentiasa berbalik, kerana “peristiwa” boleh menjejaskan S&P500 dan Russell 2000 secara berasingan dalam tempoh masa yang sangat singkat, tetapi “perbezaan kadar faedah” antara mereka akan sentiasa akan kembali kepada min biasa, dan siri harga jangka panjang kedua-duanya sentiasa disatukan.

Strategi

Strategi dilaksanakan seperti berikut:

Data - Dapatkan carta lilin SPY dan IWM 1 minit dari April 2007 hingga Februari 2014.

Pemprosesan - Jajarkan data dengan betul dan padamkan bar yang tiada antara satu sama lain. (Jika satu pihak hilang, kedua-dua belah pihak akan dipadamkan)

Spread - Nisbah lindung nilai antara dua ETF dikira menggunakan regresi linear bergolek. Ditakrifkan sebagai pekali regresi beta menggunakan tetingkap lihat belakang yang digerakkan ke hadapan sebanyak 1 bar dan pekali regresi dikira semula. Oleh itu, nisbah lindung nilai βi, bi K-garis digunakan untuk mengesan garis-K dengan mengira titik silang dari bi-1-k kepada bi-1.

Z-Score - Nilai Spread Standard dikira dengan cara biasa. Ini bermakna menolak min taburan (sampel) dan membahagikan dengan sisihan piawai taburan (sampel). Sebab untuk melakukan ini adalah untuk menjadikan parameter ambang lebih mudah difahami kerana Z-Score ialah kuantiti tanpa dimensi. Saya sengaja memperkenalkan “kecondongan pandang ke hadapan” ke dalam pengiraan untuk menunjukkan betapa halusnya pengiraan itu. Cubalah!

Dagangan - Isyarat panjang dijana apabila nilai z-skor negatif jatuh di bawah ambang yang telah ditetapkan (atau selepas dioptimumkan), manakala isyarat pendek dijana dengan cara yang bertentangan. Apabila nilai mutlak skor z jatuh di bawah ambang tambahan, isyarat untuk menutup kedudukan dijana. Untuk strategi ini, saya (agak sewenang-wenangnya) memilih |z| = 2 sebagai ambang masuk dan |z| = 1 sebagai ambang keluar. Dengan mengandaikan pengembalian min memainkan peranan dalam penyebaran, perkara di atas diharapkan dapat menangkap hubungan arbitraj ini dan memberikan keuntungan yang lumayan.

Mungkin cara terbaik untuk memahami strategi secara mendalam adalah dengan benar-benar melaksanakannya. Bahagian berikut memperincikan kod Python lengkap (fail tunggal) yang digunakan untuk melaksanakan strategi pengembalian min ini. Saya telah menambah ulasan kod terperinci untuk membantu anda memahami dengan lebih baik.

Pelaksanaan Python

Seperti semua tutorial Python/pandas, persekitaran Python anda mesti disediakan seperti yang diterangkan dalam tutorial ini. Setelah persediaan selesai, tugas pertama ialah mengimport perpustakaan Python yang diperlukan. Ini diperlukan untuk menggunakan matplotlib dan panda.

Versi perpustakaan khusus yang saya gunakan adalah seperti berikut:

Python - 2.7.3 NumPy - 1.8.0 pandas - 0.12.0 matplotlib - 1.1.0

Mari teruskan dan import perpustakaan ini:

# mr_spy_iwm.py

import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd

Fungsi create_pairs_dataframe berikut mengimport dua fail CSV yang mengandungi candlestick intraday dua simbol. Dalam kes kami, ini adalah SPY dan IWM. Ia kemudian mencipta “sepasang bingkai data” berasingan yang menggunakan indeks kedua-dua fail asal. Cap masa mereka mungkin berbeza-beza disebabkan oleh urus niaga yang terlepas dan ralat. Ini adalah salah satu faedah utama menggunakan perpustakaan analisis data seperti panda. Kami mengendalikan kod “boilerplate” dengan cara yang sangat cekap.

# mr_spy_iwm.py
def create_pairs_dataframe(datadir, symbols):
    """Creates a pandas DataFrame containing the closing price
    of a pair of symbols based on CSV files containing a datetime
    stamp and OHLCV data."""
 
    # Open the individual CSV files and read into pandas DataFrames
    print "Importing CSV data..."
    sym1 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[0]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
    sym2 = pd.io.parsers.read_csv(os.path.join(datadir, '%s.csv' % symbols[1]),
                                  header=0, index_col=0, 
                                  names=['datetime','open','high','low','close','volume','na'])
 
    # Create a pandas DataFrame with the close prices of each symbol
    # correctly aligned and dropping missing entries
    print "Constructing dual matrix for %s and %s..." % symbols    
    pairs = pd.DataFrame(index=sym1.index)
    pairs['%s_close' % symbols[0].lower()] = sym1['close']
    pairs['%s_close' % symbols[1].lower()] = sym2['close']
    pairs = pairs.dropna()
    return pairs

Langkah seterusnya ialah melakukan regresi linear bergulir antara SPY dan IWM. Dalam senario ini, IWM ialah peramal (‘x’) dan SPY ialah respons (‘y’). Saya menetapkan tetingkap lihat balik lalai sebanyak 100 batang lilin. Seperti yang dinyatakan di atas, ini adalah parameter strategi. Agar strategi dianggap teguh, sebaiknya kami ingin melihat laporan pulangan yang cembung sepanjang tempoh lihat kembali (atau beberapa ukuran prestasi lain). Oleh itu, pada peringkat seterusnya kod, kami akan melakukan analisis sensitiviti dengan mengubah tempoh lihat kembali dalam skop.

Selepas mengira pekali beta bergolek dalam model regresi linear untuk SPY-IWM, tambahkannya pada pasangan DataFrame dan alih keluar baris kosong. Ini membina set pertama batang lilin, yang sama dengan ukuran dipangkas bagi panjang lihat ke belakang. Kami kemudian mencipta sebaran antara dua ETF, satu unit SPY dan satu unit -βi IWM. Jelas sekali, ini bukan senario yang realistik, kerana kami menggunakan sejumlah kecil IWM, yang tidak mungkin dalam pelaksanaan praktikal.

Akhir sekali, kami mencipta skor z bagi sebaran, dikira dengan menolak min sebaran dan menormalkan dengan sisihan piawai sebaran. Adalah penting untuk ambil perhatian bahawa terdapat “berat pandang ke hadapan” yang agak halus di tempat kerja di sini. Saya meninggalkannya dalam kod dengan sengaja kerana saya ingin menyerlahkan betapa mudahnya untuk membuat kesilapan seperti ini dalam penyelidikan. Kirakan min dan sisihan piawai bagi keseluruhan siri masa taburan. Jika ini bertujuan untuk menggambarkan ketepatan sejarah yang sebenar, maka maklumat ini tidak boleh diperolehi kerana ia secara tersirat menggunakan maklumat dari masa hadapan. Oleh itu, kita harus menggunakan min rolling dan stdev untuk mengira skor-z.

# mr_spy_iwm.py
 
def calculate_spread_zscore(pairs, symbols, lookback=100):
    """Creates a hedge ratio between the two symbols by calculating
    a rolling linear regression with a defined lookback period. This
    is then used to create a z-score of the 'spread' between the two
    symbols based on a linear combination of the two."""
     
    # Use the pandas Ordinary Least Squares method to fit a rolling
    # linear regression between the two closing price time series
    print "Fitting the rolling Linear Regression..."
    model = pd.ols(y=pairs['%s_close' % symbols[0].lower()], 
                   x=pairs['%s_close' % symbols[1].lower()],
                   window=lookback)
 
    # Construct the hedge ratio and eliminate the first 
    # lookback-length empty/NaN period
    pairs['hedge_ratio'] = model.beta['x']
    pairs = pairs.dropna()
 
    # Create the spread and then a z-score of the spread
    print "Creating the spread/zscore columns..."
    pairs['spread'] = pairs['spy_close'] - pairs['hedge_ratio']*pairs['iwm_close']
    pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread']))/np.std(pairs['spread'])
    return pairs

Dalam create_long_short_market_signals, cipta isyarat dagangan. Ini dikira dengan mengukur nilai skor z yang melebihi ambang. Apabila nilai mutlak skor z kurang daripada atau sama dengan ambang (lebih kecil) yang lain, isyarat untuk menutup kedudukan diberikan.

Untuk mencapai matlamat ini, adalah perlu untuk menentukan sama ada strategi perdagangan adalah “membuka” atau “menutup” untuk setiap K-line. Long_market dan short_market ialah dua pembolehubah yang ditakrifkan untuk menjejaki kedudukan panjang dan pendek. Malangnya, ia adalah perlahan dari segi pengiraan kerana ia adalah lebih mudah untuk memprogram secara berulang daripada pendekatan vektor. Walaupun carta candlestick 1 minit memerlukan ~700,000 titik data bagi setiap fail CSV, ia masih agak pantas untuk dikira pada desktop lama saya!

Untuk mengulangi panda DataFrame (operasi yang diakui tidak biasa), perlu menggunakan kaedah iterrows, yang menyediakan penjana boleh lelar:

# mr_spy_iwm.py
 
def create_long_short_market_signals(pairs, symbols, 
                                     z_entry_threshold=2.0, 
                                     z_exit_threshold=1.0):
    """Create the entry/exit signals based on the exceeding of 
    z_enter_threshold for entering a position and falling below
    z_exit_threshold for exiting a position."""
 
    # Calculate when to be long, short and when to exit
    pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
    pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
    pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0
 
    # These signals are needed because we need to propagate a
    # position forward, i.e. we need to stay long if the zscore
    # threshold is less than z_entry_threshold by still greater
    # than z_exit_threshold, and vice versa for shorts.
    pairs['long_market'] = 0.0
    pairs['short_market'] = 0.0
 
    # These variables track whether to be long or short while
    # iterating through the bars
    long_market = 0
    short_market = 0
 
    # Calculates when to actually be "in" the market, i.e. to have a
    # long or short position, as well as when not to be.
    # Since this is using iterrows to loop over a dataframe, it will
    # be significantly less efficient than a vectorised operation,
    # i.e. slow!
    print "Calculating when to be in the market (long and short)..."
    for i, b in enumerate(pairs.iterrows()):
        # Calculate longs
        if b[1]['longs'] == 1.0:
            long_market = 1            
        # Calculate shorts
        if b[1]['shorts'] == 1.0:
            short_market = 1
        # Calculate exists
        if b[1]['exits'] == 1.0:
            long_market = 0
            short_market = 0
        # This directly assigns a 1 or 0 to the long_market/short_market
        # columns, such that the strategy knows when to actually stay in!
        pairs.ix[i]['long_market'] = long_market
        pairs.ix[i]['short_market'] = short_market
    return pairs

Pada peringkat ini, kami mengemas kini pasangan untuk mengandungi isyarat panjang dan pendek sebenar, yang membolehkan kami menentukan sama ada kami perlu membuka kedudukan. Sekarang kita perlu mencipta portfolio untuk menjejaki nilai pasaran jawatan tersebut. Tugas pertama ialah mencipta lajur kedudukan yang menggabungkan isyarat panjang dan pendek. Ini akan mengandungi senarai elemen dari (1,0,-1) dengan 1 mewakili kedudukan panjang, 0 tidak mewakili kedudukan (yang sepatutnya ditutup) dan -1 mewakili kedudukan pendek. Lajur sym1 dan sym2 mewakili nilai pasaran kedudukan SPY dan IWM pada akhir setiap batang lilin.

Setelah nilai pasaran ETF dibuat, kami menjumlahkannya untuk menghasilkan jumlah nilai pasaran pada akhir setiap batang lilin. Ia kemudian ditukar kepada nilai pulangan melalui kaedah pct_change objek itu. Baris kod seterusnya membersihkan entri yang salah (NaN dan elemen inf) dan akhirnya mengira keluk ekuiti lengkap.

# mr_spy_iwm.py
 
def create_portfolio_returns(pairs, symbols):
    """Creates a portfolio pandas DataFrame which keeps track of
    the account equity and ultimately generates an equity curve.
    This can be used to generate drawdown and risk/reward ratios."""
     
    # Convenience variables for symbols
    sym1 = symbols[0].lower()
    sym2 = symbols[1].lower()
 
    # Construct the portfolio object with positions information
    # Note that minuses to keep track of shorts!
    print "Constructing a portfolio..."
    portfolio = pd.DataFrame(index=pairs.index)
    portfolio['positions'] = pairs['long_market'] - pairs['short_market']
    portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
    portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
    portfolio['total'] = portfolio[sym1] + portfolio[sym2]
 
    # Construct a percentage returns stream and eliminate all 
    # of the NaN and -inf/+inf cells
    print "Constructing the equity curve..."
    portfolio['returns'] = portfolio['total'].pct_change()
    portfolio['returns'].fillna(0.0, inplace=True)
    portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
    portfolio['returns'].replace(-1.0, 0.0, inplace=True)
 
    # Calculate the full equity curve
    portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
    return portfolio

Fungsi utama mengikat semuanya bersama-sama. Fail CSV intraday terletak di laluan datadir. Pastikan anda mengubah suai kod berikut untuk menunjuk ke direktori khusus anda.

Untuk menentukan sejauh mana sensitif strategi kepada tempoh lihat balik, adalah perlu untuk mengira julat metrik prestasi lihat balik. Saya memilih jumlah peratusan pulangan akhir portfolio sebagai metrik prestasi dan julat lihat balik.[50,200] dengan kenaikan 10. Anda boleh lihat dalam kod di bawah bahawa fungsi sebelumnya dibalut dengan gelung for pada julat ini dan ambang lain kekal sama. Tugas terakhir adalah untuk mencipta carta garisan lihat balik berbanding pulangan menggunakan matplotlib:

# mr_spy_iwm.py
 
if __name__ == "__main__":
    datadir = '/your/path/to/data/'  # Change this to reflect your data path!
    symbols = ('SPY', 'IWM')
 
    lookbacks = range(50, 210, 10)
    returns = []
 
    # Adjust lookback period from 50 to 200 in increments
    # of 10 in order to produce sensitivities
    for lb in lookbacks: 
        print "Calculating lookback=%s..." % lb
        pairs = create_pairs_dataframe(datadir, symbols)
        pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
        pairs = create_long_short_market_signals(pairs, symbols, 
                                                z_entry_threshold=2.0, 
                                                z_exit_threshold=1.0)
 
        portfolio = create_portfolio_returns(pairs, symbols)
        returns.append(portfolio.ix[-1]['returns'])
 
    print "Plot the lookback-performance scatterchart..."
    plt.plot(lookbacks, returns, '-o')
    plt.show()

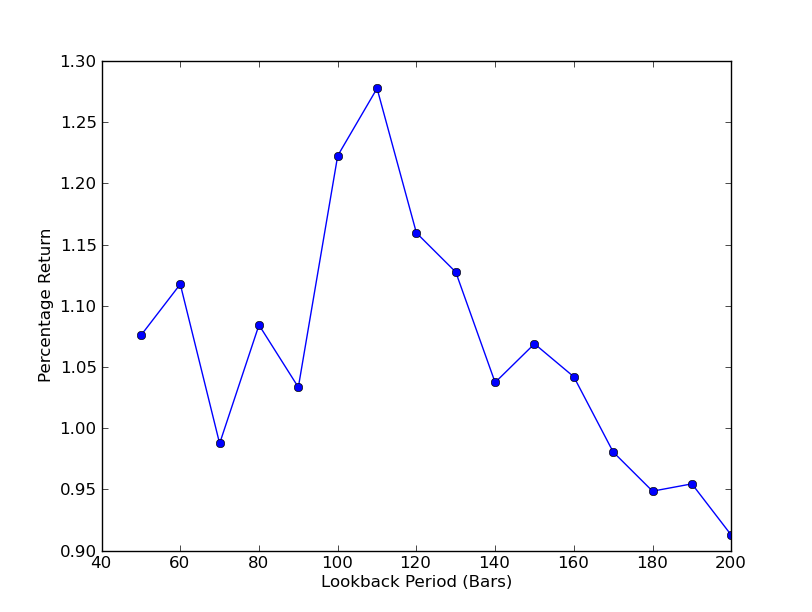
Kini anda boleh melihat graf tinjauan semula dan pulangan. Ambil perhatian bahawa terdapat maksimum “global” untuk tinjauan semula, bersamaan dengan 110 bar. Jika kita melihat situasi di mana tinjauan ke belakang tidak ada kaitan dengan pulangan, ini adalah kerana:

SPY-IWM Linear Regresi Lindung Nilai Nisbah Tinjau Balik Tempoh Analisis Sensitiviti

Tiada artikel ujian belakang akan lengkap tanpa keluk keuntungan yang mencerun ke atas! Jadi jika anda ingin merancang pulangan keuntungan terkumpul berbanding masa, anda boleh menggunakan kod berikut. Ia akan memplot portfolio akhir yang dijana daripada kajian parameter lihat balik. Oleh itu, adalah perlu untuk memilih lihat balik mengikut carta yang ingin anda gambarkan. Carta ini juga memplot pulangan SPY dalam tempoh yang sama untuk membantu perbandingan:

# mr_spy_iwm.py
 
    # This is still within the main function
    print "Plotting the performance charts..."
    fig = plt.figure()
    fig.patch.set_facecolor('white')
 
    ax1 = fig.add_subplot(211,  ylabel='%s growth (%%)' % symbols[0])
    (pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)
 
    ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
    portfolio['returns'].plot(ax=ax2, lw=2.)
 
    fig.show()

Tempoh lihat balik untuk carta lengkung ekuiti berikut ialah 100 hari:

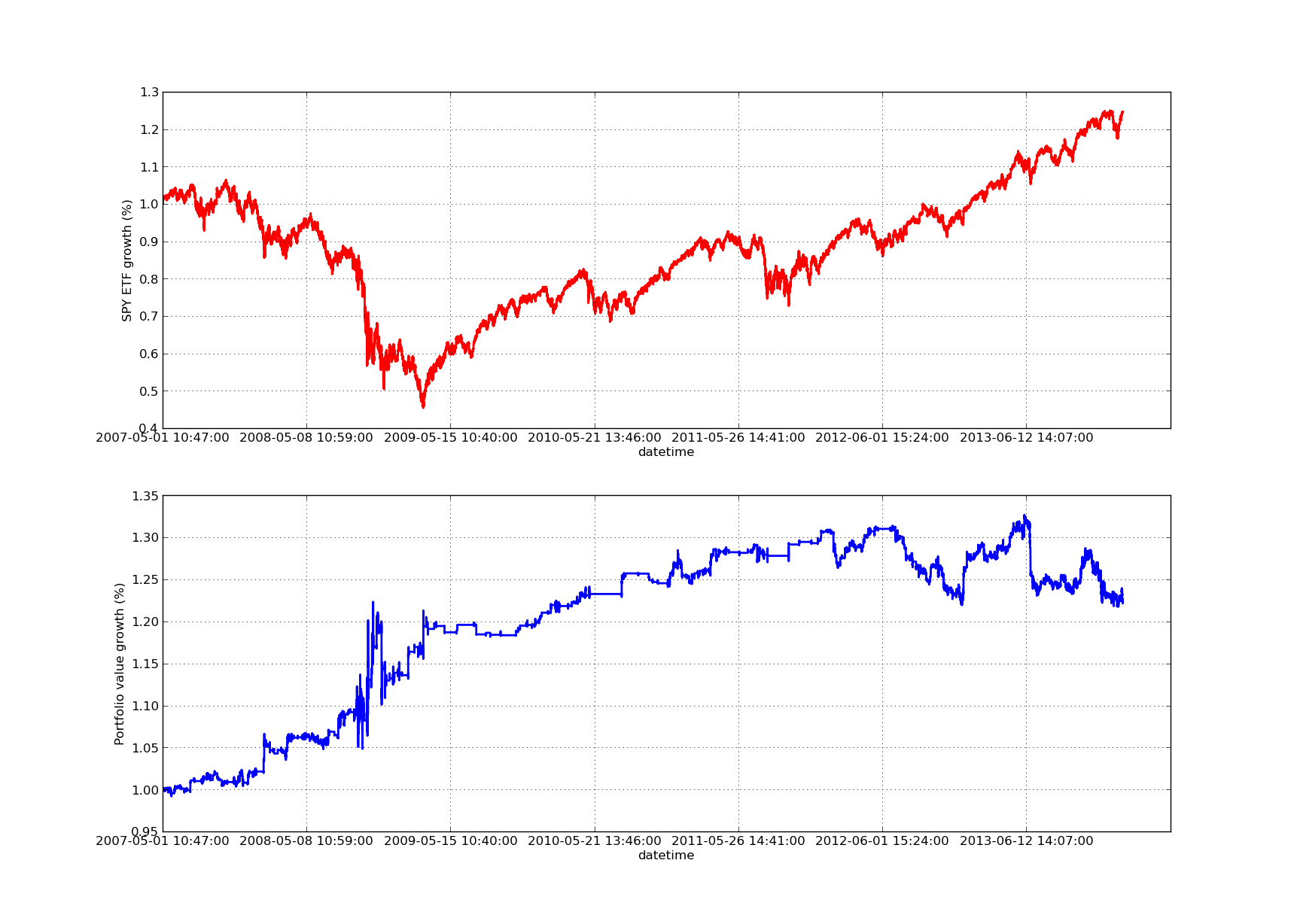
SPY-IWM Linear Regresi Lindung Nilai Nisbah Tinjau Balik Tempoh Analisis Sensitiviti

Ambil perhatian bahawa pengeluaran SPY agak besar pada tahun 2009 semasa krisis kewangan. Strategi ini juga berada dalam tempoh bergelora semasa fasa ini. Juga ambil perhatian bahawa prestasi telah merosot sepanjang tahun lepas disebabkan sifat SPY yang sangat trend dalam tempoh ini yang mencerminkan S&P 500.

Ambil perhatian bahawa kita masih perlu mengambil kira “kecondongan pandang ke hadapan” semasa mengira sebaran skor z. Tambahan pula, semua pengiraan ini dilakukan tanpa kos transaksi. Apabila faktor-faktor ini diambil kira, strategi ini pasti akan berprestasi buruk. Kedua-dua yuran dan slip pada masa ini tidak ditentukan. Selain itu, strategi berdagang dalam unit pecahan ETF, yang juga sangat tidak realistik.

Dalam artikel akan datang, kami akan mencipta penguji belakang terdorong peristiwa yang lebih kompleks yang akan mengambil kira semua perkara di atas, memberikan kami lebih keyakinan dalam keluk ekuiti dan penunjuk prestasi kami.