Perdagangan pasangan ialah contoh yang bagus untuk membangunkan strategi dagangan berdasarkan analisis matematik Dalam artikel ini, kami akan menunjukkan cara memanfaatkan data untuk mencipta dan mengautomasikan strategi dagangan pasangan.

Prinsip asas

Katakan anda mempunyai sepasang pelaburan X dan Y yang mempunyai beberapa korelasi asas, seperti kedua-dua syarikat yang mengeluarkan produk yang sama, seperti Pepsi dan Coca-Cola. Anda mahu nisbah harga atau asas (juga dipanggil spread) antara kedua-duanya kekal malar dari semasa ke semasa. Walau bagaimanapun, sebaran antara kedua-dua pasangan mungkin berbeza dari semasa ke semasa disebabkan oleh perubahan bekalan dan permintaan sementara, seperti pesanan beli/jual yang besar untuk satu sasaran pelaburan, reaksi terhadap berita penting tentang salah satu syarikat, dsb. Dalam kes ini, satu pelaburan bergerak ke atas dan satu lagi bergerak ke bawah berbanding satu sama lain. Jika anda menjangkakan perbezaan ini menjadi normal dari semasa ke semasa, anda boleh melihat peluang dagangan (atau peluang arbitraj). Peluang arbitraj sedemikian ada di mana-mana dalam pasaran mata wang digital atau pasaran niaga hadapan komoditi domestik, seperti hubungan antara BTC dan aset tempat selamat;

Apabila terdapat perbezaan harga sementara, perdagangan akan menjual pelaburan yang berprestasi tinggi (pelaburan yang telah meningkat) dan membeli pelaburan yang berprestasi rendah (pelaburan yang telah jatuh). spread akhirnya akan dicerminkan oleh pelaburan berprestasi yang menurun kembali atau pelaburan berprestasi rendah meningkat semula, atau kedua-duanya akan menghasilkan wang dalam semua senario ini. Jika pelaburan bergerak naik atau turun bersama-sama tanpa mengubah perbezaan antara mereka, anda tidak akan membuat atau kehilangan wang.

Oleh itu, dagangan pasangan ialah strategi dagangan neutral pasaran yang membolehkan pedagang mendapat keuntungan daripada hampir mana-mana keadaan pasaran: aliran menaik, aliran menurun atau sisi.

Terangkan konsep: dua sasaran pelaburan hipotesis

• Membina persekitaran penyelidikan kami pada Platform Kuantitatif Pencipta

Pertama sekali, untuk berfungsi dengan lancar, kami perlu membina persekitaran penyelidikan kami Dalam artikel ini, kami menggunakan Platform Kuantitatif Inventor (FMZ.COM) untuk membina persekitaran penyelidikan, terutamanya supaya kami boleh menggunakan API yang mudah dan pantas. antara muka dan enkapsulasi platform ini kemudiannya.

Atas nama rasmi Platform Kuantitatif Inventor, sistem Docker ini dipanggil sistem hos.

Untuk mendapatkan maklumat lanjut tentang cara menggunakan hos dan robot, sila rujuk artikel saya sebelum ini: https://www.fmz.com/bbs-topic/4140

Pembaca yang ingin membeli hos penggunaan pelayan pengkomputeran awan mereka sendiri boleh merujuk artikel ini: https://www.fmz.com/bbs-topic/2848

Selepas berjaya menggunakan perkhidmatan pengkomputeran awan dan sistem hos, kami akan memasang alat Python yang paling berkuasa: Anaconda

Untuk mencapai semua persekitaran program yang berkaitan yang diperlukan untuk artikel ini (pustaka bergantung, pengurusan versi, dll.), cara paling mudah ialah menggunakan Anaconda. Ia adalah ekosistem sains data Python yang dibungkus dan pengurus pergantungan.

Untuk kaedah pemasangan Anaconda, sila rujuk panduan rasmi Anaconda: https://www.anaconda.com/distribution/

Artikel ini juga akan menggunakan numpy dan panda, dua perpustakaan yang sangat popular dan penting dalam pengkomputeran saintifik Python.

Untuk kerja asas di atas, anda juga boleh merujuk artikel saya sebelum ini, yang memperkenalkan cara menyediakan persekitaran Anaconda dan dua perpustakaan numpy dan panda Untuk butiran, sila lihat: https://www.fmz.com/digest-. topik/4169

Seterusnya, mari kita gunakan kod untuk melaksanakan “dua sasaran pelaburan hipotesis”

import numpy as np
import pandas as pd

import statsmodels
from statsmodels.tsa.stattools import coint
# just set the seed for the random number generator
np.random.seed(107)

import matplotlib.pyplot as plt

Ya, kami juga akan menggunakan matplotlib, perpustakaan carta yang sangat terkenal dalam Python.

Mari jana aset pelaburan hipotesis X dan simulasi merancang pulangan hariannya menggunakan pengagihan normal. Kami kemudian melakukan jumlah kumulatif untuk mendapatkan nilai X harian.

# Generate daily returns
Xreturns = np.random.normal(0, 1, 100) 
# sum them and shift all the prices up
X = pd.Series(np.cumsum(
    Xreturns), name='X') 
    + 50
X.plot(figsize=(15,7))
plt.show()

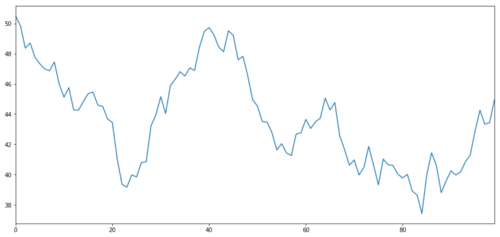
Sasaran pelaburan X, simulasi dan lukis pulangan hariannya melalui pengagihan normal

Sekarang kita menjana Y yang berkorelasi kuat dengan X, jadi harga Y sepatutnya bergerak hampir sama dengan perubahan dalam X. Kami memodelkan ini dengan mengambil X, menganjaknya ke atas, dan menambah beberapa hingar rawak yang diambil daripada taburan normal.

noise = np.random.normal(0, 1, 100)
Y = X + 5 + noise
Y.name = 'Y'
pd.concat([X, Y], axis=1).plot(figsize=(15,7))
plt.show()

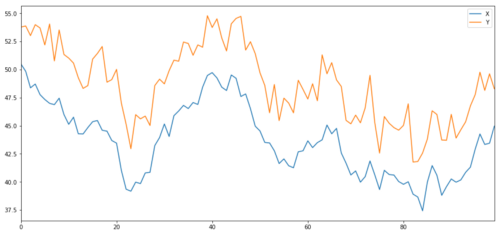
Menggabungkan sasaran pelaburan X dan Y

Kointegrasi

Kointegrasi sangat serupa dengan korelasi, bermakna nisbah antara dua siri data akan berbeza-beza di sekitar min Dua siri Y dan X mengikut yang berikut:

Y = ⍺ X + e

di mana ⍺ ialah nisbah malar dan e ialah bunyi.

Untuk pasangan dagangan antara dua siri masa, nilai jangkaan nisbah dari semasa ke semasa mesti menumpu kepada min, iaitu ia harus disatukan. Siri masa yang kami bina di atas disepadukan. Kami kini akan melukis skala antara kedua-duanya supaya kami dapat melihat bagaimana ia akan kelihatan.

(Y/X).plot(figsize=(15,7)) 
plt.axhline((Y/X).mean(), color='red', linestyle='--') 
plt.xlabel('Time')
plt.legend(['Price Ratio', 'Mean'])
plt.show()

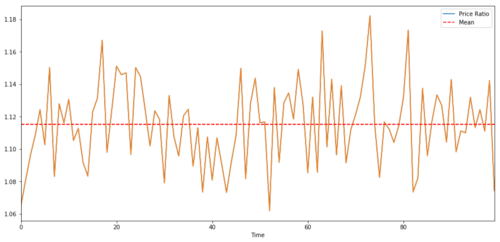
Nisbah dan purata harga dua pelaburan bersepadu

Ujian Kointegrasi

Cara mudah untuk menguji ini adalah dengan menggunakan statsmodels.tsa.stattools. Kita sepatutnya melihat nilai p yang sangat rendah kerana kita mencipta dua siri data secara buatan yang sepadu mungkin.

# compute the p-value of the cointegration test
# will inform us as to whether the ratio between the 2 timeseries is stationary
# around its mean
score, pvalue, _ = coint(X,Y)
print pvalue

Hasilnya ialah: 1.81864477307e-17

Nota: Korelasi dan Kointegrasi

Walaupun korelasi dan kointegrasi adalah serupa dalam teori, mereka tidak sama. Mari kita lihat contoh siri data yang berkorelasi tetapi tidak berkointegrasi, dan sebaliknya. Mula-mula mari kita semak korelasi siri yang baru kita hasilkan.

X.corr(Y)

Hasilnya ialah: 0.951

Seperti yang kita jangkakan, ini sangat tinggi. Tetapi bagaimana pula dengan dua siri yang berkorelasi tetapi tidak disatukan? Contoh mudah ialah dua siri data yang menyimpang.

ret1 = np.random.normal(1, 1, 100)
ret2 = np.random.normal(2, 1, 100)

s1 = pd.Series( np.cumsum(ret1), name='X')
s2 = pd.Series( np.cumsum(ret2), name='Y')

pd.concat([s1, s2], axis=1 ).plot(figsize=(15,7))
plt.show()
print 'Correlation: ' + str(X_diverging.corr(Y_diverging))
score, pvalue, _ = coint(X_diverging,Y_diverging)
print 'Cointegration test p-value: ' + str(pvalue)

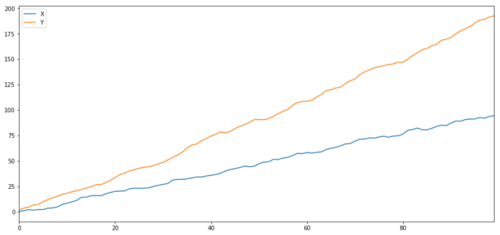
Dua siri berkaitan (tidak disepadukan bersama)

Pekali korelasi: 0.998 Nilai p ujian kointegrasi: 0.258

Contoh mudah kointegrasi tanpa korelasi ialah siri taburan normal dan gelombang persegi.

Y2 = pd.Series(np.random.normal(0, 1, 800), name='Y2') + 20
Y3 = Y2.copy()

Y3[0:100] = 30
Y3[100:200] = 10
Y3[200:300] = 30
Y3[300:400] = 10
Y3[400:500] = 30
Y3[500:600] = 10
Y3[600:700] = 30
Y3[700:800] = 10
Y2.plot(figsize=(15,7))
Y3.plot()
plt.ylim([0, 40])
plt.show()
# correlation is nearly zero
print 'Correlation: ' + str(Y2.corr(Y3))
score, pvalue, _ = coint(Y2,Y3)
print 'Cointegration test p-value: ' + str(pvalue)

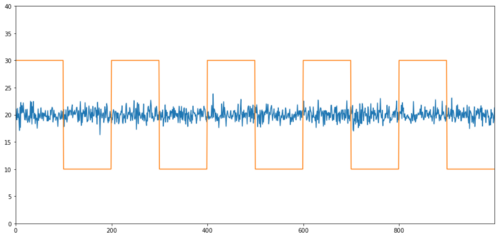
Korelasi: 0.007546 Ujian kointegrasi nilai-p: 0.0

Korelasi adalah sangat rendah, tetapi nilai p menunjukkan kointegrasi yang sempurna!

Bagaimana untuk melakukan perdagangan pasangan?

Oleh kerana dua siri masa bersepadu (seperti X dan Y di atas) bergerak ke arah dan menjauhi antara satu sama lain, ada kalanya terdapat asas tinggi dan asas rendah. Kami melakukan perdagangan pasangan dengan membeli satu pelaburan dan menjual yang lain. Dengan cara ini, jika kedua-dua sasaran pelaburan jatuh atau meningkat bersama-sama, kita tidak membuat wang atau kehilangan wang, iaitu, kita neutral pasaran.

Berbalik kepada X dan Y dalam Y = ⍺ X + e di atas, kita membuat wang dengan membuat nisbah (Y/X) bergerak di sekitar min ⍺ Untuk melakukan ini, kita perhatikan bahawa apabila X Apabila nilai ⍺ adalah terlalu tinggi atau terlalu rendah, nilai ⍺ terlalu tinggi atau terlalu rendah:

• Nisbah Panjang: Ini adalah apabila nisbah ⍺ kecil dan kami menjangkakan ia akan menjadi lebih besar. Dalam contoh di atas, kami membuka kedudukan dengan pergi panjang Y dan pendek X.

• Nisbah Pendek: Ini adalah apabila nisbah ⍺ adalah besar dan kami menjangkakan nisbah itu menjadi lebih kecil. Dalam contoh di atas, kami membuka kedudukan dengan memendekkan Y dan memanjang X.

Ambil perhatian bahawa kami sentiasa mempunyai “kedudukan lindung nilai”: jika belian asas kehilangan nilai, kedudukan jual menghasilkan wang, dan sebaliknya, jadi kami kebal terhadap pergerakan pasaran keseluruhan.

Apabila aset X dan Y bergerak secara relatif antara satu sama lain, kita memperoleh wang atau kehilangan wang.

Gunakan data untuk mencari urus niaga dengan tingkah laku yang serupa

Cara terbaik untuk melakukan ini ialah bermula dengan dagangan yang anda syak mungkin disatukan dan melakukan ujian statistik. Jika anda melakukan ujian statistik pada semua pasangan dagangan, anda akanBias perbandingan berbilangmangsa.

Bias perbandingan berbilangmerujuk kepada situasi di mana peluang untuk menghasilkan nilai p yang ketara meningkat apabila menjalankan banyak ujian, kerana kita perlu menjalankan sejumlah besar ujian. Jika kita menjalankan ujian ini 100 kali pada data rawak, kita akan melihat 5 nilai p di bawah 0.05. Jika anda membandingkan n instrumen untuk kointegrasi, anda akan melakukan perbandingan n(n-1)/2 dan anda akan melihat banyak nilai-p yang salah, yang akan meningkat apabila saiz sampel ujian anda bertambah Dan bertambah. Untuk mengelakkan perkara ini, pilih beberapa pasangan dagangan yang anda mempunyai sebab untuk percaya berkemungkinan akan disepadukan, dan kemudian mengujinya secara individu. Ini akan sangat mengurangkanBias perbandingan berbilang。

Jadi mari kita cuba mencari beberapa instrumen yang mempamerkan kointegrasi Mari kita ambil sekumpulan saham teknologi bermodal besar AS dalam S&P 500. Instrumen ini beroperasi dalam segmen pasaran yang serupa dan mempamerkan harga kointegrasi. Kami mengimbas senarai instrumen dagangan dan menguji kointegrasi antara semua pasangan.

Matriks skor ujian kointegrasi yang dikembalikan, matriks nilai p, dan semua padanan berpasangan dengan nilai p kurang daripada 0.05 disertakan.Kaedah ini terdedah kepada bias perbandingan berbilang, jadi dalam praktiknya mereka perlu melakukan pengesahan kedua. Dalam artikel ini, untuk kemudahan penjelasan kami, kami memilih untuk mengabaikan perkara ini dalam contoh.

def find_cointegrated_pairs(data):
    n = data.shape[1]
    score_matrix = np.zeros((n, n))
    pvalue_matrix = np.ones((n, n))
    keys = data.keys()
    pairs = []
    for i in range(n):
        for j in range(i+1, n):
            S1 = data[keys[i]]
            S2 = data[keys[j]]
            result = coint(S1, S2)
            score = result[0]
            pvalue = result[1]
            score_matrix[i, j] = score
            pvalue_matrix[i, j] = pvalue
            if pvalue < 0.02:
                pairs.append((keys[i], keys[j]))
    return score_matrix, pvalue_matrix, pairs

Nota: Kami telah memasukkan penanda aras pasaran (SPX) dalam data kami - pasaran memacu aliran banyak instrumen dan selalunya anda mungkin menemui dua instrumen yang nampaknya disatukan tetapi sebenarnya ia tidak disatukan antara satu sama lain, tetapi Kointegrasi dengan pasaran. Ini dipanggil pembolehubah mengelirukan. Adalah penting untuk memeriksa penyertaan pasaran dalam mana-mana hubungan yang anda temui.

from backtester.dataSource.yahoo_data_source import YahooStockDataSource
from datetime import datetime
startDateStr = '2007/12/01'
endDateStr = '2017/12/01'
cachedFolderName = 'yahooData/'
dataSetId = 'testPairsTrading'
instrumentIds = ['SPY','AAPL','ADBE','SYMC','EBAY','MSFT','QCOM',
                 'HPQ','JNPR','AMD','IBM']
ds = YahooStockDataSource(cachedFolderName=cachedFolderName,
                            dataSetId=dataSetId,
                            instrumentIds=instrumentIds,
                            startDateStr=startDateStr,
                            endDateStr=endDateStr,
                            event='history')
data = ds.getBookDataByFeature()['Adj Close']
data.head(3)

Sekarang marilah kita cuba mencari pasangan dagangan terintegrasi menggunakan kaedah kami.

# Heatmap to show the p-values of the cointegration test
# between each pair of stocks
scores, pvalues, pairs = find_cointegrated_pairs(data)
import seaborn
m = [0,0.2,0.4,0.6,0.8,1]
seaborn.heatmap(pvalues, xticklabels=instrumentIds, 
                yticklabels=instrumentIds, cmap=’RdYlGn_r’, 
                mask = (pvalues >= 0.98))
plt.show()
print pairs

[('ADBE', 'MSFT')]

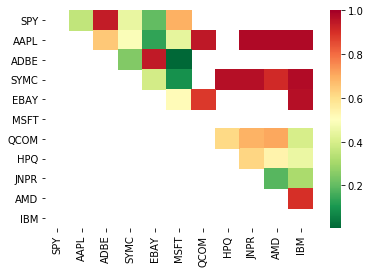
Nampaknya ‘ADBE’ dan ‘MSFT’ disatukan. Mari kita lihat harga untuk memastikan ia benar-benar masuk akal.

S1 = data['ADBE']
S2 = data['MSFT']
score, pvalue, _ = coint(S1, S2)
print(pvalue)
ratios = S1 / S2
ratios.plot()
plt.axhline(ratios.mean())
plt.legend([' Ratio'])
plt.show()

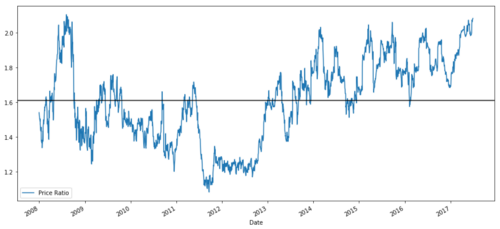
Carta nisbah harga antara MSFT dan ADBE dari 2008 hingga 2017

Nisbah ini kelihatan seperti purata yang stabil. Nisbah mutlak tidak begitu berguna secara statistik. Adalah lebih berguna untuk menormalkan isyarat kami dengan melihatnya sebagai skor z. Skor Z ditakrifkan sebagai:

Z Score (Value) = (Value — Mean) / Standard Deviation

memberi amaran

Dalam amalan, kami biasanya cuba menggunakan beberapa pengembangan pada data, tetapi hanya jika data diedarkan secara normal. Walau bagaimanapun, banyak data kewangan tidak diedarkan secara normal, jadi kita mesti berhati-hati untuk tidak menganggap normaliti atau sebarang taburan tertentu semasa menjana statistik. Taburan nisbah sebenar mungkin mempunyai ekor yang gemuk, dan data yang cenderung ke arah ekstrem boleh mengelirukan model kami dan membawa kepada kerugian besar.

def zscore(series):
    return (series - series.mean()) / np.std(series)

zscore(ratios).plot()
plt.axhline(zscore(ratios).mean())
plt.axhline(1.0, color=’red’)
plt.axhline(-1.0, color=’green’)
plt.show()

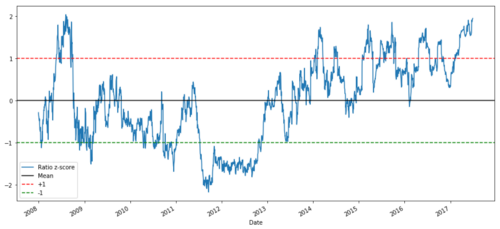
Nisbah Harga Z antara MSFT dan ADBE dari 2008 hingga 2017

Kini lebih mudah untuk melihat bagaimana nisbah bergerak di sekitar min, tetapi kadangkala ia cenderung mempunyai sisihan besar daripada min, yang boleh kita eksploitasi.

Sekarang setelah kita membincangkan asas strategi perdagangan pasangan dan mengenal pasti sasaran penyepaduan bersama berdasarkan sejarah harga, mari cuba membangunkan isyarat dagangan. Mula-mula, mari kita semak langkah-langkah untuk membangunkan isyarat dagangan menggunakan teknik data:

• Mengumpul data yang boleh dipercayai dan membersihkan data

• Cipta fungsi daripada data untuk mengenal pasti isyarat/logik dagangan

• Ciri boleh menjadi purata bergerak atau data harga, korelasi atau nisbah isyarat yang lebih kompleks - gabungkan ini untuk mencipta ciri baharu

• Gunakan ciri-ciri ini untuk menjana isyarat dagangan, iaitu isyarat beli, jual atau jual beli

Nasib baik, kami mempunyai Platform Kuantitatif Inventor (fmz.com) untuk melengkapkan empat aspek di atas untuk kami. Ini adalah rahmat yang besar untuk pembangun strategi.

Pada Platform Kuantitatif Pencipta, terdapat antara muka berpakej pelbagai pertukaran arus perdana yang perlu kita lakukan ialah memanggil antara muka API ini Selebihnya logik pelaksanaan asas telah digilap oleh pasukan profesional.

Demi kesempurnaan logik dan penjelasan prinsip, kami akan membentangkan logik asas ini secara terperinci, tetapi dalam operasi sebenar, pembaca boleh terus menghubungi antara muka API Inventor Quant untuk melengkapkan empat aspek di atas.

Mari mulakan:

Langkah 1: Sediakan masalah anda

Di sini kami cuba mencipta isyarat yang memberitahu kami sama ada nisbah itu akan menjadi beli atau jual pada masa seterusnya, iaitu pembolehubah peramal kami Y:

Y = Ratio is buy (1) or sell (-1)

Y(t)= Sign(Ratio(t+1) — Ratio(t))

Ambil perhatian bahawa kita tidak perlu meramalkan harga sebenar aset pendasar, malah nilai sebenar nisbah (walaupun boleh), kita hanya perlu meramalkan arah nisbah seterusnya.

Langkah 2: Kumpul data yang boleh dipercayai dan tepat

Inventor Quant ialah rakan anda! Anda hanya tentukan instrumen yang anda ingin berdagang dan sumber data yang anda mahu gunakan, dan ia akan mengekstrak data yang diperlukan dan membersihkannya untuk pembahagian dividen dan instrumen. Jadi data kami di sini sudah sangat bersih.

Kami menggunakan data berikut daripada Yahoo Finance untuk hari dagangan sepanjang 10 tahun yang lalu (kira-kira 2,500 titik data): buka, tutup, tinggi, rendah dan volum

Langkah 3: Pisahkan data

Jangan lupa langkah yang sangat penting ini untuk menguji ketepatan model anda. Kami menggunakan pembahagian tren/pengesahan/ujian data berikut

• Training 7 years ~ 70%

• Test ~ 3 years 30%

ratios = data['ADBE'] / data['MSFT']
print(len(ratios))
train = ratios[:1762]
test = ratios[1762:]

Sebaik-baiknya, kami juga akan membuat set pengesahan, tetapi kami tidak akan melakukannya buat masa ini.

Langkah 4: Kejuruteraan Ciri

Apakah fungsi yang berkaitan? Kami ingin meramalkan arah perubahan nisbah. Kami telah melihat bahawa kedua-dua instrumen kami disatukan, jadi nisbah ini akan cenderung beralih dan kembali kepada min. Nampaknya ciri kami sepatutnya menjadi beberapa ukuran min nisbah, dan perbezaan antara nilai semasa dan min boleh menjana isyarat dagangan kami.

Kami menggunakan fungsi berikut:

• Nisbah Purata Pergerakan 60 Hari: Ukuran purata bergolek

• Nisbah Purata Pergerakan 5 Hari: Ukuran nilai semasa purata

• sisihan piawai 60 hari

• z-skor: (5d MA - 60d MA) / 60d SD

ratios_mavg5 = train.rolling(window=5,
                               center=False).mean()
ratios_mavg60 = train.rolling(window=60,
                               center=False).mean()
std_60 = train.rolling(window=60,
                        center=False).std()
zscore_60_5 = (ratios_mavg5 - ratios_mavg60)/std_60
plt.figure(figsize=(15,7))
plt.plot(train.index, train.values)
plt.plot(ratios_mavg5.index, ratios_mavg5.values)
plt.plot(ratios_mavg60.index, ratios_mavg60.values)
plt.legend(['Ratio','5d Ratio MA', '60d Ratio MA'])
plt.ylabel('Ratio')
plt.show()

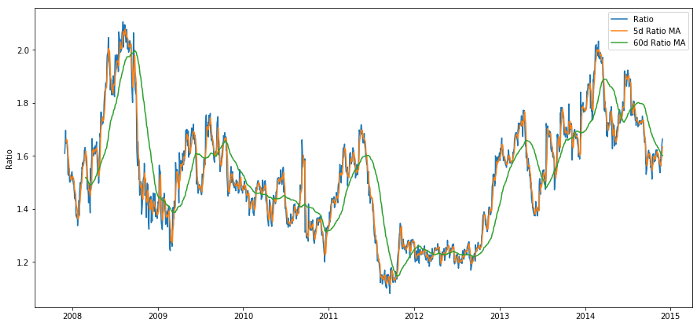
Nisbah harga 60d dan 5d MA

plt.figure(figsize=(15,7))
zscore_60_5.plot()
plt.axhline(0, color='black')
plt.axhline(1.0, color='red', linestyle='--')
plt.axhline(-1.0, color='green', linestyle='--')
plt.legend(['Rolling Ratio z-Score', 'Mean', '+1', '-1'])
plt.show()

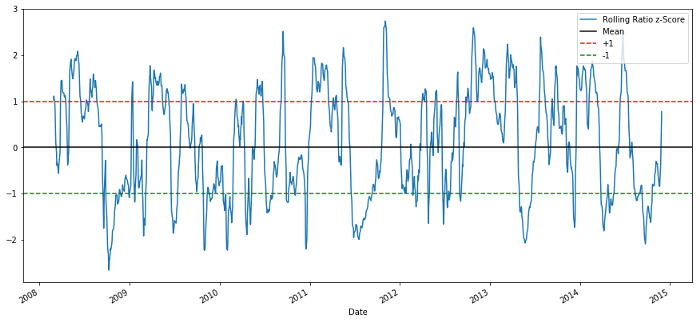
60-5 Z-skor Nisbah Harga

Skor Z bagi min rolling benar-benar menunjukkan sifat pembalikan min bagi nisbah!

Langkah 5: Pemilihan model

Mari kita mulakan dengan model yang sangat mudah. Melihat pada graf skor-z, kita dapat melihat bahawa apabila skor-z terlalu tinggi atau terlalu rendah, ia akan mundur. Mari gunakan +1/-1 sebagai ambang kita untuk menentukan terlalu tinggi dan terlalu rendah, kemudian kita boleh menggunakan model berikut untuk menjana isyarat dagangan:

• Apabila z di bawah -1.0, nisbahnya ialah beli (1) kerana kita menjangkakan z akan kembali kepada 0, jadi nisbahnya meningkat

• Apabila z melebihi 1.0, nisbahnya ialah jual (-1) kerana kami menjangkakan z kembali kepada 0, sekali gus mengurangkan nisbah

Langkah 6: Latihan, Pengesahan dan Pengoptimuman

Akhir sekali, mari kita lihat kesan sebenar model kami pada data sebenar? Mari lihat bagaimana isyarat ini berkelakuan dalam nisbah sebenar

# Plot the ratios and buy and sell signals from z score
plt.figure(figsize=(15,7))
train[60:].plot()
buy = train.copy()
sell = train.copy()
buy[zscore_60_5>-1] = 0
sell[zscore_60_5<1] = 0
buy[60:].plot(color=’g’, linestyle=’None’, marker=’^’)
sell[60:].plot(color=’r’, linestyle=’None’, marker=’^’)
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,ratios.min(),ratios.max()))
plt.legend([‘Ratio’, ‘Buy Signal’, ‘Sell Signal’])
plt.show()

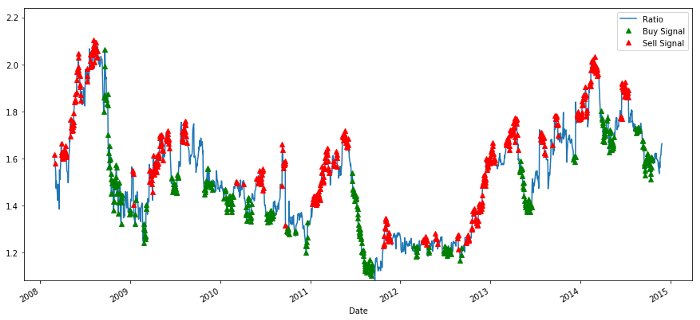
Isyarat Nisbah Harga Beli dan Jual

Isyarat ini kelihatan munasabah, kita seolah-olah menjual nisbah apabila ia tinggi atau meningkat (titik merah) dan membelinya semula apabila ia rendah (titik hijau) dan menurun. Apakah maksud ini untuk perkara sebenar urus niaga kami? jom tengok

# Plot the prices and buy and sell signals from z score
plt.figure(figsize=(18,9))
S1 = data['ADBE'].iloc[:1762]
S2 = data['MSFT'].iloc[:1762]
S1[60:].plot(color='b')
S2[60:].plot(color='c')
buyR = 0*S1.copy()
sellR = 0*S1.copy()
# When buying the ratio, buy S1 and sell S2
buyR[buy!=0] = S1[buy!=0]
sellR[buy!=0] = S2[buy!=0]
# When selling the ratio, sell S1 and buy S2 
buyR[sell!=0] = S2[sell!=0]
sellR[sell!=0] = S1[sell!=0]
buyR[60:].plot(color='g', linestyle='None', marker='^')
sellR[60:].plot(color='r', linestyle='None', marker='^')
x1,x2,y1,y2 = plt.axis()
plt.axis((x1,x2,min(S1.min(),S2.min()),max(S1.max(),S2.max())))
plt.legend(['ADBE','MSFT', 'Buy Signal', 'Sell Signal'])
plt.show()

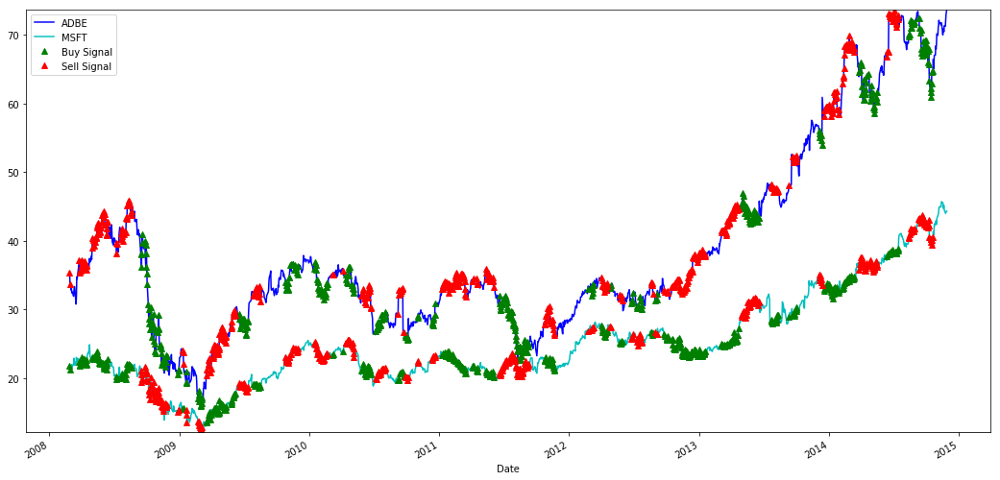
Isyarat untuk membeli dan menjual saham MSFT dan ADBE

Perhatikan bagaimana kita kadang-kadang membuat wang dengan “kaki pendek”, kadang-kadang pada “kaki panjang”, dan kadang-kadang kedua-duanya.

Kami gembira dengan isyarat data latihan. Mari lihat apakah jenis keuntungan yang boleh dihasilkan oleh isyarat ini. Kami boleh membuat penguji belakang mudah yang membeli 1 nisbah (membeli 1 saham ADBE dan menjual nisbah x saham MSFT) apabila nisbahnya rendah dan menjual 1 nisbah (menjual 1 saham ADBE dan nisbah panggilan x saham MSFT) dan mengira dagangan PnL untuk ini nisbah.

# Trade using a simple strategy
def trade(S1, S2, window1, window2):
    
    # If window length is 0, algorithm doesn't make sense, so exit
    if (window1 == 0) or (window2 == 0):
        return 0
    
    # Compute rolling mean and rolling standard deviation
    ratios = S1/S2
    ma1 = ratios.rolling(window=window1,
                               center=False).mean()
    ma2 = ratios.rolling(window=window2,
                               center=False).mean()
    std = ratios.rolling(window=window2,
                        center=False).std()
    zscore = (ma1 - ma2)/std
    
    # Simulate trading
    # Start with no money and no positions
    money = 0
    countS1 = 0
    countS2 = 0
    for i in range(len(ratios)):
        # Sell short if the z-score is > 1
        if zscore[i] > 1:
            money += S1[i] - S2[i] * ratios[i]
            countS1 -= 1
            countS2 += ratios[i]
            print('Selling Ratio %s %s %s %s'%(money, ratios[i], countS1,countS2))
        # Buy long if the z-score is < 1
        elif zscore[i] < -1:
            money -= S1[i] - S2[i] * ratios[i]
            countS1 += 1
            countS2 -= ratios[i]
            print('Buying Ratio %s %s %s %s'%(money,ratios[i], countS1,countS2))
        # Clear positions if the z-score between -.5 and .5
        elif abs(zscore[i]) < 0.75:
            money += S1[i] * countS1 + S2[i] * countS2
            countS1 = 0
            countS2 = 0
            print('Exit pos %s %s %s %s'%(money,ratios[i], countS1,countS2))
            
            
    return money
trade(data['ADBE'].iloc[:1763], data['MSFT'].iloc[:1763], 60, 5)

Hasilnya ialah: 1783.375

Jadi strategi ini nampaknya menguntungkan! Kini, kami boleh mengoptimumkan lagi dengan menukar tetingkap masa purata bergerak, dengan menukar ambang untuk beli/jual dan tutup kedudukan, dsb. dan menyemak peningkatan prestasi pada data pengesahan.

Kami juga boleh mencuba model yang lebih kompleks seperti Regresi Logistik, SVM, dsb. untuk 1/-1 ramalan.

Sekarang, mari kita memajukan model ini, yang membawa kita kepada

Langkah 7: Uji balik data ujian

Di sini saya ingin menyebut Platform Kuantitatif Pencipta Ia menggunakan enjin ujian belakang QPS/TPS berprestasi tinggi untuk benar-benar menghasilkan semula persekitaran sejarah, menghapuskan perangkap ujian belakang kuantitatif yang biasa, dan segera menemui kelemahan strategi, supaya dapat memberikan yang sebenar dengan lebih baik. -pelaburan masa.

Untuk menjelaskan prinsip, artikel ini memilih untuk menunjukkan logik asas Dalam aplikasi praktikal, adalah disyorkan bahawa pembaca menggunakan Platform Kuantitatif Inventor Selain menjimatkan masa, perkara penting adalah untuk meningkatkan kadar toleransi kesalahan.

Ujian belakang adalah mudah. ​​Kita boleh menggunakan fungsi di atas untuk melihat PnL data ujian.

trade(data[‘ADBE’].iloc[1762:], data[‘MSFT’].iloc[1762:], 60, 5)

Hasilnya ialah: 5262.868

Model ini dibuat dengan sangat baik! Ia menjadi model dagangan pasangan mudah pertama kami.

Elakkan overfitting

Sebelum saya mengakhiri, saya ingin bercakap secara khusus tentang overfitting. Overfitting adalah perangkap paling berbahaya dalam strategi perdagangan. Algoritma overfitting mungkin berprestasi sangat baik dalam ujian belakang tetapi gagal pada data ghaib baharu - bermakna ia tidak benar-benar mendedahkan sebarang arah aliran dalam data dan tidak mempunyai kuasa ramalan sebenar. Mari kita ambil contoh mudah.

Dalam model kami, kami menggunakan anggaran parameter rolling dan berharap dapat mengoptimumkan panjang tetingkap masa. Kami mungkin memutuskan untuk hanya mengulangi semua kemungkinan, panjang tetingkap masa yang munasabah dan memilih tempoh masa berdasarkan model kami berprestasi terbaik. Di bawah kami menulis gelung mudah untuk menjaringkan panjang tetingkap masa berdasarkan PNL data latihan dan mencari gelung terbaik.

# Find the window length 0-254 
# that gives the highest returns using this strategy
length_scores = [trade(data['ADBE'].iloc[:1762], 
                data['MSFT'].iloc[:1762], l, 5) 
                for l in range(255)]
best_length = np.argmax(length_scores)
print ('Best window length:', best_length)

('Best window length:', 40)

Sekarang kami menyemak prestasi model pada data ujian, dan kami melihat bahawa panjang tetingkap kali ini jauh dari optimum! Ini kerana pilihan asal kami jelas mengatasi data sampel.

# Find the returns for test data
# using what we think is the best window length
length_scores2 = [trade(data['ADBE'].iloc[1762:], 
                  data['MSFT'].iloc[1762:],l,5) 
                  for l in range(255)]
print (best_length, 'day window:', length_scores2[best_length])
# Find the best window length based on this dataset, 
# and the returns using this window length
best_length2 = np.argmax(length_scores2)
print (best_length2, 'day window:', length_scores2[best_length2])

(40, 'day window:', 1252233.1395)
(15, 'day window:', 1449116.4522)

Jelas sekali perkara yang berfungsi dengan baik untuk data sampel kami tidak selalu menghasilkan hasil yang baik pada masa hadapan. Hanya untuk ujian, mari kita plot skor panjang yang dikira daripada dua set data

plt.figure(figsize=(15,7))
plt.plot(length_scores)
plt.plot(length_scores2)
plt.xlabel('Window length')
plt.ylabel('Score')
plt.legend(['Training', 'Test'])
plt.show()

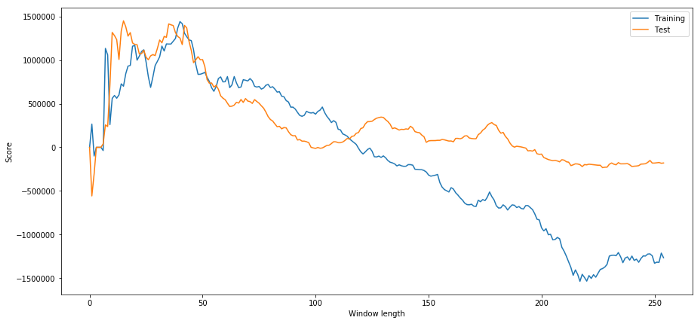
Kita dapat melihat bahawa apa-apa antara 20-50 adalah pilihan yang baik untuk tetingkap masa.

Untuk mengelakkan overfitting, kita boleh menggunakan penaakulan ekonomi atau sifat algoritma untuk memilih panjang tetingkap masa. Kami juga boleh menggunakan penapis Kalman, yang tidak memerlukan kami untuk menentukan panjang kaedah ini akan dibincangkan kemudian dalam artikel lain.

Langkah seterusnya

Dalam artikel ini, kami membentangkan beberapa kaedah pengenalan mudah untuk menunjukkan proses membangunkan strategi perdagangan. Dalam amalan, statistik yang lebih canggih harus digunakan, dan anda boleh mempertimbangkan pilihan berikut:

• Eksponen Hurst

• Separuh hayat pembalikan min disimpulkan daripada proses Ornstein-Uhlenbeck

• Penapis Kalman