Mengapa analisis teknikal tradisional gagal dalam pasaran yang kompleks?

Dalam bidang perdagangan kuantitatif, kita sering mengalami kekeliruan: mengapa strategi berdasarkan purata bergerak sederhana atau RSI berprestasi dalam keadaan pasaran tertentu, tetapi sering gagal dalam keadaan pasaran lain? Jawapannya terletak pada kerumitan urutan masa kewangan - mereka tidak hanya mempunyai hubungan diri, tetapi juga ciri-ciri kadar turun naik yang berubah mengikut masa.

Strategi yang akan kita bincangkan hari ini, dengan kecerdasan menggabungkan model regresi AR ((2)) dan model kecacatan berkondisi GARCH ((1,1)), cuba menyelesaikan masalah ini dari sudut statistik. Ini bukan sekadar penumpukan petunjuk teknikal, tetapi penggalian mendalam mengenai ciri-ciri asas siri masa kewangan.

Bagaimana model ini menangkap kesan ingatan harga?

Strategi ini berpusat pada penggunaan model autoregresi AR[2]: apa itu autoregresi? Secara ringkasnya, ia adalah menggunakan masa lalu untuk meramalkan masa depan. Model AR[2] mengandaikan bahawa kadar pulangan semasa dapat diwakili secara linear oleh kadar pulangan dua tempoh sebelumnya:

            
            
            
r_t = φ₁ × r_{t-1} + φ₂ × r_{t-2} + ε_t

Kode ini menggunakan persamaan Yule-Walker untuk menyelesaikan faktor φ1 dan φ2:

            pinescript
            
            
c0 = calcAutoCovariance(returns, 0, lengthReg) // 滞后0期自协方差
c1 = calcAutoCovariance(returns, 1, lengthReg) // 滞后1期自协方差  
c2 = calcAutoCovariance(returns, 2, lengthReg) // 滞后2期自协方差
phi1 = (c1 * c0 - c2 * c1) / denominator // 第一个自回归系数
phi2 = (c2 * c0 - c1 * c1) / denominator // 第二个自回归系数

Kelebihan kaedah ini adalah bahawa ia tidak bergantung kepada penilaian subjektif, tetapi membiarkan data itu sendiri "bercakap" dan menemui keteraturan yang tersirat dalam urutan harga.

Mengapa model GARCH lebih baik dalam menggambarkan risiko pasaran?

Model AR sahaja tidak mencukupi, kerana kadar turun naik pasaran kewangan tidak tetap. Kita semua tahu bahawa fenomena "kumpulan kadar turun naik" - apabila turun naik yang besar sering disertai dengan turun naik yang besar, keadaan tenang sering berlangsung lebih lama.

Model GARCH ((1,1) adalah untuk menggambarkan ciri-ciri ini:

            
            
            
σ²_t = ω + α × ε²_{t-1} + β × σ²_{t-1}

Ini jelas ditunjukkan oleh logik pelaksanaan dalam kod:

            pinescript
            
            
omega = (1 - adjustedAlpha - adjustedBeta) * longTermVar
garchVariance := omega + adjustedAlpha * math.pow(arResidual[1], 2) + adjustedBeta * garchVariance[1]

Wawasan utama di sini ialah: keadaan semasa hampir bergantung kepada sisa kuadrat masa lalu ((kesan jangka pendek), tetapi juga bergantung kepada keadaan keadaan masa lalu ((kesan jangka panjang). Parameter α mengawal kesan kejutan jangka pendek, β mengawal kekebalan kadar turun naik.

Bagaimana logik perdagangan strategi ini dapat menyeimbangkan risiko dan faedah?

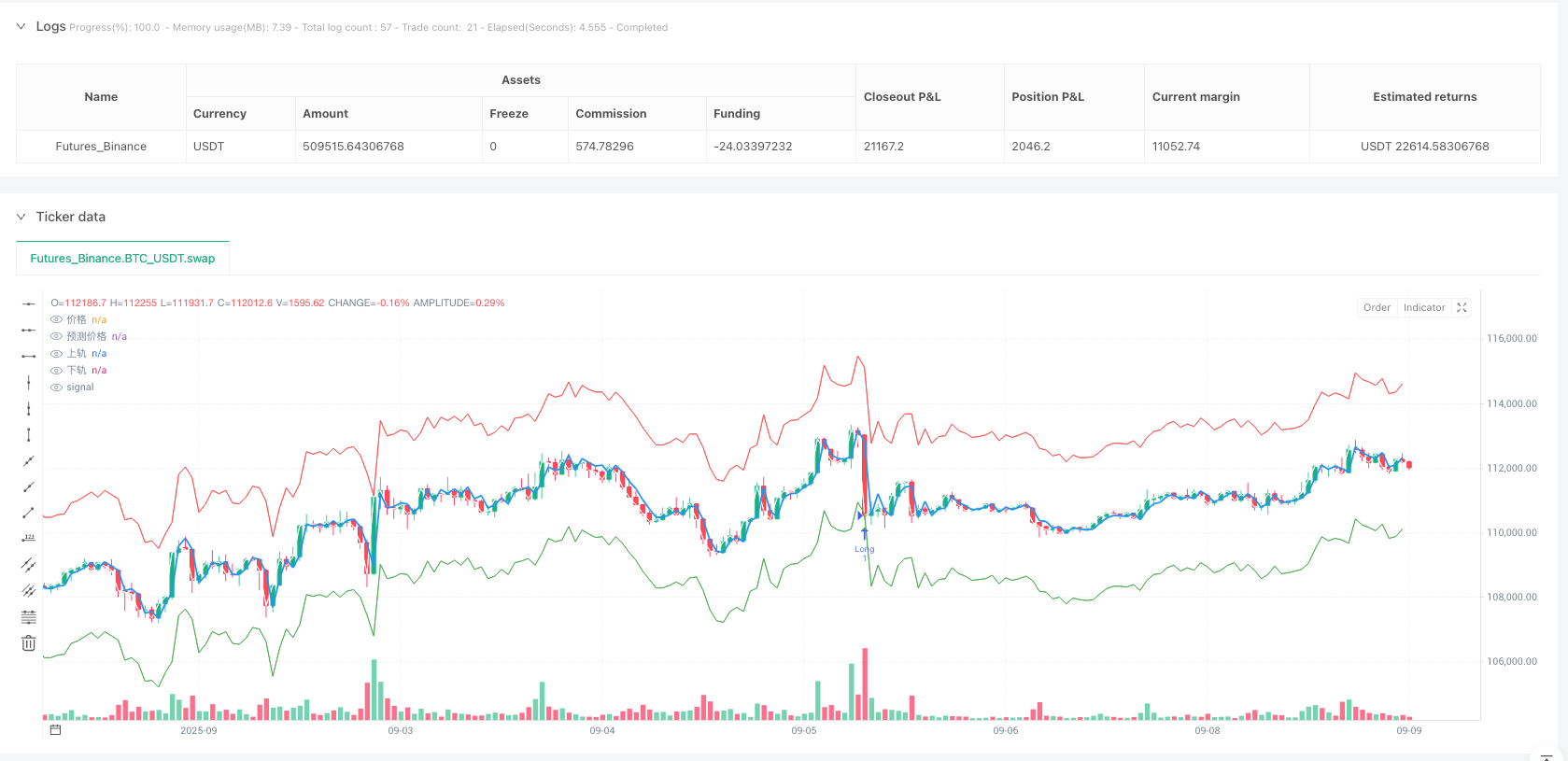
Dengan unjuran AR dan unjuran GARCH, strategi ini membina selang keyakinan yang dinamik:

            pinescript
            
            
upperReturnBand = arReturnPredict + stdevFactor * garchStd
lowerReturnBand = arReturnPredict - stdevFactor * garchStd

Logik penjanaan isyarat dagangan mencerminkan idea regresi rata-rata:

• Apabila harga turun ke bawah (longSignal = rawPrice < lowerPriceBand)
• Apabila harga menembusi upperBand (shortSignal = rawPrice > upperPriceBand)

Ciri-ciri reka bentuk ini ialah: lebar jurang keyakinan akan disesuaikan dengan kadar turun naik pasaran yang dinamik. Pada masa turun naik yang tinggi, jurang menjadi lebih lebar, mengurangkan frekuensi perdagangan; pada masa turun naik yang rendah, jurang menjadi lebih sempit, meningkatkan peluang perdagangan.

Apa yang perlu diperhatikan dalam aplikasi sebenar?

1. Ujian kestabilan model
Kod ini mengandungi pemeriksaan kestabilan yang penting:

            pinescript
            
            
if stabilityCheck >= 0.99 or math.abs(phi2) >= 0.99
    scaleFactor = 0.95 / math.max(stabilityCheck, math.abs(phi2) + 0.01)

Ini memastikan model AR stabil dan mengelakkan hasil ramalan yang terbelah.

2. Ketetapan kekeruhan parameter
Model GARCH memerlukan α + β < 1 untuk menjamin perbezaan jangka panjang:

            pinescript
            
            
if sumParam >= 0.999
    scale = 0.99 / sumParam

3. Keperluan untuk mekanisme penapisan
Strategi menyediakan pilihan penapisan RSI, yang penting dalam aplikasi praktikal. Model statistik semata-mata mungkin mengabaikan ciri-ciri trend pasaran, dan penambahan penunjuk teknikal dapat memberikan isyarat pengesahan tambahan.

Batasan strategi dan cara untuk diperbaiki

Walaupun strategi ini elegan dalam teori, ia perlu dipertimbangkan dalam aplikasi:

Pilihan frekuensi dataModel AR-GARCH mempunyai perbezaan yang besar dalam prestasi dalam tempoh yang berbeza. Data frekuensi tinggi memberikan lebih banyak maklumat, tetapi juga memperkenalkan lebih banyak kebisingan.

Perubahan masa parameterRealisasi semasa mengandaikan parameter AR dan GARCH tetap dalam tetingkap anggaran, tetapi struktur pasaran sebenar mungkin berubah.

Kesan kos urus niagaStrategi arbitraj statistik biasanya memerlukan frekuensi dagangan yang lebih tinggi, dan kos bayaran dan slippage tidak boleh diabaikan.

Kesimpulannya: Nilai Pemodelan Statistik dalam Pertukaran Kuantitatif

Strategi AR-GARCH ini menunjukkan kekuatan statistik moden dalam pemodelan kewangan. Ia bukan sekadar gabungan petunjuk teknikal, tetapi penggalian mendalam mengenai ciri statistik siri masa kewangan.

Bagi peniaga kuantitatif, keharusan untuk memahami strategi seperti ini bukan hanya dalam aplikasi langsung, tetapi juga dalam kemahiran untuk menganalisis pasaran dengan pemikiran statistik. Dengan AI dan pembelajaran mesin yang meluas hari ini, model statistik klasik ini masih menjadi asas penting untuk memahami pasaran dan membina strategi.