Neste artigo, vamos descrever o processo Ornstein-Uhlenbeck, descrever a sua fórmula matemática, implementá-lo e simular com Python, e discutir algumas aplicações práticas em finanças quantitativas e transações de sistemas. Usaremos um modelo de processo aleatório mais avançado, chamado processo Ornstein-Uhlenbeck (OU), que pode ser usado para modelar sequências de tempo de regressão que exibem um comportamento de equivalência.

O que é o Processo Ornstein-Uhlenbeck?

O processo de Ornstein-Uhlenbeck é um processo de aleatoriedade de tempo contínuo usado para modelar o comportamento de regressão de equivalência. Isso significa que, ao contrário do padrão de corridas aleatórias ou movimentos de Brown, que podem ser desviados infinitamente, o processo de OU tende a se recuperar ao longo do tempo para a média de longo prazo. Em termos matemáticos, o processo de OU é a solução de uma equação de diferenciação aleatória específica (SDE) que controla esse comportamento de regressão de equivalência. O SDE do processo de OU é dado pela seguinte fórmula:

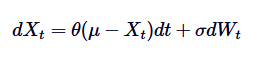
Dentre eles, Xt representa um processo aleatório em tempo t, μ é a média a longo prazo, θ é a taxa de regressão à média, δ é a volatilidade, e dWt é o processo de Wiener ou o movimento padrão de Brown.

Contexto histórico e aplicações

O processo de Ornstein-Uhlenbeck foi originalmente proposto por Leonard Ornstein e George Eugene Uhlenbeck em 1930 para simular a velocidade de partículas em movimento Browniano em condições de fricção. Com o passar do tempo, suas aplicações foram muito além da física, com aplicações em diferentes áreas, como biologia, química, economia e finanças.

Na finança quantitativa, o processo OU é especialmente útil para modelar o fenômeno que demonstra a regressão do valor médio. Exemplos notáveis incluem a volatilidade das taxas de juros, taxas de câmbio e mercados financeiros. Por exemplo, o popular modelo de taxas de juros, o modelo Vasicek, é derivado diretamente do processo OU.

Importância na finança quântica

O processo de Ornstein-Uhlenbeck é fundamental na finança quantitativa, porque sua natureza de regressão de média torna-a uma escolha natural para a modelagem de variáveis financeiras que não apresentam um comportamento de deslocamento aleatório, mas sim uma oscilação de média em torno de uma estabilidade de longo prazo. Esta característica é fundamental para a modelagem de taxas de juros, em que a regressão de média reflete a influência dos bancos centrais sobre a estabilidade de longo prazo.

Além disso, o processo OU também é usado em modelos de preços de ativos (incluindo a avaliação de derivativos) e estratégias de gerenciamento de risco. Também pode ser usado como bloco de construção de modelos mais complexos, como o modelo Cox-Ingersoll-Ross (CIR), que amplia o processo OU para a modelagem de taxas de juros com valores não negativos.

Principais características e intuição

As principais características do processo Ornstein-Uhlenbeck podem ser resumidas como segue:

• Regressão média:O processo OU tende a regressar à média de longo prazo μ. Isto contrasta com processos como o movimento de Brown, que não apresentam essa tendência.
• Variação:O parâmetro δ é o nível de aleatoriedade ou volatilidade no processo de controle. Quanto maior a volatilidade, maior o desvio do processo do valor médio antes da regressão.
• Velocidade de regresso:O parâmetro θ determina a velocidade com que o processo retorna ao valor médio. Quanto maior o valor θ, mais rápido é o retorno ao valor médio.
• Estabilidade:O processo OU é estável, o que significa que suas características estatísticas não mudam com o tempo. Isso é fundamental para a modelagem de sistemas estáveis no setor financeiro.

Intuitivamente falando, você pode considerar o processo de Ornstein-Uhlenbeck como uma modelagem do comportamento da musculatura adiposa que se estende em torno do valor médio. Embora o processo possa se desviar do valor médio por causa de flutuações aleatórias, o ângulo de tração da musculatura adiposa (semelhante ao regresso do valor médio) garante que ela finalmente retorne ao valor médio.

Comparação com outros processos aleatórios

Como o processo OU está intimamente relacionado com a modelagem de vários fenômenos financeiros, ele é frequentemente comparado a outros processos aleatórios, como o movimento Browniano e o movimento Browniano Geométrico (GBM). Ao contrário do movimento Browniano, o processo OU tem um comportamento de regresso ao valor médio, o que o torna mais adequado para a modelagem de cenários em que as variáveis giram em torno de um equilíbrio estável.

Em comparação com o GBM, normalmente usado para modelar o preço de uma ação e que inclui elementos de derivação e oscilação, o processo OU não apresenta crescimento exponencial, mas sim oscilação em torno de sua média. O GBM é mais adequado para modelar quantidades que crescem ao longo do tempo, enquanto o processo OU é mais adequado para modelar variáveis que exibem características de regressão da média.

Exemplos de finanças quânticas

O processo de Ornstein-Uhlenbec tem uma ampla aplicação no campo financeiro, especialmente em cenários de modelagem onde a regressão de valor médio é uma característica-chave. A seguir, discutiremos alguns dos casos de uso mais comuns.

Modelagem de taxas de juros

Uma das aplicações mais destacadas do processo OU é para a modelagem de taxas de juros, especialmente no quadro do modelo de Vasicek. O modelo de Vasicek assume que as taxas de juros seguem o processo OU, ou seja, as taxas de juros tendem a regressar à média de longo prazo ao longo do tempo. Esta característica é crucial para simular com precisão o comportamento das taxas de juros, pois as taxas de juros tendem a não flutuar indefinidamente, mas a flutuar perto de níveis médios influenciados pelas condições econômicas.

Preço dos ativos

No preço de ativos, especialmente em títulos de rendimento fixo, o processo OU é frequentemente usado para simular a evolução da taxa de retorno dos títulos. A natureza regressiva do valor médio do processo OU garante que a taxa de retorno não se desvie muito do seu valor médio histórico, o que está de acordo com o comportamento do mercado observado. Isso torna o processo OU uma ferramenta valiosa para o preço de títulos e outros instrumentos sensíveis à taxa de juros.

Estratégia de par de negociação

A parceria é uma estratégia de neutralidade de mercado que envolve a construção de posições de compensação em dois ativos relacionados. Nesse caso, o processo OU é especialmente útil, pois permite a modelagem da diferença de preço entre os dois ativos, que geralmente é a regressão ao valor médio. Ao usar o processo OU para modelar a diferença de preço, o comerciante pode confirmar os pontos de entrada e saída de lucro quando o preço se desvia do seu valor médio e prever a regressão ao valor médio, gerando assim um sinal de negociação.

Por exemplo, se a diferença de preço entre dois futuros se expande para além de um determinado limiar, o comerciante pode fazer um curto-circuito de um futuro de excelente desempenho e fazer mais de um futuro de mau desempenho, na expectativa de que a diferença de preço retorne ao seu nível médio histórico e, assim, obter lucro quando a reversão ocorre.

Solução do SDE de Ornstein-Uhlenbeck

A fórmula da equação diferencial do processo Ornstein-Uhlenbeck é a base da sua solução. Para a solução deste SDE, usamos o método de fator de integração. Vamos reescrever o SDE:

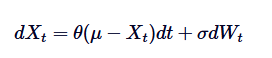
Primeiro, nós multiplicamos ambos os lados pelo fator de integração /upload/asset/28dfe9abfb54772651590.png:

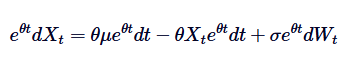
Observe que, se adicionarmos 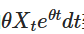em ambos os lados, a esquerda pode ser representada como a diferença do produto:

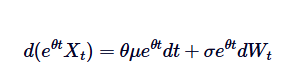
Assim, se nós integramos ambos os lados de 0 para t, temos:

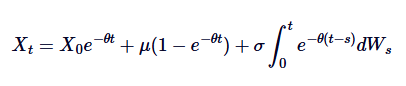
Esta é a definição geral do SDE Ornstein-Uhlenbeck.

A solução explícita deduzida acima tem vários significados importantes: o primeiro, /upload/asset/28e1d566f8ac15287edf3.png, indica que o valor inicial diminui com o tempo, indicando como o processo gradualmente esquece o seu ponto de partida. O segundo, /upload/asset/28df8a8a50df8d8362d7c.png, indica que o processo tende a uma média de μ-valores com o tempo. O terceiro, introduz a aleatoriedade, em que a integral do processo de Wiener explica a flutuação aleatória.

Esta solução enfatiza o equilíbrio entre o comportamento de regressão do valor médio da certeza e o parâmetro aleatório impulsionado pelo movimento de Brownian. A compreensão desta solução é fundamental para a simulação eficaz do processo OU, como descrito a seguir.

Ligações com outros processos aleatórios

O processo de Ornstein-Uhlenbeck tem várias ligações importantes com outros processos aleatórios famosos (incluindo o movimento de Brown e o modelo de Vasicek).

Relação com o movimento Brown

O processo de Ornstein-Uhlenbeck pode ser visto como uma versão regressiva do movimento browniano. O movimento browniano descreve um processo com tendência de aumento independente e sem regresso ao valor médio, enquanto o processo de OU introduz a regresso ao valor médio, usando um derivado de derivação para modificar o movimento browniano e, assim, puxar o processo para o valor central. Matematicamente falando, o processo de OU é simplificado para o movimento browniano padrão com um conjunto de ondulações:

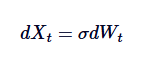
Assim, o movimento de Brown é um caso particular do processo OU, correspondendo à ausência de regressão à média.

Relação com o modelo Vasicek

O modelo de Vasicek é amplamente utilizado na modelagem de taxas de juros, sendo essencialmente uma aplicação do processo de Ornstein-Uhlenbeck na evolução das taxas de juros. O modelo de Vasicek assume que as taxas de juros seguem o processo OU, onde o SDE é definido como:

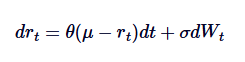
Dentre eles, rt representa a taxa de juros de curto prazo, a interpretação dos parâmetros θ, μ e δ é semelhante à interpretação do processo OU. A capacidade do modelo Vasicek de gerar um caminho de taxa de juros de retorno ao valor médio é uma de suas principais vantagens na modelagem financeira.

Compreender essas relações permite compreender mais amplamente como o processo OU é usado em diferentes contextos, especialmente no setor financeiro. Vamos explorar o significado prático dessas relações ao discutir exemplos de aplicação abaixo.

Simulação do processo Ornstein-Uhlenbeck usando Python

Nesta seção, vamos explorar como usar o Python para simular o processo Ornstein-Uhlenbeck (OU). Isso envolve o uso da dispersão de Euler-Maruyama para dispersão de equações de diferenciação aleatória que definem o processo OU (SDE).

Descentralização do SDE

Vamos rever as fórmulas matemáticas do SDE acima e dar um resumo de cada termo:

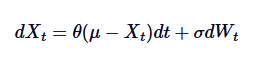
em,

• Xt é o valor do processo no tempo t.
• θ é a velocidade de regressão do valor médio.
• μ é a média de longo prazo do processo.
• δ é o parâmetro da taxa de flutuação .
• dWt representa o incremento do processo de Wiener (movimento padrão de Brown).

Para simular este processo no computador, precisamos de dispersão do SDE de tempo contínuo. Um método comum é a dispersão de Euler-Maruyama, que aproxima o processo contínuo levando em consideração o pequeno tempo de dispersão. A forma dispersão do processo de Ornstein-Uhlenbeck é dada pela seguinte fórmula:

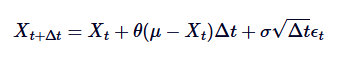
Dentre eles, 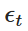é uma variável aleatória extraída da distribuição normal padrão (ou seja, 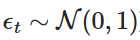). Esta dispersão permite que se compute o valor de Xt em uma sequência de tempo para simular o comportamento do processo OU.

Implementação Python

Agora, vamos implementar o processo Ornstein-Uhlenbeck descentralizado em Python.

Primeiro, importamos o NumPy e o Matplotlib de forma padrão. Em seguida, designamos todos os parâmetros para o modelo OU. Em seguida, pré-asignamos um array NumPy de comprimento N para adicioná-lo ao que foi calculado o caminho OU. Em seguida, iteramos N-1 (o passo 1 é a condição inicial X0 indicada), simulamos o incremento aleatório dW, e então computamos a próxima iterada do caminho OU de acordo com a fórmula matemática acima.

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 10.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

Os resultados são os seguintes:

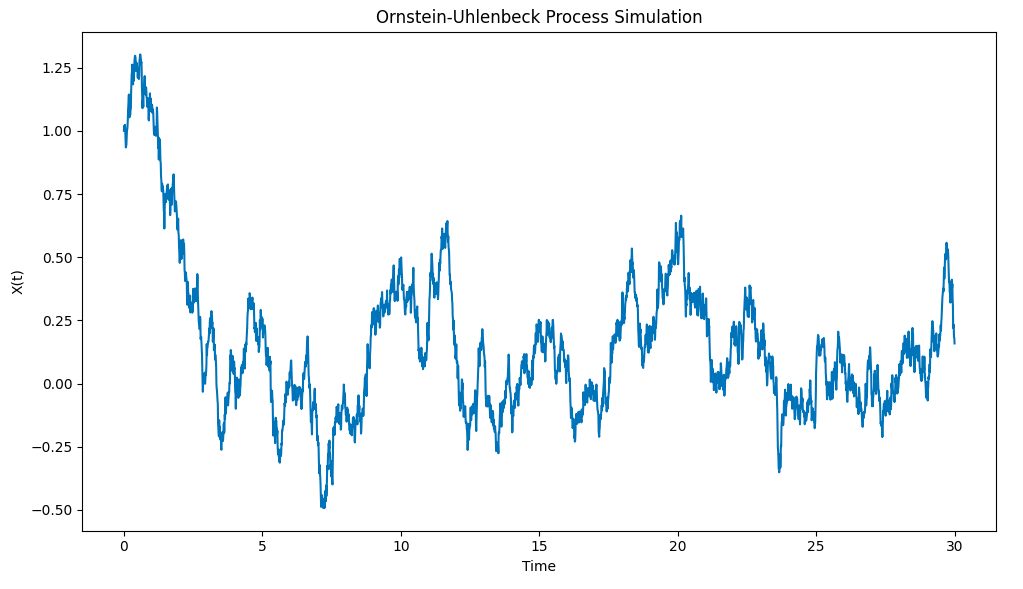
Simulação do processo Ornstein-Uhlenbeck desenhada em Python

Observe como o processo puxa rapidamente o átomo X0 = 1 para o valor médio μ = 0 a partir da condição inicial, e então, quando ele se desvia desse valor médio, ele mostra uma tendência para retornar a esse valor médio.

Resumo e seguimento

Neste artigo, descrevemos o processo Ornstein-Uhlenbeck, descrevemos suas fórmulas matemáticas e fornecemos uma implementação básica do Python para simular uma versão discreta do SDE de tempo contínuo. Em artigos subsequentes, examinaremos os SDE mais complexos construídos com base no processo OU e veremos como eles podem ser usados em aplicações de negociação de sistemas e de preços de derivativos.

Código completo

# OU process simulation

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 30.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

O artigo principal desta edição foi publicado em http://www.quantstart.com/articles/ornstein-uhlenbeck-simulation-with-python/