Fórmula de Kelly - uma ferramenta poderosa para controle de posição

** Suponha que o empate 1: a probabilidade de ganhar é de 60%, a probabilidade de perder é de 40%. A taxa de ganho líquido é de 100%, e a taxa de perda é de 100%. Isto é, se você ganhar, então você pode ganhar 1 dólar por cada dólar, se perder, então você perderá 1 dólar por cada dólar.

• Para este empate, o lucro esperado por cada aposta é de 60% do valor apostado.*1-40%*1=20%, o lucro esperado é positivo. Ou seja, é um empate em que os hackers têm uma vantagem muito grande.

  Então, como é que devemos apostar?

  Se não pensássemos rigorosamente, e imaginássemos de forma grosseira, acharíamos que, já que o lucro esperado de cada aposta é de 20%, para obter o máximo lucro a longo prazo, eu deveria colocar o maior número possível de partes do capital em cada aposta.

  Mas, obviamente, não é razoável que todos os jogos de azar coloquem 100% do capital, porque, se um jogo de azar for perdido, todos os fundos serão perdidos, não poderão participar do próximo jogo e só poderão sair do jogo. E, a longo prazo, o evento de perder uma vez é inevitável, portanto, a longo prazo, a falência é inevitável.

  Então, a conclusão é que, se houver uma chance de que um impasse leve a perda de todo o capital, mesmo que essa chance seja muito pequena, a posição nunca estará cheia.
  Porque, a longo prazo, eventos de pequena probabilidade inevitavelmente ocorrem, e na vida real, a probabilidade real de ocorrência de eventos de pequena probabilidade é muito maior do que a sua probabilidade teórica. É o efeito cola de saponina na finança.

• 2 Continuando com o impasse 1.
  Se apostar 100% de cada vez não é razoável, então o que acontece com 99%? Se apostar 99% de cada vez, não só é garantido que você nunca vai à falência, mas com sorte, você pode obter um grande lucro.

  E se a realidade for essa?

  Nós não analisamos o problema teoricamente, nós podemos fazer um experimento. Nós simulamos o impasse e apostamos 99% em cada vez para ver o que acontece.

  A simulação é muito simples e pode ser feita com o Excel. Veja o gráfico abaixo:

  
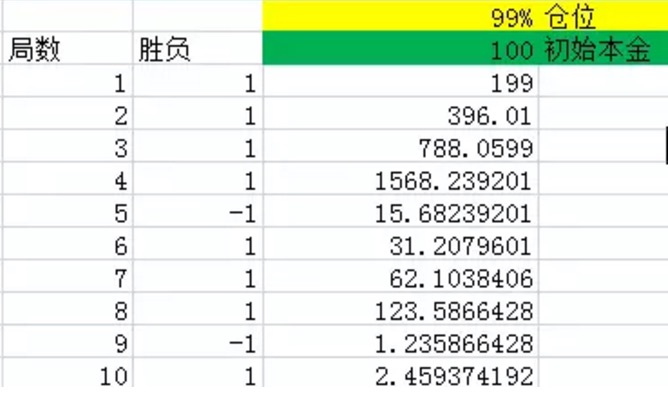  Gráfico 1

  Na figura acima, a primeira coluna representa o número de rodadas. A segunda coluna representa a vitória, e o Excel produzirá um 1 com 60% de probabilidade, ou seja, uma probabilidade de 60% de lucro líquido de 1,40% de probabilidade de gerar -1, ou seja, uma probabilidade de 40% de lucro líquido de -1. A terceira coluna representa o jogo de todos os fundos no final de cada rodada.

  Como você pode ver no gráfico, depois de 10 jogadas, a probabilidade de ganhar 8 jogadas em 10 jogadas é maior do que 60%, perdendo apenas duas vezes.

  Quando eu aumentava o número de experiências para 1000, 2000, 3000... o resultado era que, no final, o dinheiro em mãos era basicamente zero.

  Como 99% não funciona, vamos tentar outras proporções e veremos o seguinte gráfico:
  O gráfico mostra que, quando a posição é gradualmente reduzida, de 99%, para 90%, 80%, 70%, 60%, o resultado das mesmas 10 rodadas é completamente diferente. O gráfico parece mostrar que, à medida que a posição é gradualmente reduzida, o capital após 10 rodadas é gradualmente maior.

  Quando você olha para isto, percebe que o problema do empate não é tão simples.

  Então, como apostar para maximizar os lucros a longo prazo?

  Não deve ser, porque quando a proporção se torna zero, obviamente não há dinheiro a ser ganho.

  Então, qual é a melhor proporção?

  É o problema que a famosa fórmula de Kelly tem que resolver!

  
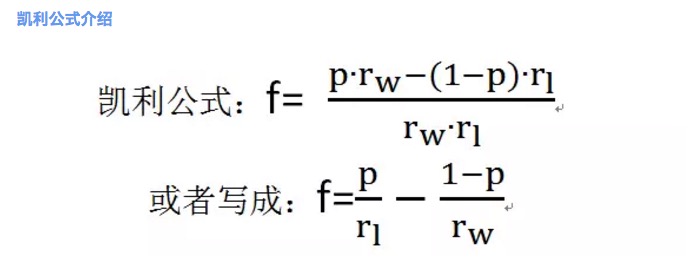  Gráfico 2

  Onde f é a proporção de apostas ideal; p é a probabilidade de ganhar; rw é a taxa de ganho líquido quando se ganha, por exemplo, rw = 1 em um jogo de azar; rl é a taxa de perda líquida quando se perde, por exemplo, rl = 1 em um jogo de azar; note que rl > 0 aqui.

  De acordo com a fórmula de Kelly, pode-se calcular que a percentagem de maior aposta no empate 1 é de 20%.

  Podemos fazer uma experiência para aprofundar a compreensão desta conclusão.

  
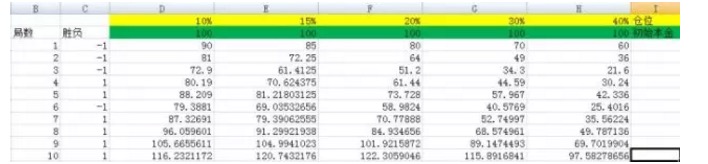  Gráfico 3

  Na figura, nós definimos posições de 10%, 15%, 20%, 30% e 40%, respectivamente. As colunas correspondentes são D, E, F, G e H.

  Quando eu fiz o experimento em 3000 vezes,
  Quando eu fiz o teste em 5000 vezes,
  A coluna F corresponde ao resultado maior, e a raiz de pressão em relação às outras colunas não é uma ordem de magnitude. A coluna F corresponde a uma proporção de posições de 20%.

  Veja o poder da fórmula de Kelly. No experimento acima, se você tiver a infelicidade de escolher a proporção de 40%, ou seja, a coluna H correspondente, depois de apostar 5.000 vezes, seu capital, embora tenha passado de 100 para 22799985.75, será um lucro enorme. Mas comparado com o resultado da proporção de 20%, isso é o equivalente a não ganhar dinheiro.

  Este é o poder do conhecimento!

• 3 Compreender a fórmula de Kelly

  A dedução matemática da equação de Kelly e sua complexidade requerem um conhecimento muito profundo de matemática, então não faz sentido discutir aqui. Aqui, vou aprofundar a compreensão subjetiva da equação de Kelly por meio de alguns experimentos.

  Vamos ver um empate: o empate 2: a probabilidade de você perder e ganhar é de 50%, por exemplo, jogar uma moeda. Quando você ganha, a taxa de ganho líquido é de 1, ou seja, rw = 1, e quando você perde, a taxa de perda líquida é de 0,5, ou seja, rl = 0,5. Ou seja, quando você ganha um dólar, você ganha outro dólar, quando você ganha, você só tem que pagar 5 cêntimos quando perde.

  É fácil ver que a expectativa de ganho para o impasse 2 é de 0,25, mais um impasse em que os hackers têm uma grande vantagem.

  De acordo com a fórmula de Kelly, a melhor proporção de apostas por jogo é:

  
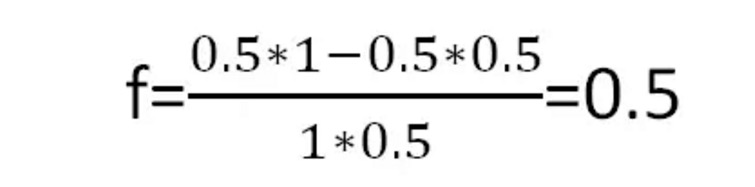  Gráfico 4

  O que significa que, a cada vez que você joga metade do seu dinheiro, você obtém o maior lucro a longo prazo.

  A seguir, eu vou criar um conceito de taxa de crescimento médio r baseado em experiências.

  Em primeiro lugar, vejamos os dois gráficos da experiência 2.1:

  
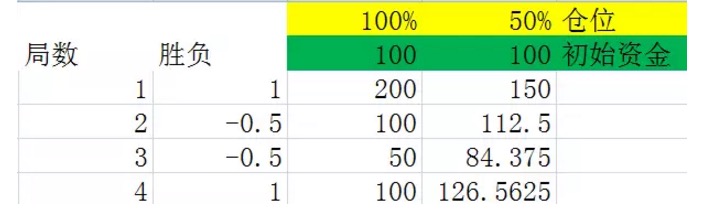  Gráfico 5

  Os dois gráficos são simulações de um empate 2 em que a probabilidade de um empate é de 50% na segunda coluna, resultando em 1 para um ganho de 100%. A probabilidade de um empate é de 50% para um ganho de -0.5 para um prejuízo de 50%. A terceira e quarta colunas são as posições de 100% e 50%, respectivamente, do capital que você possui após cada empate.

  Comparando cuidadosamente os dois gráficos, pode-se concluir que, após o mesmo número de partidas, o resultado final está relacionado apenas com o número de partidas vencidas e o número de partidas perdidas nesses números de partidas, e não com a ordem das partidas vencidas e perdidas nesses números de partidas. Por exemplo, nos dois gráficos anteriores, também foram realizadas 4 partidas, também em cada um dos gráficos houve duas vitórias e duas derrotas, mas a ordem perdida no primeiro gráfico foi vitória e derrota, e a ordem perdida no segundo gráfico foi vitória e derrota.

  É claro que essa conclusão é muito fácil de provar (a lei da troca de multiplicação, os alunos do ensino básico), mas não é uma prova, os dois exemplos acima são suficientes para que todos entendam bem.

  Então, já que o resultado final não tem a ver com a ordem de ganhos e perdas, vamos supor que o empate 2 ocorreu da mesma forma que o experimento 2.2.

  
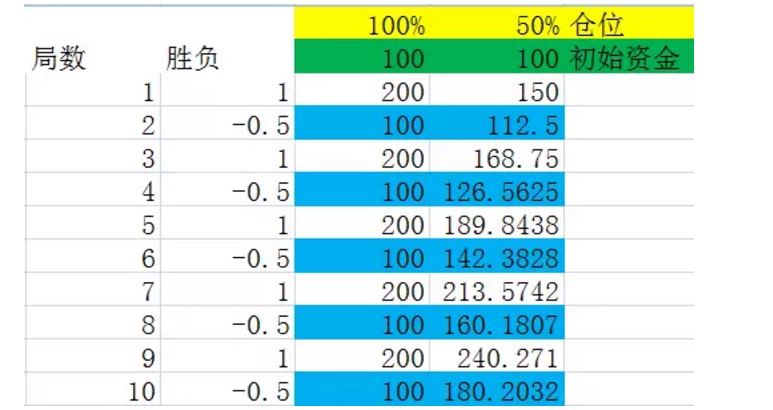  Gráfico 6

  Suponhamos que o empate tenha sido um empate alternado, pois a conclusão é que, a longo prazo, o dinheiro não tem qualquer influência sobre o resultado.

  Antes de observarmos o quadro, devemos fazer uma definição. Suponha que consideremos um conjunto de loterias como um todo, no qual a frequência de resultados é exatamente igual à sua probabilidade, e o número de loterias desse conjunto é o menor número de loterias em todo o conjunto de condições. Por exemplo, no experimento acima, um conjunto de loterias representa uma loteria de duas loterias, em que cada um ganha e perde.

  Observe atentamente os números marcados em azul no gráfico acima, eles são o final de um conjunto de paradas. Você verá que esses números são de crescimento estável. Quando a posição é de 100%, a taxa de crescimento dos números marcados em azul é de 0%, ou seja, a taxa de crescimento do capital após um conjunto de paradas é de 0%. Isso também explica que, quando todas as posições estão cheias, não é possível ganhar dinheiro a longo prazo no jogo 2. Quando a posição é de 50% (ou seja, a melhor proporção obtida pela fórmula de Kelly), a taxa de crescimento dos números marcados em azul é de 12,5%, ou seja, a taxa de crescimento do capital após um conjunto de paradas é de 12,5%

  É uma regra geral que a taxa de crescimento após cada paralisação está relacionada com a posição. E quanto maior a taxa de crescimento após cada paralisação, maior o lucro final a longo prazo.

  A taxa média de crescimento de cada paralisação pode ser calculada de acordo com a taxa de crescimento de cada paralisação g. Na figura acima, se cada paralisação contém duas paralisações, então a taxa média de crescimento de cada paralisação

  
  Gráfico 7

  Em termos de longo prazo, para que o capital obtenha o maior crescimento, é preciso maximizar r, ou seja, maximizar g. A melhor proporção de aposta f é, na verdade, obtida pela solução de max (g).

• 4. Outras conclusões da fórmula de Kelly sobre o risco

A lenda de Kelly

A fórmula de Kelly foi originalmente criada para o físico John Larry Kelly, da AT&T Bell Labs, com base em pesquisas de seu colega Claude Elwood Shannon sobre mensagens de longa distância. Kelly resolveu a questão de como a teoria da informação de Shannon deve ser aplicada a um jogador que possui informações internas no jogo. O jogador deseja decidir o melhor valor de aposta, e suas informações internas não precisam ser perfeitas (sem mensagens), o que lhe dá uma vantagem útil.
Thorpe usou o seu tempo de trabalho para escrever um artigo matemático sobre o jogo de 21 pontos, depois de meses de cálculos difíceis. Ele usou seu conhecimento para invadir todos os cassinos da cidade de Reno, Nevada, durante a noite, e conseguiu ganhar dezenas de milhares de dólares com a mesa de 21 pontos. Ele também foi o antepassado do hedge fund de negociação quantitativa de Wall Street, criando o primeiro hedge fund de negociação quantitativa nos anos 70.

Usando Perspectivas

Como usar a fórmula de Kelly para ganhar dinheiro na vida real?
O que é preciso é criar um impasse que satisfaça as condições de aplicação da fórmula de Kelly.
Recentemente, eu estive fazendo uma pesquisa sobre sistemas de negociação, e o que é mais importante para um bom sistema de negociação? Uma regra de compra e venda com expectativa de lucro positivo é 10% da importância, enquanto um bom método de controle de fundos é 40% da importância, e o restante 50% é o controle psicológico das pessoas.
E a fórmula de Kelly é a ferramenta que me ajuda a controlar as minhas posições financeiras.
Por exemplo, um sistema de negociação de ações que eu pesquisei anteriormente, o sistema realiza uma negociação por semana, a probabilidade de sucesso de negociação por semana é de 0,8, a probabilidade de fracasso é de 0,2%. Quando o sucesso pode ganhar 3% ((dedução de comissões, imposto de estampagem), a perda de 5% em cada falha. Antes de saber a fórmula de Kelly, eu era um negociador cego, e não sabia que a minha posição estava errada.
É claro que a fórmula de Kelly não pode ser tão simples na aplicação prática, e há muitas dificuldades a serem superadas. Por exemplo, o custo de capital necessário para as bolsas de levadura, por exemplo, o capital na realidade não é infinitamente divisível, por exemplo, no mercado financeiro não é tão simples quanto a simples paralisação mencionada acima.
Mas, de qualquer forma, a fórmula de Kelly nos mostra o caminho a seguir.