Matemática e jogo

• Sabemos que o jogo de azar é um jogo de probabilidade, e foi por causa de alguns resultados estranhos que o jogo despertou o interesse do matemático Pascal e do grande matemático Fermat, que, através de uma correspondência, propuseram alguns princípios da teoria da probabilidade, criando a teoria da probabilidade. Hoje, a matemática vai apresentar alguns tópicos de probabilidade em jogos de azar, para que todos saibam que, para jogar, é preciso fazer um cálculo minucioso.

• 1. O jogo perfeito

Há um jogo entre os Lakers e os Cowboys da NBA, e os dois times têm fãs leais, por isso, chame-os de Coyotes e Cowboys. Os fãs, claro, acham que o time que apoiam tem mais probabilidade de ganhar, por isso apostam com você. Suponha que os Coyotes acham que os Lakers têm probabilidade de ganhar p, e os Cowboys acham que os Cowboys têm probabilidade de ganhar q, p e q.

O método é o seguinte: nós jogamos o mesmo jogo que o jogo da raça Sphynx e o jogo da raça Sphynx, e se ganharmos ganhamos y e se perdermos perdemos x, desde que y > x. E x e y apenas precisam satisfazer as seguintes duas inequações simples, e a expectativa de ganho da raça Sphynx e a raça Sphynx é positiva, então nós apostamos:

            
            
            
```
p * x - ( 1-p ) * y > 0
q * x - ( 1-q ) * y > 0
```

Além da restrição de y > x, a imagem desenhada é a área circundada por três linhas retas, para o valor de coordenadas de qualquer ponto no interior ((x, y) é um solução vencedora. Se p > q, a solução é a parte azul do gráfico a seguir:

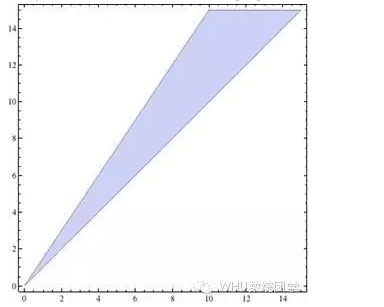
A questão parece ter sido resolvida perfeitamente, mas há uma dúvida que, creio, o leitor descobrirá em breve como é absurda: quer sejam os macacos-humanos ou os macacos-macacos-vaqueiros, os lucros esperados são positivos, ou seja, eles ganham dinheiro a longo prazo, enquanto nós estamos em apuros, de onde vem todo esse dinheiro e como é possível que todo mundo ganhe dinheiro?

• O truque dos dois ou três cartões.

  

Este é outro truque inteligente. Começamos com três cartas: a primeira é preta do lado oposto, a segunda é vermelha do lado oposto, a terceira é preta do lado oposto, a terceira é vermelha do lado oposto. Depois, colocamos as cartas em uma caixa, sacudimos as cartas e deixamos o oponente tirar uma carta plana e colocá-la na mesa.

Na verdade, a nossa probabilidade de ganhar não é 1/2, mas sim 2/3, e o que mais nos confunde neste jogo é a dupla face dos cartões. O jogador não tem três faces, mas sim seis: três faces pretas e três faces vermelhas. Nós numeramos as seis faces A, B, C, D, E, F:

Quando o jogador tira a face preta, são as três possibilidades A, C, D, e suas faces traseiras são D, F e A, respectivamente, com a face preta ocupando 2/3 da posição.

O problema foi proposto em 1889 pelo matemático francês Joseph Louis François Bertrand, e foi chamado de paradoxo da caixa de Bertrand por causa de um resultado inesperado. Em 1950, o matemático americano Warren Weaver introduziu o jogo de cartas acima, que Martin Gardner chamou de fraude de três cartas.

• 3 - Uma Cereja tão Extraordinária

  

  Às vezes, quando começamos a jogar, deixamos que os outros ganhem um pouco de dinheiro, lançamos uma longa linha para pescar um peixe grande e, finalmente, acabamos com a rede. Abaixo está um excelente exemplo. Quatro pessoas estão jogando bridge, e eu primeiro digo: venha jogar um jogo de craps, eu agora tenho um A, e você adivinha se eu tenho mais A?

  Muitas pessoas acham que não há nenhuma diferença entre duas maçãs, e que não importa adicionar uma maçã. Mas a diferença entre elas é inacreditável. Vamos calcular a probabilidade da primeira maçã:

  
              
              
              
  没有A的情形：C（48，13）
  至少有1张A的情形：C（52，13）－C（48，13）
  恰好有1张A的情形：4＊C（48，12）
  至少有2张A的情形：C（52，13）－C（48，13）－4＊C（48，12）
  事件X为至少有两张A，事件Y为至少有一张A，那么条件概率为：
  
  P（X｜Y）＝P（XY）／P（Y）=(C（52，13）－C（48，13）－4＊C（48，12）)/(C（52，13）－C（48，13）)≈37%
  

  Agora eu tenho que ganhar e A, é mais fácil de perder. Mas depois de ter o primeiro jogo, a vontade de apostar todos foram mobilizados, um olhar para o segundo jogo não é apenas mudar de roupas, todos aumentaram a aposta, em seguida, eu não tenho mais A, no meio de nós. A probabilidade do segundo jogo é muito diferente:

  
              
              
              
  有黑桃A的情形：C（51，12）
  没有其它A的情形：C（48，12）
  还有其它A的情形：C（51，12）－C（48，12）
  事件X为还有其它A，事件Y为有黑桃A，条件概率为：
  
  P（X｜Y）＝P（XY）／P（Y）＝（C（51，12）－C（48，12））／C（51，12）≈56%。
  

Reprodução de WHU Numerology