Perseguindo Garotas e Encontrando Mísseis - Estatísticas da Fórmula Bayesiana

• ### ONE

Os meta-racionalistas que não entendem o humor inevitavelmente terão um momento de tristeza na vida emocional: encontrar uma garota bonita por acaso, pensar dia e noite, perder o sono e comer, começar uma longa viagem de amor secreto, esperar até que um dia, em confusão interminável, finalmente reunir a coragem de confessar a garota, o resultado é que a garota diz que eu já tenho um namorado que é tão feliz quanto o diabo, é difícil de aceitar …

Para evitar esse tipo de constrangimento, como determinar com precisão se uma garota é solteira ou não é um curso obrigatório.

Se você trabalha com uma garota, muitas vezes ao lado dela, saber se ela é solteira não é um problema difícil. Mas a tarefa de alta dificuldade que os mortais precisam realizar é: como um estranho que mantém distância da garota, sem a percepção da garota, você pode determinar a situação de solteiro da garota com informações limitadas em mãos.

O primeiro passo é acreditar na intuição. Os racionalistas podem considerar encontrar mais amigos para observar secretamente a garota-alvo. Claro que não todos os que procuram devem ser racionalistas. Qualquer grupo de identificação de problemas mentais, esmagador de rumores, controle natural, médico forense criminalista é melhor encontrar alguns. Os casados, os veteranos do cenário, os ladrões de flores também devem encontrar, quanto mais melhor, melhor e mais diversificado.

Para isso, devemos dar o segundo passo, falar com fatos e evidências: um homem é solteiro ou não, e a resposta pode ser encontrada em muitos detalhes.

Assim como fazer uma pesquisa científica, você pode pesquisar os dados, e uma pesquisa casual no Google pode encontrar critérios simples e fáceis de usar para identificar solteiros que muitos solitários pesquisaram por anos, como o princípio do telefone celular, o princípio do auto-aprendizagem, as meninas solteiras costumam fazer auto-aprendizagem com algumas meninas. Depois, faça uma pesquisa estatística sobre se as meninas solteiras já sabem ou não, é claro, quanto maior o espécime, melhor.

E outras estatísticas.

Quando esses dados de experimentação de ratos estiverem disponíveis, podemos continuar e corrigir e otimizar o valor de probabilidade de 65,65% que acabou de ser votado. Dependendo do que? Naturalmente, o desempenho da garota-alvo em vários critérios. Por exemplo, descobrir que o MM alvo gosta de se exercitar com amigos, e de acordo com os resultados da pesquisa de estatística de ratos: entre os MM que já estão apaixonados, as meninas que gostam de se exercitar com amigos representam cerca de 60%; entre as meninas que não estão apaixonadas, as meninas que gostam de se exercitar com amigos representam cerca de 30%;

Então agora a probabilidade de que o alvo é mm é solteiro vai se transformar em

A morte é uma festa, mas a esperança é maior!

Se os resultados do estudo também revelarem que a taxa de uso de celulares é superior a 1,2 vezes por hora em meninas solteiras, o que representa 20%; entre as meninas que já estão no amor, esse valor é de 60%.

A probabilidade de solteirismo foi tragicamente reduzida para 56,02%, mas os meta-racionalistas podem procurar mais critérios de avaliação de opinião, fazer mais pesquisas, atualizar o valor da probabilidade de solteirismo das meninas, para que ele fique cada vez mais próximo da verdade, mas antes de obter o resultado final, você deve estabelecer um limite: a probabilidade de solteirismo das meninas é superior a esse limite (por exemplo, 90%), você deve ser digno de confessar, ou então, seja morto.

No entanto, é importante notar que, independentemente do número de vezes que o cálculo é feito, o resultado é um valor de probabilidade, não é um fato, mesmo depois de vários estudos, já é possível determinar a probabilidade de solteirona da garota-alvo para 99.9%, imediatamente pronto para confessá-la, mas no último estudo de observação da garota, descobriu-se que as pessoas e um homem se dão as mãos e dizem rir e abraçarem-se, então, a probabilidade de solteirona da garota cairá imediatamente de 99.9% para perto de 0, o resultado é compreensível …

Este artigo mostra que este método rigoroso e racional de julgar se um homem é solteiro é conhecido como método estatístico de Bayes. O método de Bayes é simplesmente o seguinte: a probabilidade antecipada + a nova evidência = a probabilidade correta.

Mas, de qualquer forma, a teoria de Bayes, inventada pelos mortais, não pode ser ignorada. A Marinha dos EUA usou esse método para procurar bombas de hidrogênio perdidas e submarinos nucleares desaparecidos no Oceano Pacífico, e agora vamos passar do canal emocional para o canal histórico.

• ### TWO

Um dia de janeiro de 1966, um bombardeiro B-52 norte-americano voou sobre Palomarés, na Espanha, com vários pilotos a bordo do avião executando uma missão de reabastecimento aéreo organizada pelo Comando da Força Aérea. O piloto era um homem tranquilo, que não gostava de pegar um grande tubo de gasolina, mesmo na cabine do avião.

Mas a história ainda não acabou, e uma série de tragédias e comédias se seguiram.

Para encontrar a bomba de hidrogênio perdida, os Estados Unidos mobilizaram uma força de busca interna com vários especialistas, incluindo um matemático chamado John Craven, o principal cientista do Departamento de Programas Especiais da Marinha dos Estados Unidos.

Em busca de uma bomba de hidrogênio, o programa proposto por Craven usa o método Bayesian já mencionado, ele convoca especialistas de todos os âmbitos, mas cada especialista tem sua própria área de especialização, e não é universal. Alguns sabem muito sobre o B-52, mas pouco sobre as características da bomba de hidrogênio.

Para responder a esta variedade de questões, Craven pediu aos especialistas que fizessem várias hipóteses, imaginando vários cenários e, em seguida, adivinhando a probabilidade de uma bomba de hidrogênio estar em cada um deles e a probabilidade de ocorrência de cada situação.

O método de Craven também foi questionado por seus colegas, porque em seu programa, muitos dos resultados foram obtidos por esses especialistas em forma de conjecturas, votos e até mesmo jogos de azar, não sendo possível garantir a precisão de todos os resultados, mas, como a missão de procurar bombas de hidrogênio era urgente e não havia tempo para realizar experimentos precisos e estabelecer uma teoria confiável e completa, o método de Craven era uma solução viável.

Depois de obter os resultados de um concurso de prostituição de um especialista, Craven reuniu-os e desenhou um mapa de probabilidade do local da bomba atômica: dividiu toda a área possível em muitos quadrados pequenos, cada um com um valor de probabilidade diferente, com altos e baixos, como as linhas de altura equivalentes de montanhas e vales no mapa. Como os racionalistas para determinar se uma garota é solteira, Craven completou o primeiro passo do método de Bayes.

Depois disso, Craven e o comandante da Força de Busca começaram a procurar por uma bomba de hidrogênio, atualizando simultaneamente as probabilidades de cada grelha no decorrer da busca. No entanto, a localização indicada pela grelha com maior probabilidade é frequentemente um desfiladeiro e uma área de mar profundo em terra, e mesmo que a bomba de hidrogênio esteja realmente lá, ela não pode ser encontrada, então é necessário desenhar outro mapa de probabilidade que mostre que a bomba de hidrogênio já está lá e que a probabilidade de encontrar a bomba de hidrogênio é menor do que a probabilidade de encontrar a bomba de hidrogênio.

Apenas dois anos depois, em 1968, Craven teve a oportunidade de mostrar seu talento novamente, perdendo uma pequena munição de alumínio, desta vez para a Marinha dos EUA.

Em junho de 1968, o submarino nuclear Swan da Marinha desapareceu no Atlântico, no mar da Ásia, e todos os 99 oficiais da Marinha que estavam no submarino e no navio ficaram sem sinal. De acordo com o relatório de investigação posterior, o culpado foi uma estranha torreta no submarino, que foi lançada e, depois de ser atacada, virou-se para si mesma, fazendo com que a bala do submarino explodisse.

A Marinha dos Estados Unidos realizou uma busca em grande escala para encontrar o Swan, com a participação de Craven. Devido à velocidade lenta do submarino na hora do acidente, a direção e a magnitude do impacto da explosão, a direção do pára-quedas do submarino na hora da explosão são desconhecidas, mesmo sabendo onde o submarino explodiu, é difícil determinar onde os destroços do submarino acabaram sendo inundados.

Nenhum especialista pode estimar com precisão o que aconteceu com o submarino antes e depois do incidente, e, como na busca por bombas de hidrogênio, Craven consultou matemáticos, especialistas em submarinos e especialistas em resgate marítimo em várias áreas, e escreveu um roteiro de possíveis fraudes para que eles, com base em seu conhecimento e experiência, adivinhassem em que direção a situação se desenvolveria. Diz-se que, para dar um pouco de diversão ao trabalho árduo, Craven também preparou uma garrafa de uísque como prêmio para apostar no correto.

Finalmente, Craven recebeu um mapa de probabilidade de 20 milhas de mar. A área foi dividida em várias grades, cada uma com dois valores de probabilidade, p e q, onde p é a probabilidade de um submarino estar no grid, e q é a probabilidade de ser encontrado se o submarino estiver no grid. Segundo a experiência, o segundo valor de probabilidade está relacionado principalmente à profundidade do mar, e é mais provável que um submarino que falhou em uma busca em águas profundas perca a rede.

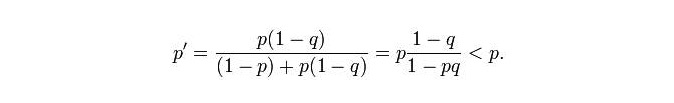
A probabilidade de existência de submarinos em outras grades aumenta:

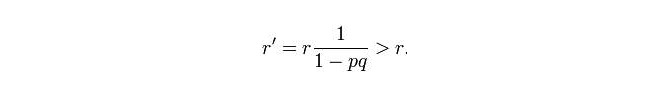
Cada busca seleciona uma das grades de maior probabilidade de ocorrência de submarinos em toda a região. Se não for encontrada, a distribuição de probabilidade será limpa uma vez, e os navios de busca irão para a nova grade mais suspeita para pesquisar, e assim por diante, até encontrar os cisnes.

Inicialmente, os oficiais da Marinha, com base na experiência, estimaram que o submarino estava no fundo do mar a leste do ponto da explosão, ignorando as recomendações de Craven e outros matemáticos, mas após meses de buscas, nada foi obtido. Mais tarde, a Marinha teve que seguir a recomendação de Craven, que, de acordo com o gráfico de probabilidade, o submarino após o acidente deveria estar no lado oeste do ponto da explosão. Após várias buscas, o submarino foi encontrado no fundo do mar a sudoeste do ponto da explosão.

Depois de duas demonstrações de força, o método de Bayes usado por Craven na pesquisa marítima tornou-se amplamente aceito, e desde então, o método de Bayes tornou-se uma palavra-chave que surgiu de forma inesperada e frequente, juntamente com bombas de hidrogênio e submarinos nucleares. Durante décadas, o método de Bayes foi cada vez mais amplamente aplicado, desde o filtro de pesquisa do Google até o conjunto de carros sem motorista para determinar sua posição de condução, penetrou em todos os cantos.

Reprodução de Modelagem Matemática de Anil