Sete técnicas de regressão que você deve dominar

**Este artigo explica a análise de regressão e seus benefícios, resumindo os sete tipos de regressão mais usados e seus elementos-chave, como regressão linear, regressão lógica, regressão polinomial, regressão gradual, regressão em cascata, regressão em cascata e regressão ElasticNet, e, finalmente, os elementos-chave para escolher o modelo de regressão correto. ** ** A análise de regressão de botão de codificador é uma ferramenta importante para a modelagem e análise de dados. Este artigo explica o significado da análise de regressão e suas vantagens, concentrando-se em resumir as sete técnicas de regressão mais usadas e seus elementos-chave, tais como regressão linear, regressão lógica, regressão multipolar, regressão gradual, regressão de arco, regressão de encaixe e regressão de ElasticNet, e, finalmente, os elementos-chave para escolher o modelo de regressão correto.**

• ### O que é a regressão?

A análise de regressão é uma técnica de modelagem preditiva que estuda a relação entre a variável causativa (objetivo) e a variável automática (previsor). Esta técnica é geralmente usada em análises preditivas, modelos de sequência temporal e relações causais entre variáveis encontradas. Por exemplo, a melhor maneira de estudar a relação entre a condução imprudente de motoristas e o número de acidentes de trânsito é a regressão.

A análise de regressão é uma ferramenta importante para a modelagem e análise de dados. Aqui, usamos curvas/linhas para encaixar esses pontos de dados, desta forma, a diferença de distância entre a curva ou a linha e o ponto de dados é mínima.

• ### Por que usamos a análise de regressão?

Como mencionado acima, a análise de regressão estima a relação entre duas ou mais variáveis. Vejamos um exemplo simples para compreendê-la:

Por exemplo, se você quiser estimar o crescimento das vendas de uma empresa em condições econômicas atuais. Agora, você tem os dados mais recentes da empresa, que mostram que o crescimento das vendas é cerca de 2,5 vezes o crescimento econômico. Então, usando a análise de regressão, podemos prever as vendas futuras da empresa com base em informações atuais e passadas.

Os benefícios da análise de regressão são muitos:

Ele mostra uma relação significativa entre a variável automática e a variável causativa;

Indica a intensidade do impacto de várias variáveis de origem sobre uma variável causadora.

A análise de regressão também nos permite comparar a interação entre as variáveis que medem diferentes escalas, como a relação entre a mudança de preço e o número de atividades promocionais. Isso é útil para ajudar os pesquisadores de mercado, analistas de dados e cientistas de dados a excluir e estimar o melhor conjunto de variáveis para a construção de modelos de previsão.

• ### Quantas tecnologias de regressão temos?

Há uma variedade de técnicas de regressão para a previsão. Estas técnicas têm três dimensões principais: o número de unidades de variação automática, o tipo de variação automática e a forma da linha de regressão. Vamos discutir detalhadamente essas técnicas na seção a seguir.

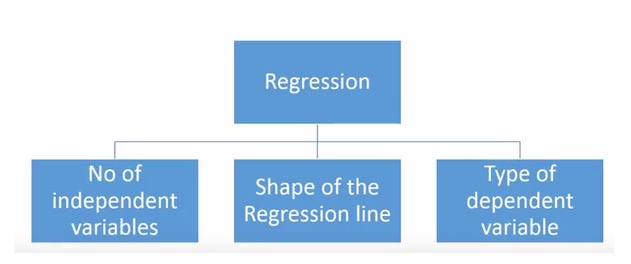
Para aqueles que são criativos, você pode até mesmo criar um modelo de regressão que não tenha sido usado, se achar necessário usar uma combinação desses parâmetros acima. Mas antes de começar, conheça os métodos de regressão mais usados:

• 1. Regressão Linear

  É uma das técnicas de modelagem mais conhecidas. A regressão linear é geralmente uma das técnicas preferidas para aprender modelos de previsão. Nessa técnica, a regressão linear é linear, uma vez que as variáveis são contínuas e as variáveis automáticas podem ser contínuas ou dissociadas.

  A regressão linear usa a linha de regressão de melhor adequação (ou seja, a linha de regressão) para estabelecer uma relação entre a variável de causalidade (ou seja, a variável Y) e uma ou mais autovariaveis (ou seja, a variável X).

  E eu vou escrever uma equação para isso, e eu vou escrever uma equação para isso.*X + e, onde a representa a interseção, b representa a inclinação da linha reta e e é o erro. Esta equação pode ser usada para prever o valor da variável alvo com base na variável de previsão dada (s).

  

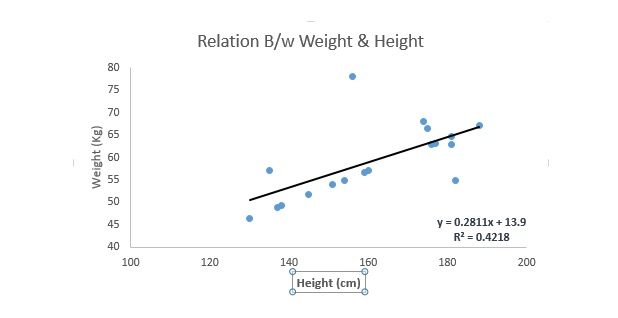
  A diferença entre a regressão unilinear e a regressão multilinear é que a regressão multilinear tem (< 1) uma variável automática, enquanto a regressão unilinear geralmente tem apenas uma variável automática. A questão agora é como obter uma melhor linha de encaixe?

  Como obter os valores da linha de melhor ajustamento (a e b)?

  Este problema pode ser facilmente resolvido com o método de minimizar o quadrado. O método de minimizar o quadrado é também o método mais usado para a simulação de regressão. Para dados de observação, ele calcula a melhor linha de simulação minimizando a soma do quadrado do desvio vertical de cada ponto de dados para a linha.

  

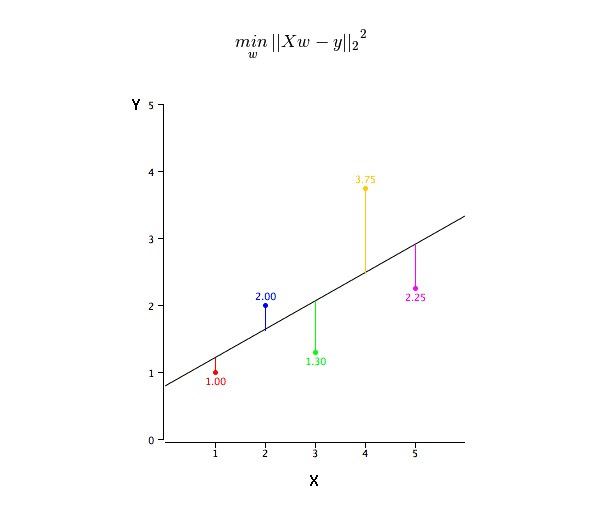
  Podemos usar os indicadores R-square para avaliar o desempenho do modelo. Para obter mais informações sobre esses indicadores, leia: Indicadores de desempenho do modelo Part 1, Part 2 .

  A questão é:

  • Deve haver uma relação linear entre a variável automática e a variável causativa
  • A regressão múltipla possui múltipla conilinearidade, autocorrelação e heterogeneidade.
  • A regressão linear é muito sensível a anomalias. Ela pode afetar gravemente a linha de regressão e, eventualmente, afetar os valores de previsão.
  • A convexidade múltipla aumenta a diferença entre as estimativas dos coeficientes, o que torna as estimativas muito sensíveis a pequenas variações no modelo. O resultado é que as estimativas dos coeficientes são instáveis.
  • No caso de várias auto-variáveis, podemos usar o método de seleção para a frente, o método de eliminação para trás e o método de seleção progressiva para escolher a auto-variável mais importante.

• 2. Regressão Logística

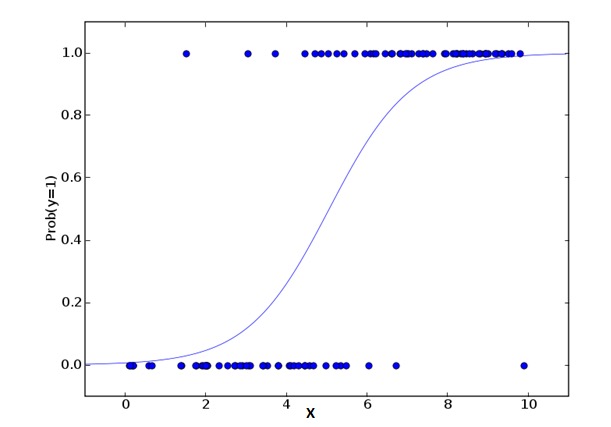
  A regressão lógica é usada para calcular a probabilidade de que um evento seja Success e um evento seja Failure. Quando o tipo de variável é binário ((¹⁄₀, verdadeiro/falso, sim/não) devemos usar a regressão lógica. Aqui, o valor de Y é de 0 a 1, que pode ser representado pela seguinte equação:

  odds= p/ (1-p) = probability of event occurrence / probability of not event occurrence
  ln(odds) = ln(p/(1-p))
  logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3....+bkXk
  

  Na fórmula acima, p representa a probabilidade de ter alguma característica. Você deve estar perguntando a seguinte pergunta: Por que usar logaritmos na fórmula?

  Uma vez que estamos usando uma distribuição binária ((de variáveis), precisamos escolher uma função de ligação que seja a melhor para essa distribuição. É a função Logit. Na equação acima, os parâmetros são escolhidos por meio da observação do valor da probabilidade máxima da amostra, em vez de minimizar o quadrado e o erro (como é usado na regressão normal).

  

  A questão é:

  • É amplamente utilizado para classificação.
  • A regressão lógica não requer que a relação entre a variável automática e a variável causativa seja linear. Ela pode lidar com vários tipos de relações, pois usa uma conversão de log não linear para o índice de risco relativo OR da previsão.
  • A fim de evitar sobreajustes e desajustes, devemos incluir todas as variáveis importantes. Há uma boa maneira de garantir que isso aconteça, usando o método de triagem gradual para estimar a regressão lógica.
  • É necessário um grande número de amostras, pois, em casos de menor número de amostras, a grande probabilidade de estimar o efeito é pior do que o mínimo quadruplo ordinário.
  • As variáveis próprias não devem estar inter-relacionadas, ou seja, não possuem múltipla conlinearidade. No entanto, na análise e modelagem, podemos optar por incluir a interação de variáveis de classificação.
  • Se o valor da variável de função for uma variável de ordem, ela é chamada de regressão lógica de ordem.
  • Se a função é multivariável, ela é chamada de regressão lógica múltipla.

• 3. Regressão polinomial

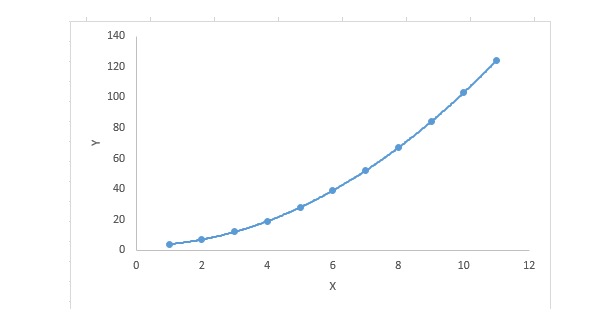
  Para uma equação de regressão, se o índice da variável é maior que 1, então ela é uma equação de regressão polinomial. A equação é a seguinte:

  y=a+b*x^2
  

  Nessa regressão, a linha de melhor encaixe não é uma linha reta, mas sim uma curva usada para encaixar pontos de dados.

  

  Os principais pontos:

  • Apesar de haver uma indução que permite a adequação de um polinomial de grau elevado e obter um erro mais baixo, isso pode levar a uma sobreadequação. Você precisa desenhar regularmente um gráfico de relacionamento para ver se a adequação está ocorrendo e se concentrar em garantir que a adequação seja razoável, sem sobreadequação nem falta de adequação.

  

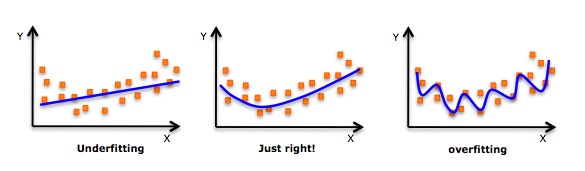
  • Obviamente, procure os pontos de curva em ambos os lados para ver se essas formas e tendências fazem sentido. Polinomios de grau mais alto podem acabar produzindo resultados inferenciais estranhos.

• 4. Regressão em etapas

  Podemos usar esta forma de regressão quando tratamos de múltiplas autovariaveis. Nessa técnica, a seleção das autovariaveis é feita em um processo automático, que inclui operações não-humanas.

  Este feito é feito observando valores estatísticos, como o R-square, t-stats e o indicador AIC, para identificar variáveis importantes. A regressão gradual se encaixa no modelo adicionando/excluindo simultaneamente as variáveis de co-regressão baseadas em padrões especificados.

  • A regressão gradual padrão faz duas coisas: adiciona e subtrai as previsões necessárias para cada passo.
  • A seleção avançada começa com as previsões mais significativas do modelo e adiciona variáveis a cada passo.
  • O método de eliminação de retrogradação começa ao mesmo tempo que todas as previsões do modelo, e depois elimina as variáveis menos significativas em cada etapa.
  • O objetivo dessa técnica de modelagem é maximizar a capacidade de previsão usando o menor número possível de variáveis de previsão. Esta é uma das maneiras de lidar com conjuntos de dados de alta dimensão.

• 5. Regressão de Ridge

  Análise de regressão de eixo é uma técnica usada para dados com múltiplos coeficientes de correlação entre variáveis. Em casos de múltiplos coeficientes de correlação entre variáveis, apesar de que o método de duplicação mínima (OLS) é justo para cada variável, as diferenças entre eles são tão grandes que os valores de observação são desviados e distantes do valor real. A regressão de eixo reduz o erro padrão adicionando um desvio à estimativa de regressão.

  Na parte de cima, vimos a equação de regressão linear.

  y=a+ b*x
  

  Esta equação também tem um elemento de erro. A equação completa é:

  y=a+b*x+e (error term),  [error term is the value needed to correct for a prediction error between the observed and predicted value]
  => y=a+y= a+ b1x1+ b2x2+....+e, for multiple independent variables.
  

  Em uma equação linear, o erro de previsão pode ser dividido em duas subcomponentes. Uma é a diferença e a outra é a divergência. O erro de previsão pode ser causado por essas duas proporções ou por qualquer uma delas.

  A regressão alveolar resolve o problema de covalência múltipla através do parâmetro de contração λ ((lambda)). Veja a fórmula abaixo

  

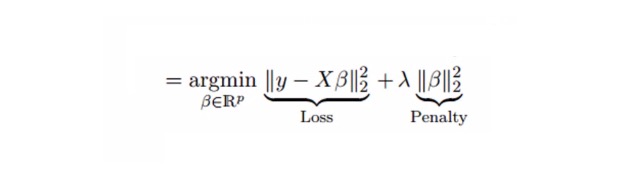
  Nessa fórmula, há duas componentes. A primeira é o mínimo quadruplo, e a outra é o múltiplo de λ de β2 (β-quadrado), onde β é o coeficiente relevante. Adicione-o ao mínimo quadruplo para obter um diferencial muito baixo para reduzir o parâmetro.

  A questão é:

  • A menos que seja um número constante, essa regressão é assumida de forma semelhante à regressão de menor quadruplo.
  • Ele reduziu o valor do coeficiente relevante, mas não chegou a zero, o que indica que ele não tem a função de seleção de características
  • Esta é uma forma de regularização e usa-se a regularização L2.

• 6. Regressão de Lasso

  É semelhante à regressão de coluna, o Lasso (Least Absolute Shrinkage and Selection Operator) também penaliza o tamanho do valor absoluto do coeficiente de regressão. Além disso, é capaz de reduzir o grau de variação e melhorar a precisão do modelo de regressão linear. Veja a seguinte fórmula:

  

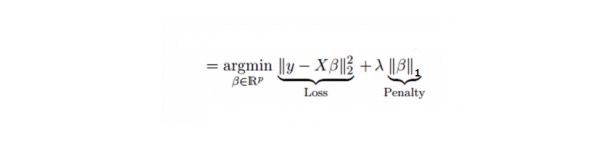
  A regressão de Lasso é um pouco diferente da regressão de Ridge, que usa a função de punição como um valor absoluto, e não um quadrado. Isso faz com que a punição (ou a soma dos valores absolutos da estimativa de constrangimento) faça com que alguns parâmetros sejam iguais a zero.

  A questão é:

  • A menos que seja um número constante, essa regressão é assumida de forma semelhante à regressão de menor quadruplo.
  • Tem um coeficiente de contração próximo de zero (equivalente a zero), o que realmente ajuda na seleção de características;
  • É um método de regularização que usa a regularização L1;
  • Se um conjunto de variáveis de previsão for altamente correlacionado, Lasso seleciona uma delas e reduz as outras a zero.

• 7. Regresso da ElasticNet

  O ElasticNet é um híbrido das técnicas de regressão de Lasso e Ridge. Ele usa o L1 para treinar e o L2 é priorizado como a matriz de regularização. O ElasticNet é útil quando há várias características relacionadas. O Lasso escolhe uma delas ao acaso, enquanto o ElasticNet escolhe duas.

  

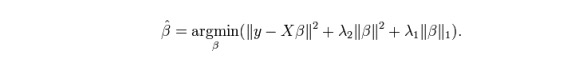
  A vantagem prática entre o Lasso e o Ridge é que ele permite que a ElasticNet herde alguma da estabilidade do Ridge no estado de ciclo.

  A questão é:

  • Em casos de variáveis altamente correlacionadas, ela produz efeitos de grupo;
  • Não há limite para o número de variáveis selecionadas;
  • Pode suportar uma contração dupla.
  • Além das sete técnicas de regressão mais usadas, você também pode ver outros modelos, como a regressão bayesiana, ecológica e robusta.

• Como escolher um modelo de regressão correto?

  A vida geralmente é mais fácil quando você só conhece uma ou duas técnicas. Uma instituição de treinamento que conheço disse a seus alunos que se os resultados são contínuos, use regressão linear. Se for binário, use regressão lógica.

  Em modelos de regressão múltipla, é importante escolher a técnica mais adequada com base no tipo de variável e variável, dimensões dos dados e outras características básicas dos dados. Os seguintes são os fatores-chave para escolher o modelo de regressão correto:

  A exploração de dados é parte indispensável da construção de modelos de previsão. Deve ser um passo prioritário na seleção de modelos adequados, como a identificação de relações e influências de variáveis.

  Para comparar os benefícios de diferentes modelos, podemos analisar diferentes parâmetros indicadores, como parâmetros de significância estatística, R-square, Adjusted R-square, AIC, BIC e pontos de erro, e outro é o Cp de Mallows. Isso é feito principalmente comparando o modelo com todos os possíveis submodelos (ou selecionando-os com cuidado) e examinando os possíveis desvios em seu modelo.

  A verificação cruzada é a melhor maneira de avaliar o modelo de previsão. Divida o seu conjunto de dados em duas partes (uma para treino e outra para verificação). Use uma simples equação entre o valor de observação e o valor de previsão para medir a precisão da sua previsão.

  Se o seu conjunto de dados é de variáveis mistas, então você não deve escolher o método de seleção automática do modelo, pois você não deve querer colocar todas as variáveis no mesmo modelo ao mesmo tempo.

  Também dependerá do seu objetivo. Pode ocorrer uma situação em que um modelo menos robusto é mais fácil de implementar do que um modelo com alta significância estatística.

  Os métodos de regularização de regressão ((Lasso, Ridge e ElasticNet) funcionam bem com múltiplas covalências entre variáveis de datasets de alta dimensão.

Traduzido de CSDN