A história de "fuga" e "sobrevivência" no jogo e no investimento
 1
1
 2878
2878
A história de “fuga” e “sobrevivência” no jogo e no investimento
** Quando se fala em jogo e investimento, as pessoas geralmente estão ansiosas para aprender os truques de ganhar dinheiro, na verdade, eu acho que ganhar dinheiro não é fácil de aprender, requer experiência e discernimento. Os iniciantes que querem melhorar rapidamente o parágrafo devem primeiro praticar a defesa. A primeira coisa a se preparar para escrever uma série de histórias sobre a fuga da escola é não ensinar as crianças a faltar às aulas, mas discutir com os colegas e os colegas sobre a aprendizagem sobre a fuga da escola. Inspirado em uma entrevista que fiz há três anos com o semanário “Red Weekly” de Hong Kong. Com a orientação do repórter, eu expus minhas ideias sobre o negócio de investimentos e negociações, publiquei uma grande teoria sobre a situação financeira da economia mundial e, por sinal, falei sobre algumas ideias de negociação. Achei que iria aparecer diante dos leitores como um especialista visionário de Hong Kong.
- ### Segredo de fuga do pai de Fishiang, o maior manipulador de Wall Street
Um pouco deprimido.
No entanto, pensar com cuidado, mas ter que admirar a agudeza do editor do repórter. Como os investimentos americanos ganham dinheiro com o povo chinês é um pouco distante, o grande argumento da situação não é pior do que o meu, o risco de fuga é um assunto relativamente vazio. Isso soa um pouco estranho, mas é vital para o sucesso do investimento a longo prazo.
O professor Wu Qiang pode começar com um enigma do senhor Liu Ka, fazer um enigma de aprendizagem seguindo o caminho de Holmes, Liu disse que ele também poderia começar com o enigma da fuga da vida, desenvolver um enigma de aprendizagem de fuga. A entrevista de mais de mil palavras de Liu Hong no semanário Liu Hong começou, agora vamos começar a falar.
Antes de começar, dê-me as boas-vindas: estou um pouco distraído, mas se for longe, até à vista.
Recentemente, descobri que a parte que mais interessava a muitos leitores sobre o mundo de Wall Street era a parte inicial sobre o jogo ((antes, os comerciantes de Londres enviaram uma versão eletrônica para amigos que deixaram o seu caixa de correio, na esperança de ajudar a todos). Parece que o ponto 21 afinal é mais próximo do público do que a queda das taxas de juros. Na verdade, o jogo e o investimento são muito semelhantes, e a experiência no cassino também me ajudou muito como comerciante na Wall Street.
A vida é o mais importante.
Quando se trata de apostas e investimentos, as pessoas geralmente estão ansiosas para aprender os truques de ganhar dinheiro. Na verdade, eu pessoalmente acho que o método de ganhar dinheiro não é fácil de aprender, requer muita experiência e discernimento.
Em suma, não se pode sacrificar antes da vitória da revolução. Não pense que isso é fácil de fazer, sem mencionar que todos os nossos amigos e companheiros de negócios que se enriqueceram tentaram morrer antes de nós, mesmo entre os mais altos da indústria de investimentos, há muitos que caíram do céu.
Veja alguns exemplos:
Jesse Livermore: O protagonista do livro de memórias de um investidor de ações, o gênio da especulação, que começou de mãos vazias e chegou a ter uma fortuna de US$ 100 milhões em 1929, acabou por pedir falência e suicidou-se alguns anos depois.
John Merryweather: ex-supertrader da Goldman Sachs e fundador do fundo de longo prazo LTCM, que em tempos tinha um capital de US$ 4 bilhões, mas foi quase totalmente destruído na crise de títulos da Rússia em 1998.
Tong Jingjun: Fundou a Universal Securities em 1988, foi conhecido como o pai da bolsa de valores da China, mas perdeu a liderança na China em 1995 com o incidente da dívida nacional de 3,27, e ficou preso.
Tang Wanxin: O antigo grupo empresarial da família Dron, que se orgulhava do mercado de capitais chinês, acabou se desintegrando devido à ruptura da cadeia de capitais que levou ao colapso do Império Dron.
Todos os que foram mencionados acima são gênios do mercado de capitais, mas todos acabaram por falhar. A experiência deles nos diz que, se não tomarmos cuidado para controlar os riscos, o que acontece é o mesmo que aconteceu com o pescador de peixe e o peixe-dourado: lutamos para sermos papas e, por fim, voltamos para a cabana à beira-mar.
O mais importante é estar vivo.
Não sei, não sei o que fazer.
Muitos anos atrás, eu costumava viajar de Chinatown, em Nova York, para Atlantic City, em um ônibus cheio de dinheiro, com a maioria dos trabalhadores que trabalhavam nos corredores dos restaurantes. Muitos deles tentavam mudar o destino nos cassinos, mas geralmente recebiam um salário insignificante. Lembro-me de uma vez que uma garota do meu bairro disse que ela ia ao casino todas as semanas para jogar pelicano e ganhar um conjunto de quebra-cabeças.
Eu ganhei 800 dólares e ela perdeu 4000. Eu fiquei muito feliz, 4000 dólares deveriam ser mais de um mês de receita dela! Olhando para o carro cheio de simpáticos compatriotas, de repente eu me senti triste, com ódio por aqueles que fazem negócios que enriquecem, é como enviar ovelhas para a boca do tigre! Eu tentei dizer à menina que jogar o jogo da loteria por um longo tempo e perder o dinheiro, mas ela não acreditou, disse que o dinheiro era apenas má sorte, e que deveria voltar a ler o livro na próxima semana.
Eu não tenho palavras, muitos fracassados usam a sorte como desculpa.
Uma vitória perdida é realmente sorte, 10.000 vitórias perdidas é um grande teorema matemático (o que tem maior chance de vitória quase sempre vence). Em jogos de cassinos em que os cassinos mantêm a probabilidade de vantagem, apostar repetidamente e perder não é apenas uma questão de tempo? Por isso, há um ditado: o cassino não tem medo de você ganhar, tem medo de você não vir.
O mesmo vale para o investimento.
O mercado de ações é melhor do que o cassino, a longo prazo deve ser um jogo de retorno positivo. Mas, devido a fatores como o jogo, negociações secretas e impostos sobre o consumo, o investidor comum se arriscar com muita frequência, a taxa de retorno é difícil de ganhar o mercado, e até mesmo pode perder. Portanto, não acredite nos chamados segredos secretos dos que ensinam a ganhar dinheiro rápido no mercado, 99% são flutuantes e 99% são negligentes.
Na era do Japão da Era Edo, um guerreiro chamado Shinya Bunbō, que lutou com o homem mais de sessenta vezes, nunca foi derrotado. Além de ser excelente em sua habilidade, ele também tinha um segredo: nunca brincar com alguém mais forte do que ele.
Não sei, não sei o que fazer.
É a primeira coisa que hackers e investidores devem ter em mente.

Qual é a vantagem do cassino?
O casino não tem medo de você ganhar, tem medo que você não venha, porque o jogo de casino é basicamente um jogo de azar. Muitos jogadores acreditam em sorte, enquanto os que operam o casino acreditam em probabilidade, que é a diferença entre o vencedor e o perdedor.
Por exemplo, no jogo de roulette (veja a figura abaixo), os jogadores podem apostar em qualquer número, e se a bola no rolo parar exatamente nesse número, o cassino ganha 35 vezes.
Parece tentador, não é?
O jovem que fugiu da Europa no filme Casablanca foi detido por 22 vezes e teve de pagar a viagem para os Estados Unidos.
Vamos fazer uma análise.
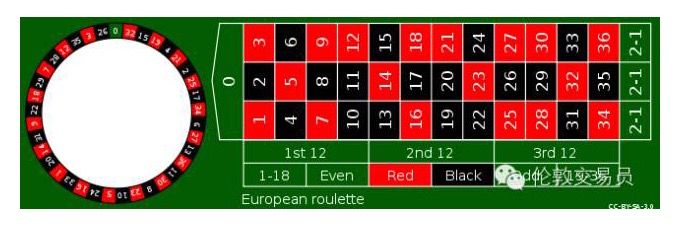
Se os 36 números são apenas 1 a 36, o jogador aposta 1 dólar por cada vez, ganha uma média de 36 vezes, ganha 35 dólares e compensa o dinheiro perdido por outras 35 vezes. Mas o cassino adiciona uma moeda 0 na esquerda do rolo, a face de ganho do jogador torna-se 1⁄37, ganha 35 dólares não é suficiente para compensar o dinheiro perdido por outras 36 vezes, o cassino ocupa 1⁄37 = 2,70% de vantagem de probabilidade, ou seja, cada jogador aposta 100 dólares e perde 2,7 dólares em média.
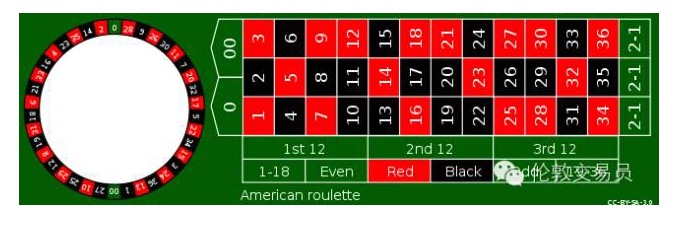
Além de apostar em números individuais, o roulette também tem apostas em vermelho e preto. Seja um número individual de 1x35 ou um preto de 1x1, a vantagem do cassino é a mesma. Mas há uma diferença importante entre os dois: a variação de perdas e ganhos de apostas em números individuais é claramente maior do que a de apostas em vermelho e preto.
Para começar, um breve comentário: a vantagem e a volatilidade são as duas coisas mais importantes no jogo e no investimento.
É melhor não tocar no jogo de que o ganhador deve perder, pois o jogo tem uma grande volatilidade; o investimento no jogo de que o ganhador deve ganhar deve ter uma pequena volatilidade. Sobre este princípio, será discutido em detalhes a seguir.
De volta ao jogo de azar, a maioria dos jogos de cassino são projetados de forma semelhante ao jogo de roleta: o cassino tem uma vantagem de probabilidade. Nestes jogos, os jogadores podem ganhar dinheiro com sorte se jogar apenas algumas mãos, e quase certamente perderão se jogar por muito tempo, o que na matemática é chamado de lei dos grandes números.
No entanto, os matemáticos encontraram uma falha no cálculo do número de caça-níqueis.
Histórias antigas de 21 horas
No início dos anos 1960, um matemático americano chamado Edward Thorp usou o recém-aparecido computador para encontrar oportunidades no jogo de 21 pontos, desenvolvendo um método para vencer o cassino através da contagem de cartas. O professor Thorp colocou a teoria em prática, usando sua própria contagem de cartas para vencer o cassino, e logo foi incluído na lista negra, e alguém escreveu um livro!
O livro de Thorpe, Beat the Dealer, vendeu 700 mil cópias e ficou no topo da lista de livros mais vendidos do New York Times. O autor ficou envergonhado, lembrando-se de outros livros tão bem vendidos como o de Wall Street. A receita de impostos sobre o copyright é muito maior do que a receita de jogos de azar.
O princípio da conta de cartas de Thorp não é difícil. Primeiro, a regra de 21 pontos: o jogador e o cassinista (casino) se enfrentam, para ver quem está mais próximo da soma de pontos das cartas na mão (mas não mais do que) 21 pontos. 10, J, Q, K são dez pontos, e de 2 a 9 são contados de acordo com os pontos respectivos.
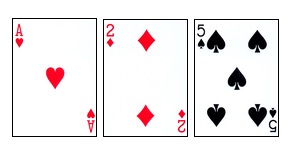
O jogo de cartas começa com o jogador e o casal de apostas a distribuir duas cartas cada, e a carta do casal é clara ou escura (como na figura abaixo). Em seguida, o jogador decide: pode fazer ações especiais, como cravar, dobrar, ou optar por parar o jogo a qualquer momento. Se o jogador ultrapassar 21 pontos (cravando a carta), perde diretamente, caso contrário, o jogo é interrompido após o jogo de apostas.
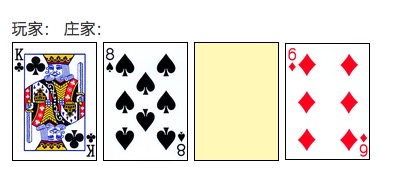
Além disso, há uma regra especial: uma carta A e uma carta de dez pontos ((10, J, Q, K) são chamadas de Black Jack (Blackjack), e o ganhador ganha diretamente. Se o jogador tiver um Black Jack, pode ganhar 1,5 vezes o chip.
É óbvio que o casal e o jogador têm vantagens em um jogo de 21 pontos. A vantagem do casal é que o casal pode ganhar sem lutar se o jogador esbarrar primeiro. A vantagem do jogador está na flexibilidade de movimentos, que pode decidir a estratégia de acordo com sua própria carta e a carta exposta pelo casal.
Quanto maior o número de cartas de dez pontos e A, maior a chance de blackjack, e maior a probabilidade de quebrar, o jogador tem mais vantagem em jogar de forma dinâmica e flexível. Por outro lado, quanto maior o número de cartas pequenas, como 3, 4, 5, 6 e assim por diante, menor a probabilidade de quebrar, o que é mais favorável para o casal.
O 21 da era Thorpe era mais usado com um ou dois pares de cartas de pôquer, e quando as cartas eram limpas, o cassino tinha uma vantagem de probabilidade de cerca de 0,5%. O segredo é que, à medida que o jogo avança, a proporção de cartas grandes e A, em alguns momentos, fica alta e a probabilidade se transforma em favor do jogador.
O monge Thorpe inventou o jogo de cartas, escreveu um livro que se tornou um best-seller, e, depois de se ter apercebido, tornou-se rico em Wall Street e, mais tarde, criou um mundo no setor de fundos de cobertura.
Quanto ao lado do cassino, desde então, surgiu um grupo de contadores de cartas que dominaram o Sousuke Wujong. O lado do cassino tentou fazer tudo o que podia para rejeitar os contadores de cartas, e os contadores de cartas fizeram o possível para quebrar o bloqueio. O jogo do gato e do rato foi jogado por décadas, antes e depois da década de 90, e um novo fenômeno aconteceu no Lago Yang.
(Lembre-se, a narrativa acaba por retornar ao investimento).
O grupo de cartões do MIT
Falando de Thorpe, o casino teve um problema com um contador de cartas. Ao longo do tempo, o casino acumulou uma lista negra. Se alguém na lista fosse reconhecido na mesa de 21 cartas, normalmente seria imediatamente expulso do país.
Em algum momento da década de 1980, os detetives contratados pelo cassino juntaram as listas negras coletadas em todos os lugares e descobriram uma pista importante: o endereço de muitos contadores de cartas estava perto da cidade de Cambridge, Massachusetts! Cambridge, Massachusetts, você pode não ter ouvido falar, mas as duas universidades localizadas aqui você não pode ter ouvido falar: Harvard, MIT.
A verdade veio à tona quando um grupo de estudantes do MIT começou a jogar cartas.
Esta é uma organização que funciona como uma maquiagem comercial: alguém faz o capital, alguém é responsável pela administração, alguém joga as cartas, toda a maquiagem é investida e a maquiagem é um modelo de controle de risco, tem o estilo de um fundo de hedge. O maior benefício da maquiagem em grupo é que você pode evitar o risco que o único hacker enfrenta: a volatilidade de ganhar e perder é grande: 21 pontos, quanto mais técnica você for, a má sorte no curto prazo pode perder o capital, a batalha do grupo pode dispersar esse risco. Além disso, os hackers do MIT também usam algumas técnicas de maquiagem de batalha multi-pessoais.
Por exemplo, Michael, que contava as cartas e fazia pequenas apostas, lançava criptomoedas previamente combinadas quando a situação era favorável, enquanto James, disfarçado de James, aparecia e fazia uma aposta de US$ 1.000.
O grupo do MIT operou por mais de uma década, com a participação de pessoas de universidades como o MIT e o Harvard, incluindo chineses que ganharam medalhas de ouro nos Jogos Olímpicos. Os soldados de ferro que jogam água no baralho, de qualquer maneira, o mais indispensável em Cambridge, Massachusetts, é o gênio da matemática. O lucro do grupo foi relatado em milhões de dólares, e mais tarde um escritor escreveu um livro que englobava os feitos do grupo do MIT, que também entrou na lista de best-sellers do New York Times.
Em meados da década de 1990, a economia americana estava em alta, os membros dos gangs viajavam para o Vale do Silício, Wall Street e outros lugares, e os gangs do MIT começaram a se dispersar. Isso também parece provar uma verdade: os jovens têm um bom emprego, e a taxa de criminalidade diminui.
Depois de alguns anos, os colegas de Fuchang, da China, encontraram por acaso o jogo de cartas de 21 pontos, e ficaram muito interessados. Na época, eu não tinha ouvido falar de Soup e não sabia que o livro do mestre Soup era vendido por apenas uma dezena de dólares, e gastei US$ 100 para comprar o chamado livro de segredos de yoga de um grande jogador chamado Kadosa. Apesar de ter sido esfaqueado por um macaco de alto preço, apesar de ter um macaco, também fui ao cassino para cavar ouro!
Mas o lago não é o mesmo daquele ano.
Confusão sobre apostas
Depois de aprender a contar cartas, eu fui com entusiasmo para Las Vegas para testar a faca do touro. O resultado foi ótimo, ganhei uma pilha de cem dólares, o que é uma mina de ouro! Eu moro em Nova York, e não posso ir sempre a Las Vegas para minar ouro, pois a cidade de Atlantic City, a segunda maior cidade de ouro dos Estados Unidos, também está perto de Nova York, então eu me tornei um visitante regular de lá.
Depois de algum tempo, comecei a perceber que o Atlantic City era um lugar de areia de alumínio que não era fácil de escolher, que eu só conseguia ganhar pouco e perder muito. Depois de um estudo mais minucioso, descobri que Atlantic City não era como Las Vegas.
Como mencionado anteriormente, o contador de cartas se baseia principalmente na proporção de cartas grandes e pequenas no restante da carteira, e quando a proporção de cartas grandes é maior do que o normal, ele faz uma grande aposta.
Obviamente, a proporção é mais fácil de aumentar em duas situações, a primeira é quando não há muitas cartas restantes, a segunda é quando o jogo de 21 pontos usa apenas 1-2 cartas de apoio. O jogo de 21 pontos da era Thorpe tem exatamente essas duas características: apenas 1-2 cartas de apoio, e o distribuidor (o dealer) vai lavar as cartas quase com a luz, então a proporção da grande carteira é sempre alta, e o contador de cartas tem muitas oportunidades de apostar quando a situação é favorável.
Naturalmente, o casino também tem um planejamento de pessoas de alto escalão, que entendem que a melhor defesa suave para a contagem de cartas é tentar controlar a oscilação da proporção de cartas grandes e pequenas, então o casino fez duas medidas venenosas. A primeira é o aumento de 21 pontos de cartas, de 1-2 pares para 6-8 pares.
É óbvio que, se houver mais cartas, a proporção de cartas grandes e pequenas não vai mudar facilmente.
O segundo é a lavagem antecipada de cartas, evitando a situação mais fácil de oscilação das proporções. Os casinos de Las Vegas são muitos e competitivos, os casinos reservam alguns jogos de 21 pontos com 1-2 cartas de duplas para os apostadores, e eu ganho dinheiro principalmente nessas apostas.
O meu lago não é mais o lago que era no tempo de Thorpe.
Mesmo assim, quando as proporções aumentam, eu ainda ganho no cassino. Já falei sobre a lei da maioria de Liu: desde que haja uma vantagem, em teoria, eu vou continuar jogando no final ou eu ganho. Mas a teoria é teoria, na prática há uma restrição importante: minha aposta é limitada e não posso jogar se perder. A lei da maioria apenas diz que a revolução do quiabo acabará vencendo, mas não garante que você não sacrifique o quiabo antes da vitória da revolução do quiabo.
Suponha que eu ganhei apenas US$ 10 mil, e não é fácil esperar até que eu tenha uma vantagem de 1% sobre o cassino.
Place your bets.
Quanto é que eu aposto? 20 dólares? Em média ganho apenas 2 centavos, não quero dizer isso.
Eu perdi a luz ao pegar um cisne que não era muito preto (perdi 5 vezes seguidas). Parece que 20 dólares é muito pouco, 2000 dólares é muito, e a melhor aposta deve ser entre os dois.
A resposta já foi dada por um dos grandes.
(Vamos falar sobre a teoria do investimento).
Fórmula de Kelly
O que é uma aposta apropriada? Em 1956, o cientista Kelly (John Kelly) publicou um artigo sobre isso, apresentando a famosa fórmula de Kelly.
f* = (bp - q) / b Destes, f* = proporção do montante investido em relação ao capital total p = probabilidade de ganhar q = probabilidade de falhar, q = 1-p b = probabilidade, por exemplo, apostar num único número na roda do roulette, b = 35, apostar no vermelho e no preto, b = 1。
No problema de apostas de 21 pontos mencionado no artigo anterior, assumindo que o total de apostas é de US$ 10.000, e que a probabilidade de vencer é de 51%, com uma diferença de 1:1 (a diferença entre a probabilidade de ganhar e a probabilidade de perder é pequena, mas não muito grande), então a melhor aposta dada pela fórmula de Kelly é:
\(10000 * (1 * 0.51 - 0.49)/ 1 = \)200 Eu sei que muitas pessoas ficam surpresas ao ver fórmulas matemáticas, mas para jogar e investir, é necessário aprender matemática. O mais importante não é calcular números com fórmulas, mas entender o verdadeiro significado por trás delas.
Em primeiro lugar, a bp - q da molécula na fórmula representa a probabilidade de ganhar o jogo, que é chamado de expectativa, a fórmula de Kelly afirma que só se pode apostar no jogo do valor esperado positivo, que é o princípio mais básico de todos os jogos de azar e investimentos, ou seja, o jogo de azar mencionado anteriormente não tem certeza, nunca se aposta.
Em segundo lugar, a probabilidade de ganhar é dividida pela probabilidade de ganhar. Ou seja, com a mesma probabilidade de ganhar, quanto menor a probabilidade, mais se pode apostar.
O Botafogo: 20% de chances de ganhar, 1 de perder e 5 de perder.*20% - 80% = 20% A probabilidade de ganhar é de 60%, 1 a perder é de 1 . bp - q = 1*60% - 40% = 20% A probabilidade de ganhar é de 80%, 1 contra 0,5 ◦ bp - q = 0,5*80% - 20% = 20%
O valor esperado matematicamente para os três jogos é de 20%, ou seja, apostar 100 dólares ganha 20 dólares em média. De acordo com a tenacidade da maioria dos países, talvez seja melhor escolher o jogo do pequeno jogo do grande jogo, não é? Mas dividindo o jogo do pequeno jogo do grande jogo pelo jogo do b da fórmula de Kelly, o jogo do pequeno jogo do grande jogo pode apostar apenas 4% do capital total, o jogo do meio do jogo pode apostar 20%, o jogo do grande jogo pode apostar 40%.
Na realidade, a maioria dos jogadores de bingo são piratas.
Quem gosta de apostar em jogos de azar?
Os investidores profissionais de Wall Street também jogam muito com o jogo de apostas, pois é mais fácil usar a alavancagem. Mais sobre isso mais adiante.
Finalmente, a fórmula de Kelly indica a importância crucial do controle de risco: mesmo em jogos com um valor de expectativa positivo, não se deve apostar muito. Matematicamente, a proporção de dinheiro apostado é superior ao valor de Kelly, e a taxa de ganho de dinheiro a longo prazo, pelo contrário, diminui, aumentando significativamente a probabilidade de perdas catastróficas.
Por que é que os investidores perderam a vida a favor de alguns velhos proprietários de tecnologia local? A maioria das razões é que eles apostaram muito dinheiro.
Livermore perdeu para Macy’s
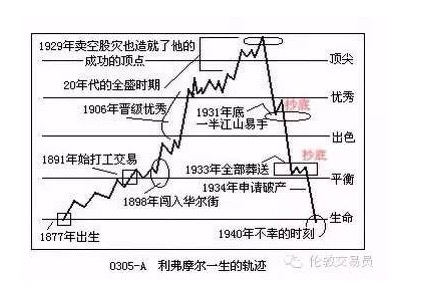
Em 28 de novembro de 1940, 16 anos antes da publicação da fórmula de Kelly, um ex-solista de Wall Street tirou uma pistola do armário do Waldorf Hotel, em Nova York, e deixou uma nota para sua esposa: “Olha… estou cansado de lutar… é a única libertação.
Jesse Livermore, o protagonista do livro de memórias do inventor de ações, morre de tristeza.
Se você ainda não leu o livro de memórias de um operador de ações, eu recomendo fortemente que você faça isso. Muitos gerentes de fundos de cobertura de classe mundial são muito admirados por este livro.
Ele resumiu muitas das leis que os investidores modernos consideram clássicas, como: adicionar dinheiro quando você ganha, parar quando você perde, não desprezar a opinião de outras pessoas ou o que é chamado de propaganda de insider, e um conjunto completo de estratégias de negociação.
Mais impressionante ainda, Livermore não era apenas um teórico, mas também um praticante. Sua vida de negócios variou, de milhões de dólares em 1907 para 100 milhões de dólares em 1929! Naquela época, os carros vendiam apenas algumas centenas de dólares por carro, e Livermore ganhou 100 milhões de dólares apenas com o comércio, o equivalente a mais de 10 bilhões de dólares hoje!
Como um gênio que não se destacou, mas depois perdeu uma fortuna enorme no mercado, ele acabou com a triste cena que começa este artigo. Como é que Livermore foi para o McDonald’s?
A carreira de Livermore começou no Bucket Shop.
No final do século XIX, o mercado de ações dos Estados Unidos era muito ativo, e os avanços tecnológicos permitiram que pessoas comuns longe de Nova York também pudessem participar de especulações de ações em tempo real: uma máquina de cotação automática conectada a um telégrafo poderia transmitir o preço mais recente da Bolsa de Nova York para todo o país.
Existem máquinas de cotação automática no cassino, onde os jogadores parecem estar negociando ações, que na verdade são do tamanho de uma moeda. Por exemplo, a oferta mais recente de uma ação é de US \( 80, e o jogador pode comprar uma moeda de ouro com apenas US \) 1 em garantia. Se o preço for de US \( 79 ou menos, então você perdeu a luz; se o preço for de US \) 81, o jogador pode ganhar US $ 1 em lucro, e assim por diante.
Como é que os bandidos dos casinos de ações ganham dinheiro?
Além de aproveitarem-se da característica de que as massas costumam apostar errado, eles também conspiram para manipular o mercado de certos corretores. Por exemplo, muitos jogadores apostaram em um preço de US $ 80 para ganhar um grande prêmio, e os corretores do cassino indicaram que seus colegas da bolsa de Nova York pressionaram o preço das ações.
Naquela época, o jovem Livermore não tinha muito dinheiro, mas se envolveu no jogo de ações e gradualmente aprendeu a prever o preço do mercado com base na oferta (Read Tape). Naquela época, não havia computadores e nem gráficos K em tempo real.
Mas suspeito que ele também tenha desenvolvido um mau hábito no cassino de ações: apostar muito.
Analisado do ponto de vista da fórmula de Kelly, o bônus ultra-baixo do cassino de ações era o assassino dos jogadores. A alavancagem era tão grande que a aposta era muito superior ao bônus de Kelly, e a perda era cedo ou tarde. O bônus de transação do mercado financeiro formal dos EUA na época também era baixo.
O seu histórico de negociação é impressionante, as ações, o algodão, a soja, o que quer que seja uma operação de alta alavancagem total, o que fez com que o lendário Liverpool fosse grande, mas também o levou a falência várias vezes. Felizmente, com a ajuda de alguns nobres, o Liverpool conseguiu aproveitar algumas oportunidades importantes para atingir o pico em 1907, 1915 e 1929.
Mas, no final das contas, o sábio teve um erro, e eu suspeito que foi o erro de apostar muito que fez com que Livermore perdesse tudo em apenas alguns anos depois de atingir o valor de US$ 100 milhões.
O que é que este génio poderia fazer se combinasse a sua metodologia de gestão de fundos baseada na fórmula de Kelly com a sua habilidade de controlar os mercados?
A história não tem se.
Livermore já passou como um meteoro, talvez com décadas de idade.
As teorias de gestão de fundos e controle de risco só começaram a se formar nos anos 50.
A fórmula de Kelly afirma que jogos com grandes margens de lucro e pouca volatilidade permitem apostas maiores. Então, como quantificar as grandes margens de lucro e as pequenas volatilidades? Um estudioso contemporâneo de Kelly propôs um indicador famoso.
Relação de Sharpe
Em 1966, o acadêmico William Sharpe propôs o famoso índice de Sharpe com base nisso:
S = (R r) / σ, onde: R = retorno esperado do investimento (retorno médio) r = taxa de retorno de um investimento sem risco (que pode ser entendida como a taxa de retorno de um investimento em dívida pública) σ = Divergência padrão da taxa de retorno (o indicador estatístico mais utilizado para medir a volatilidade)
Quanto maior o índice de Sharpe, maior a qualidade da oportunidade de investimento. Por exemplo:
Investimento A: Retorno esperado de excedentes (mais do que a dívida pública) de 10%, diferença padrão de 20%, taxa de Sharpe de 0,5 Investimento B: Expectativa de retorno excedente de 5%, diferença padrão de 5%, taxa de Sharpe de 1
À primeira vista, a expectativa de retorno do investimento em A parece ser uma boa oportunidade. Na verdade, o investimento em B é melhor do que o Sharpe ratio (normalmente), pois sua alta taxa de Sharpe significa que o investidor pode trocar 1 unidade de risco de um investimento em A por uma expectativa de retorno maior. A mesma conclusão pode ser tirada do ponto de vista do investimento em alavancagem: assumindo que o investidor financie com uma taxa de juros de empréstimo r, duplicando a alavancagem em uma oportunidade de investimento em B, o investimento em A com alavancagem torna-se uma expectativa de retorno de 10%, com um diferencial padrão de 10%, o mesmo que a expectativa de retorno do investimento em A, com menor risco.
Qual é o índice de Sharpe para ser um bom jogador?
Vejamos um exemplo real: o mercado de ações dos EUA tem uma média de retorno anual de aproximadamente 10%, uma volatilidade de aproximadamente 16%, uma taxa de juros sem risco de aproximadamente 3.5%, portanto, um índice de Sharpe de aproximadamente 0.4 (fonte: Wikipedia). Em outras palavras, o índice de investimentos em ações dos EUA tem uma taxa de retorno anual de aproximadamente 6,5% acima da taxa de juros sem risco, mas uma média de retorno de um ano em 6 anos é inferior a -6% (além de 1 multiplicador).
Para os investidores a retalho, o risco/retorno das ações americanas é um passado. Para os gestores de fundos de cobertura, esse Sharpe ratio é muito baixo: se você tiver como meta uma taxa de retorno anual de 20%, terá que usar 2,5 vezes mais de alavancagem (a expectativa de retorno = 2,5).*10% - 1.53,5% ≈ 20%), significaria que, em média, um ano em cada seis anos, a taxa de retorno seria inferior a 2,5.(10% - 16%)- 1.5*3.5% = -20% . Se você perder mais de 20%, o cliente provavelmente ficará sem dinheiro .
Em geral, o Sharpe Ratio superior a 1 é um bom jogo de jogo. Esta oportunidade não é comum em um jogo de investimento simples, portanto, os investidores profissionais costumam usar métodos de hedge para modificar o jogo de investimento de jogo e melhorar o Sharpe Ratio.
Por exemplo, se você inventou uma maneira de usar vários ativos para se contrabalançar e obter uma oportunidade de investimento com um Sharpe ratio de 2, então você pode arriscar a alavancagem (os colegas que são bons em matemática podem calcular a probabilidade de perder dinheiro sozinhos) e os investidores provavelmente irão investir em seu fundo de hedge.
No entanto, o método de investimento com cobertura e alavancagem geralmente tem um obstáculo: é necessário tomar muito dinheiro emprestado e exigir muita liquidez, o que geralmente causa problemas em crises súbitas, como o LTCM e o Global Alpha Fund da Goldman Sachs, analisados no Wall Street Journal.
A proporção de Sharpe também tem uma falha, pois assume que o retorno é normal, enquanto a distribuição de retorno de investimento real tem um rabo de cavalo de gordura (a probabilidade de perder muito dinheiro é maior do que a estimativa da distribuição normal), portanto, há um problema em escolher oportunidades de investimento simplesmente com base na proporção de Sharpe e é fácil de ser manipulada por um rabo de cavalo. Este tópico não será discutido aqui.
Para os investidores comuns, a proporção de Sharpe sugere que os investimentos que são mais rentáveis sejam escolhidos com base na combinação de risco e retorno. É exatamente o ponto de vista mencionado no artigo anterior: escolha um jogo de retorno positivo com pouca volatilidade, escolha um jogo de retorno negativo com grande volatilidade se for necessário.
A proporção de Sharpe fala sobre como escolher um jogo de cartas, enquanto a fórmula de Kelly fala sobre como escolher as apostas depois do jogo para obter a melhor taxa de retorno a longo prazo.
Nota complementar sobre a proporção de Sharpe
O problema com o Sharpe ratio está centrado em vários aspectos:
Primeira pergunta: Como é que se calcula o retorno médio de um ano de um dólar em menos de 6% no caso do dólar americano?
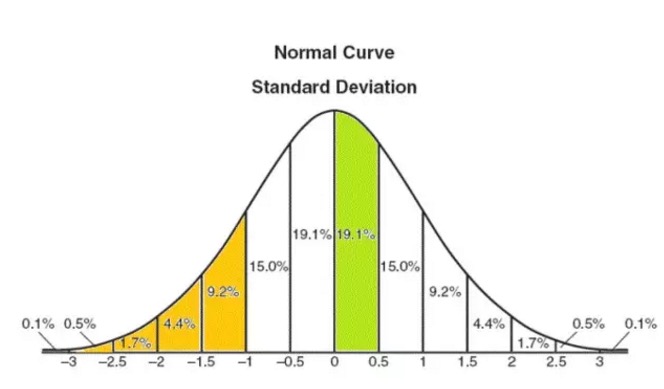
A proporção de Sharpe assume que o retorno do investimento corresponde a uma distribuição normal (veja a figura abaixo). Em termos matemáticos, a soma de um grande número de eventos aleatórios independentes corresponde geralmente a uma distribuição normal. Por exemplo, o resultado de um lançamento contínuo de moedas, face positiva é 1, face oposta é 1, a soma de um grande número de resultados após a repetição corresponde a uma distribuição normal.
A hipótese de uma distribuição normal, embora imperfeita, é o quadro básico para a compreensão do problema. O gráfico abaixo mostra os valores de probabilidade de uma distribuição normal. Por exemplo, a probabilidade de taxa de retorno entre 0 e 0,5 vezes o desvio padrão é de 19,1% (a parte verde do gráfico).
Da mesma forma, a probabilidade de retornos inferiores a 1x o desvio padrão (a parte laranja do gráfico) é de cerca de 16%. Aplica-se ao mercado de ações dos EUA (o valor médio de retornos é de 10%, o desvio padrão é de 16%) e a probabilidade de retornos anuais inferiores a 1x o desvio padrão, ou seja, 10% - 16% = -6%, é de cerca de 1⁄6.
A segunda pergunta é: há alguma contradição entre a hipótese da proporção de Sharpe e a realidade?
É claro que existe. A hipótese de distribuição normal não é perfeita. Na verdade, o movimento do mercado de ações não é completamente independente de um eixo aleatório, caso contrário, não precisamos nos preocupar em estudar nenhuma lei. Por exemplo, na crise financeira, o movimento do mercado de ações tem uma forte correlação em série, a chamada correlação de tendência de queda, que leva ao fenômeno de queda de tendência de queda, o que significa que a probabilidade de retornos do mercado de ações com um eixo de queda é maior do que a estimativa da distribuição normal.
Além disso, a taxa de retorno sem risco zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero zero
A terceira pergunta é: o que é que o Sharpe Ratio tem a ver com o investidor comum?
A próxima vez que alguém lhe disser que eu ganhei 30% em média nos últimos três anos, você pode perguntar, com timidez: “Quão volátil é a moeda?”
Exemplos de análise de resultados de fundos de cobertura
Para avaliar o desempenho de um investimento, não basta olhar apenas para a taxa de retorno, mas também para os fatores de risco. Vejamos agora um exemplo real de um fundo de hedge. A tabela a seguir mostra a média anual de retorno de vários grandes fundos de hedge conhecidos (fonte: HSBC Research Report).
Quadro 1
| - | - |
| - | Taxa de retorno anual |
| Fundo A | 14.15% |
| Fundo B | 15.17% |
| Fundo C | 15.20% |
| Fundo D | 79.17% |
| Fundo E | 2.78% |
Parabéns, você escolheu o Paulson Credit Opportunities Fund, que foi criado e administrado pelo ex-ministro das Finanças dos EUA Paulson (com o mesmo nome, mas sem parentesco) e tornou-se um dos mais famosos gestores de fundos.
Mas já discutimos: não podemos olhar apenas para a taxa de retorno, mas também para o risco. A Tabela 2 mostra a volatilidade e a taxa de Sharpe entre os fundos (assumindo que a taxa de retorno sem risco é de 3%).
Quadro 2
| - | Taxa de retorno anual | Variação da taxa de retorno | Relação de Sharpe |
|---|---|---|---|
| Fundo A | 14.15% | 5.94% | 1.9 |
| Fundo B | 15.17% | 12.30% | 1.0 |
| Fundo C | 15.20% | 4.53% | 2.7 |
| Paulson Credit Opportunities | 79.17% | 49.83% | 1.5 |
| Fundo E | 2.78% | 12.21% | <0 |
Em outras palavras, a volatilidade do fundo C é apenas um décimo da volatilidade do fundo Paulson, assumindo que o investidor está disposto a assumir apenas um risco de volatilidade fixo, então ele pode investir US \( 1 no fundo Paulson ou US \) 10 no fundo C, com o mesmo risco, e o retorno total do fundo C é maior!
O Fundo C é o Millennium Intl Ltd (Fundo Millennium), uma árvore perene da indústria de fundos de cobertura, com vários executivos de origem chinesa. Do ponto de vista dos investidores, é um pouco difícil escolher entre o Paulson Fund, que ganhou muito dinheiro, ou o Millennium Fund, que ganhou muito dinheiro. Além disso, o Sharpe ratio do Fundo A e do Fundo B é claramente superior ao de 0,4 do mercado de ações dos EUA, e é uma boa opção de investimento.
Em uma análise mais aprofundada, comparando apenas com a taxa de Sharpe, parece que a taxa de câmbio do fundo Paulson não é muito justa: embora seja alta, a sua volatilidade é principalmente a taxa de câmbio de câmbio de câmbio de câmbio de câmbio de câmbio de câmbio de câmbio de câmbio de câmbio de câmbio de câmbio de câmbio de câmbio de câmbio de câmbio de câmbio de câmbio de câmbio de câmbio de câmbio de câmbio de câmbio de câmbio.
Quadro 3
| - | Taxa de retorno anual | Variação da taxa de retorno | Relação de Sharpe | Maior queda (tempo de ocorrência) |
|---|---|---|---|---|
| Bluecrest | 14.15% | 5.94% | 1.9 | -4.83% (2003) |
| FORE (Capital de Frente) | 15.17% | 12.30% | 1.0 | -27.01%(2008) |
| Millennium (em inglês) | 15.20% | 4.53% | 2.7 | -7.24% (1998) |
| Paulson Credit Opportunities | 79.17% | 49.83% | 1.5 | -10.41%(2007) |
| Drake | 2.78% | 12.21% | <0 | -51.74%(2007-2009) |
Agora é mais interessante que o fundo A (Bluecrest Capital) teve o maior declínio de menos de 5%, e isso ocorreu em 2003. O fundo evitou grandes perdas durante a grande crise de 2007-2008, o que é bastante atraente. Tanto o Bluecrest quanto o Millennium são do tipo de investidores estáveis, que escaparam da crise de empréstimos secundários, e os dois parecem ser difíceis de separar.
Os três fundos são favoritos dos investidores institucionais, com US \( 8,6 bilhões, US \) 10 bilhões e US $ 6,3 bilhões, respectivamente. Parece que é razoável que as pessoas possam fazer grandes investimentos.
O fundo E (Drake Absolute Return Fund) também foi um grande fundo que gerenciava bilhões de dólares, mas sofreu uma perda enorme de mais de 50% durante a crise financeira, o que fez com que os investidores perdessem a confiança e retirassem os investimentos, então o capital gerenciado pelo Drake agora é de apenas US $ 200 milhões.
O fundo B, que tem uma taxa de retorno anual de 15%, um Sharpe ratio de 1, um bom índice de composição, e que, apesar de ter sofrido um prejuízo de 27% em 2008, conseguiu superar a crise. Pode-se dizer que o fundo B tem bastante força, então ele também se tornou um grande fundo que gerencia US$ 10 bilhões. O nome do fundo é FORE Capital, e o seu filho Matthew Li é um estandarte da comunidade de fundos de cobertura chinesa.
A partir deste exemplo real de avaliação do desempenho de investimentos, podemos ver a utilidade de indicadores de risco, como a taxa de Sharpe e a queda máxima. Os investidores iniciantes costumam ter o problema de considerar apenas o retorno e não o risco.
Os mercados de ações são arriscados e os investimentos devem ser feitos com cautela. A informação fornecida é apenas para referência e não constitui uma recomendação de investimento!
A transmissão foi feita pelo blogueiro de Fischer Yang, Sistochin.