Compreensão interessante de Naive Bayes

NavieBayes

  Muitas situações da vida exigem classificação, como classificação de notícias, classificação de pacientes, etc. Para que você possa visualizar a compreensão, este artigo apresenta um algoritmo de classificação simples e comumente usado a partir de aplicações práticas: o simples Bayes (Navie Bayes classifier).

• 01 Exemplo de classificação de pacientes

Deixe-me começar com um exemplo, e você verá que o classificador de Bayes é muito fácil de entender, não é nada difícil. Um hospital recebeu seis pacientes em consultas médicas pela manhã, como mostra a tabela abaixo.

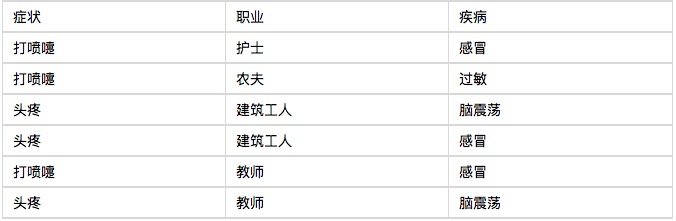
E agora vem o sétimo paciente, um trabalhador da construção que espirra. Pergunte-lhe qual é a probabilidade de ele ter um resfriado.

  P(A|B) = P(B|A) P(A) / P(B)

Não é verdade.

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏x建筑工人|感冒) x P(感冒) 
  　　　　/ P(打喷嚏x建筑工人)

Suponha que as características de “espirrar” e “trabalhador de construção” sejam independentes, e, portanto, a equação acima se transforma em

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒)
  　　　　/ P(打喷嚏) x P(建筑工人)

Isso pode ser calculado.

  P(感冒|打喷嚏x建筑工人) 
  　　　　= 0.66 x 0.33 x 0.5 / 0.5 x 0.33 
  　　　　= 0.66

Assim, o trabalhador de construção que espirrou teve uma probabilidade de 66% de ter tido uma gripe. Assim, a probabilidade de que o paciente tivesse uma alergia ou um concussão pode ser calculada. Comparando essas probabilidades, é possível saber qual a doença mais provável que ele teria.

Este é o método básico do classificador de Bayes: com base em dados estatísticos, com base em certas características, calcula-se a probabilidade de cada categoria, de modo a realizar a classificação.

• 02 Fórmula do classificador básio simples

Suponha que um indivíduo tenha n características, F1, F2, … , Fn. Existem m categorias, C1, C2, … , Cm. O classificador de Bayes é a classificação com maior probabilidade de ser calculada, ou seja, o valor máximo do seguinte algoritmo:

  P(C|F1F2...Fn) 
  　　   = P(F1F2...Fn|C)P(C) / P(F1F2...Fn)

Como P ((F1F2…Fn) é o mesmo para todas as categorias, pode ser omitido, e a questão torna-se

  P(F1F2...Fn|C)P(C)

Valor máximo de

O classificador básio simples é mais avançado, assumindo que todas as características são independentes umas das outras, e portanto

  P(F1F2...Fn|C)P(C) 
  　　   = P(F1|C)P(F2|C) ... P(Fn|C)P(C)

Cada elemento à direita da equação pode ser obtido a partir de dados estatísticos que permitem calcular a probabilidade de correspondência de cada categoria e, assim, descobrir a categoria com maior probabilidade.

Embora a hipótese de que “todas as características são independentes umas das outras” seja improvável na realidade, ela pode simplificar consideravelmente o cálculo, e há estudos que mostram que a precisão dos resultados da classificação é pouco afetada.

A seguir, vamos ver mais dois exemplos de como usar o classificador básio simples.

• 03 Classificação de contas

De acordo com uma amostra de estatísticas de um site de comunidade, 89% das 10 mil contas do site são reais (configure C0) e 11% são falsas (configure C1). Em seguida, os dados estatísticos são usados para julgar a autenticidade de uma conta.

  C0 = 0.89 C1 = 0.11

Suponha que uma conta possui as três seguintes características: F1: Número de diários/dias de registro F2: Número de amigos/dias de inscrição F3: Se a imagem real é usada (a imagem real é 1, a imagem não-real é 0) F1 = 0.1  F2 = 0.2  F3 = 0

O método é usar um classificador básio simples para calcular o valor da seguinte fórmula:

P(F1|C)P(F2|C)P(F3|C)P©

Embora os valores acima possam ser obtidos a partir de dados estatísticos, há um problema: F1 e F2 são variáveis contínuas e não são adequadas para calcular a probabilidade de acordo com um determinado valor. Uma técnica é transformar valores contínuos em valores dispersos e calcular a probabilidade de intervalos.[0, 0.05]、(0.05, 0.2)、[0.2, +∞] três intervalos, e calculamos a probabilidade de cada um deles. No nosso exemplo, F1 é igual a 0.1 e cai no segundo intervalo, então, quando o cálculo é feito, usamos a probabilidade de ocorrência do segundo intervalo.

De acordo com as estatísticas:

P(F1|C0) = 0.5, P(F1|C1) = 0.1  P(F2|C0) = 0.7, P(F2|C1) = 0.2  P(F3|C0) = 0.2, P(F3|C1) = 0.9

Portanto,

P(F1|C0) P(F2|C0) P(F3|C0) P(C0)  = 0.5 x 0.7 x 0.2 x 0.89  = 0.0623 P(F1|C1) P(F2|C1) P(F3|C1) P(C1)  = 0.1 x 0.2 x 0.9 x 0.11  = 0.00198 Pode-se ver que, embora este usuário não tenha usado uma imagem de rosto real, ele é mais de 30 vezes mais provável que seja uma conta real do que uma falsa, portanto, julgar a conta como verdadeira.

• 04 Classificação por sexo

A seguir estão algumas estatísticas sobre as características do corpo humano.

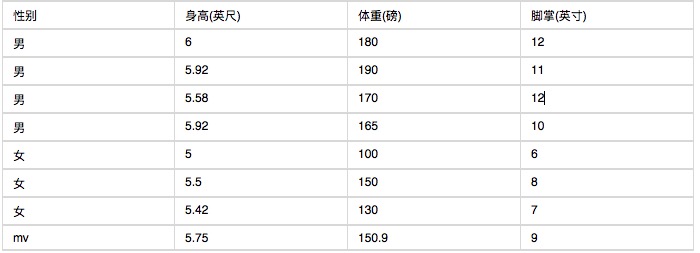
Se você sabe que uma pessoa tem 6 pés de altura, 130 libras e 8 polegadas de palmas das mãos, pergunte se ela é homem ou mulher. Calcule o valor da seguinte fórmula com base no classificador básio simplório:

P (altura e sexo) x P (peso e sexo) x P (pés e sexo) x P (sexo)

A dificuldade aqui é que, uma vez que a altura, o peso e as palmas das mãos são variáveis contínuas, não é possível calcular a probabilidade usando o método das variáveis isoladas. E, como a amostra é muito pequena, não é possível dividir o cálculo em intervalos. O que fazer?

Com esses dados, é possível calcular a classificação de gênero.

P (altura = 6 anos de idade) x P (peso = 130 anos de idade) x P (palma = 8 anos de idade) x P (homem)

= 6.1984 x e-9

P (altura = 6 anos de idade) x P (peso = 130 anos de idade) x P (palmas = 8 anos de idade) x P (mulher)

= 5.3778 x e-4

Como pode ser visto, as mulheres são quase 10.000 vezes mais propensas do que os homens a ser diagnosticadas como mulheres.

O número público do WeChat de Deng Xiaoping