Modelo de Markov Oculto

• ### Conhecer

Hoje vamos falar sobre a aplicação simples do HMM em ações.

O modelo de Markov oculto, que parece muito sofisticado e não se sabe ao certo o que é, então vamos dar um passo atrás e olhar para a cadeia de Markov.

A cadeia de Markov, nomeada em homenagem a Andrei Markov (A.A. Markov, 1856-1922), é um processo aleatório de eventos dissociados que possuem a natureza de Markov em matemática. Em um dado contexto de conhecimento ou informação atual, o passado (isto é, o estado histórico anterior ao presente) é irrelevante para prever o futuro (isto é, o estado futuro posterior ao presente).

O processo, em que cada estado de transferência depende apenas dos n estados anteriores, é conhecido como modelo de 1 n graus, onde n é o número de estados de transferência afetados. O processo de Markov mais simples é o processo de um grau, em que cada estado de transferência depende apenas do estado anterior.

• ### Exemplo dois.

A expressão matemática é a seguinte:

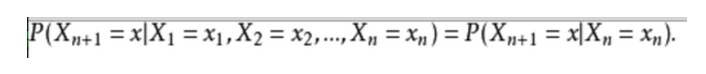
Para dar um exemplo do dia-a-dia, nós queremos prever o que acontecerá no futuro com base no estado atual do tempo. Uma maneira de fazer isso é assumir que cada estado do modelo depende apenas do estado anterior, a hipótese de Markov, que simplifica muito o problema.

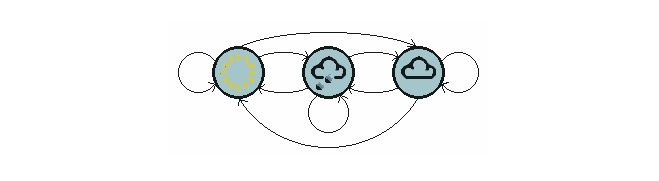
O gráfico acima mostra um modelo de transferência climática.

Observe que um processo de uma etapa contendo N estados tem N2 mudanças de estado. A probabilidade de cada mudança é chamada de probabilidade de mudança de estado, ou seja, a probabilidade de mudança de um estado para outro. Todas essas N2 probabilidades podem ser representadas por uma matriz de mudança de estado, a matriz de mudança de estado do exemplo do tempo acima é a seguinte:

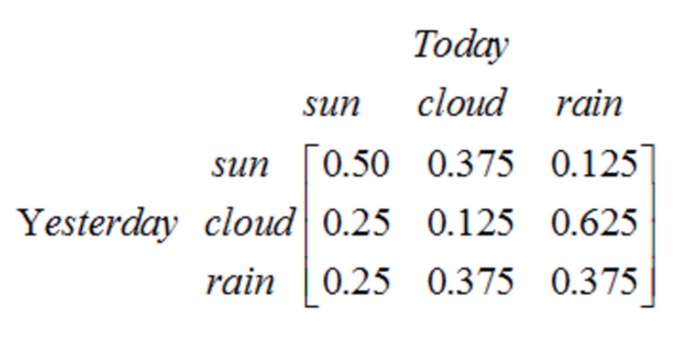
Esta matriz diz que, se ontem foi nublado, há uma probabilidade de 25% de que hoje seja um dia de sol, uma probabilidade de 12.5% de que seja nublado, e uma probabilidade de 62.5% de que chova. Obviamente, a soma de cada linha da matriz é 1.

Para inicializar um sistema como esse, precisamos de um vetor de probabilidade inicial:

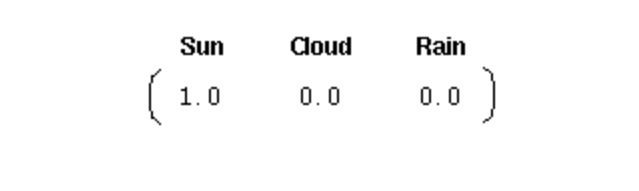
Este vetor indica que o primeiro dia foi um dia de sol claro. Aqui, definimos as três partes seguintes para o processo de Markov do primeiro grau acima:

Estado: Sol, nuvens e chuva.

Vector inicial: define a probabilidade do estado do sistema quando o tempo é zero.

Matriz de transferência de estado: a probabilidade de transferência de cada tipo de clima. Todos os sistemas que podem ser descritos dessa forma são um processo de Markov.

No entanto, o que fazer quando o processo de Markov não é suficientemente forte? Em alguns casos, o processo de Markov não é suficiente para descrever o padrão que queremos encontrar.

Por exemplo, no nosso mercado de ações, se apenas observarmos o mercado, só poderemos saber informações sobre o preço, volume de transação e outras informações do dia, mas não saberemos qual o estado atual do mercado de ações (bull market, bear market, oscilação, rebote, etc.), neste caso, temos dois conjuntos de estados, um conjunto de estados observáveis (preço de transação do mercado de ações, etc.) e um conjunto de estados ocultos (estado do mercado de ações). Esperamos encontrar um algoritmo que possa prever o estado do mercado de ações com base no preço de transação do mercado de ações e na hipótese de Markov.

Nesses casos acima, a sequência de estados observáveis e a sequência de estados ocultos estão associados à probabilidade. Assim, podemos modelar este tipo de processo como um processo de Markov oculto e um conjunto de estados observáveis associados à probabilidade desse processo de Markov oculto, o modelo de Markov oculto.

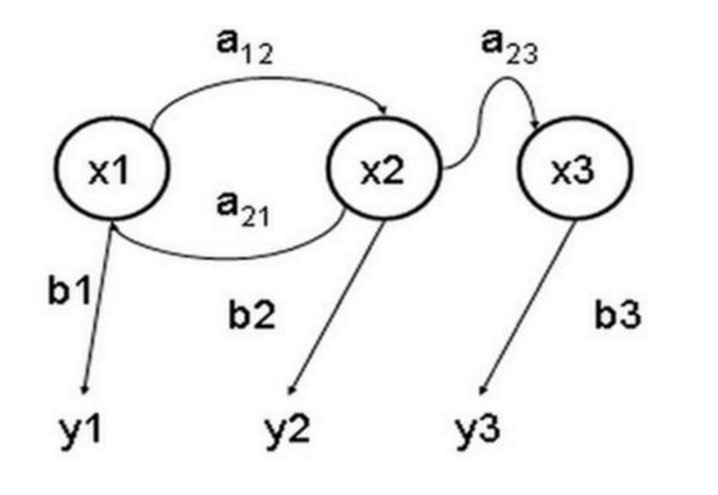
O modelo de Markov oculto é um modelo estatístico usado para descrever um processo de Markov que contém parâmetros ocultos e desconhecidos. A dificuldade consiste em identificar os parâmetros ocultos do processo a partir dos parâmetros observáveis e, em seguida, usar esses parâmetros para uma análise mais aprofundada. O gráfico a seguir é um gráfico de transferência de estado do modelo de Markov oculto em três estados, onde x representa o estado oculto, y representa a saída observável, a representa a probabilidade de conversão de estado e b representa a probabilidade de saída.

Para ilustrar com o exemplo de um cone, suponha que eu tenho três cone diferentes na mão. O primeiro cone é o cone comum que conhecemos (chamemos este cone de D6), com 6 faces, e a probabilidade de ocorrência de cada uma das faces é ¹⁄₆. O segundo cone é um quadrilateral (chamemos este cone de D4), e a probabilidade de ocorrência de cada face é ¹⁄₄. O terceiro cone tem oito faces (chamemos este cone de D8), e a probabilidade de ocorrência de cada uma das faces é ¹⁄₈.

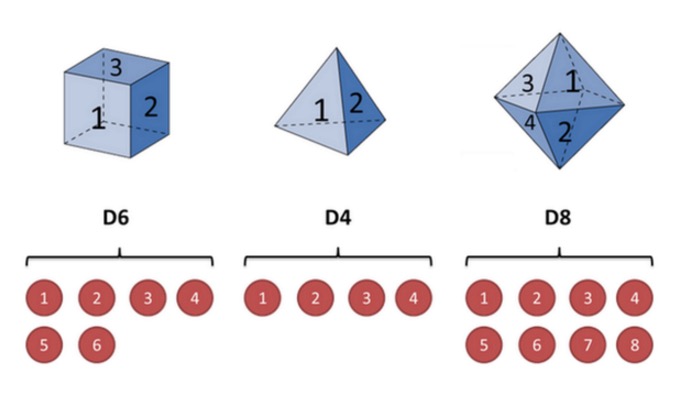
Suponhamos que começamos a escolher uma das três caixas, e a probabilidade de escolher cada uma delas é de ¹⁄₃. Então, nós escolhemos uma caixinha, e temos um número, um de 1, 2, 3, 4, 5, 6, 7, 8.

Esse número é chamado de cadeia de estados visíveis. Mas no modelo de Markov oculto, temos não apenas essa cadeia de estados visíveis, mas também uma cadeia de estados ocultos. Neste exemplo, a cadeia de estados ocultos é a sequência de pilas que você usa. Por exemplo, a cadeia de estados ocultos pode ser: D4 D6 D8 D6 D4 D8 D6 D6 D4

Em geral, a cadeia de Markov mencionada no HMM é uma cadeia de estados ocultos, pois existe uma probabilidade de conversão entre os estados ocultos (o ângulo). No nosso exemplo, o próximo estado de D6 é D4, D6, D8 tem uma probabilidade de 1 / 3. O próximo estado de D4, D8, D4, D6, D8 também tem uma probabilidade de conversão de 1 / 3.

Da mesma forma, embora não haja uma probabilidade de conversão entre os estados visíveis, há uma probabilidade entre os estados ocultos e os estados visíveis chamada de probabilidade de saída. No nosso exemplo, a probabilidade de saída de um dado de seis faces (D6) é ¹⁄₆. A probabilidade de saída de um dado de 2, 3, 4, 5, 6 também é ¹⁄₆.

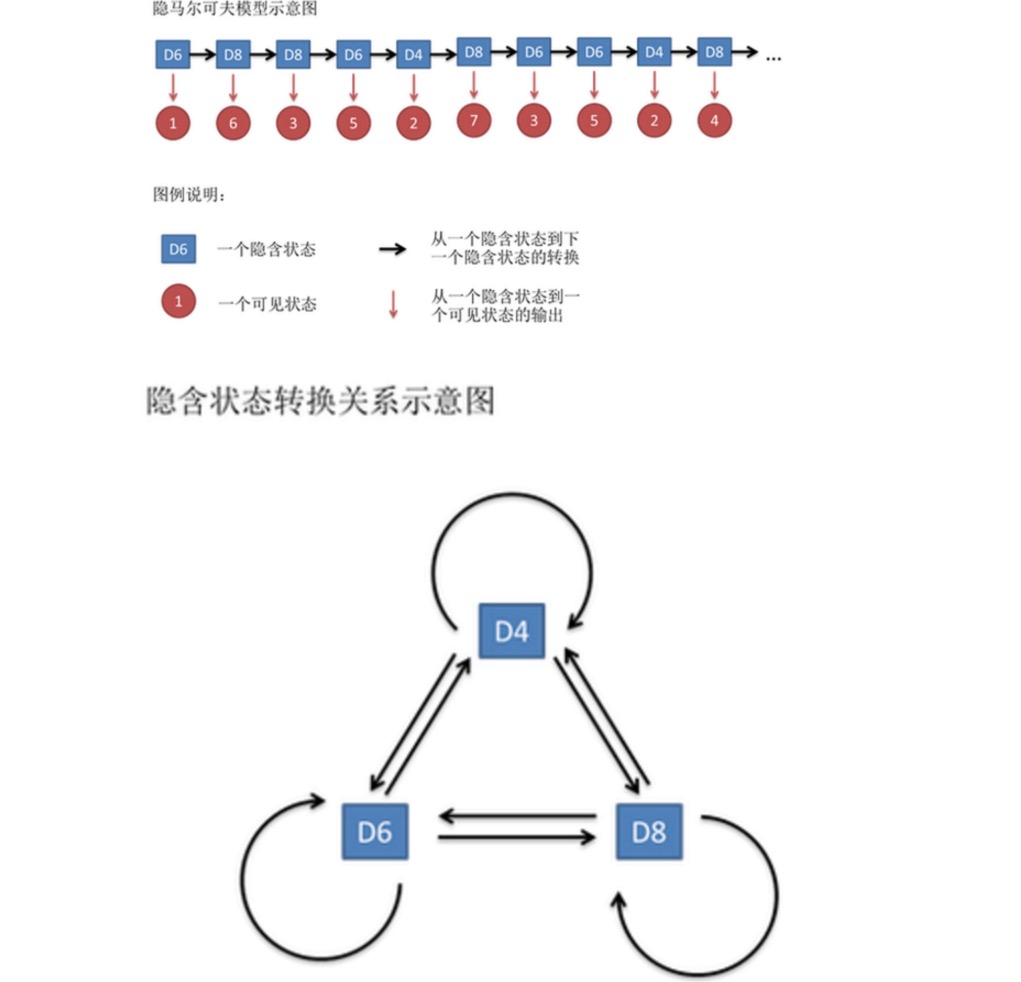
Na verdade, para o HMM, é bastante fácil fazer simulações se você souber antecipadamente a probabilidade de conversão entre todos os estados ocultos e a probabilidade de saída entre todos os estados ocultos e todos os estados visíveis. Mas quando se aplica o modelo HMM, muitas vezes falta parte da informação. Às vezes, você sabe quantos tipos de alfinetes existem e o que é cada tipo de alfinete, mas não sabe a sequência de alfinetes extraída; às vezes você apenas vê o resultado de muitos alfinetes e não sabe o resto.

Algoritmos relacionados ao modelo HMM são divididos em três categorias, cada uma com três tipos de problemas:

• Sabendo quantos tipos de conchas existem (número de estados implicados), o que cada tipo de concha é (probabilidade de conversão), e de acordo com o resultado da concha (cadeia de estados visíveis), eu gostaria de saber qual tipo de concha é que é extraído a cada vez (cadeia de estados implicados).

• Eu também quero saber quantos tipos de conjuntos existem ((número de estados implícitos), o que é cada tipo de conjuntos ((probabilidade de conversão), de acordo com o resultado do conjuntos ((cadeia de estados visíveis), eu gostaria de saber a probabilidade de extrair este resultado.

• Sabendo que há vários tipos de anéis (número de estados implícitos), não sabendo o que cada um deles é (probabilidade de conversão), observando o resultado de muitos tipos de anéis (cadeia de estados visíveis), eu gostaria de inferir o que cada um deles é (probabilidade de conversão).

  Se queremos resolver o problema do mercado de ações acima, precisamos resolver o problema 1 e o problema 3, e no próximo artigo veremos como isso pode ser feito.

Transcrito de um artigo do Moneycode