Compreensão intuitiva da cointegração

Introdução: O objetivo deste artigo é apresentar o conceito de integração de forma intuitiva, ajudando a entender o seu significado básico, a motivação que o conceito apresenta e os simples cenários de aplicação.

• Currículo de integração

Aqui, apenas quero apontar que a definição intuitiva de integração não envolve definições rigorosas de símbolos matemáticos e deduções de fórmulas rigorosas.

Se você estiver interessado, consulte: Wikipedia Cointegration.

Por que ser equilibrado/coerente

O blogueiro também escreveu sobre o tema: “A integração é uma questão de estabilidade”.

Simplificando, estabilidade é a propriedade de uma sequência que se mantém estável ao longo do tempo, e é uma propriedade que gostamos muito de fazer previsões analíticas de dados. Se um conjunto de dados de sequência de tempo é estável, isso significa que suas médias e diferenças permanecem inalteradas, para que possamos usar com facilidade algumas técnicas estatísticas na sequência. Vamos primeiro ver um exemplo para entender o que as sequências estáveis e não estáveis são intuitivamente.

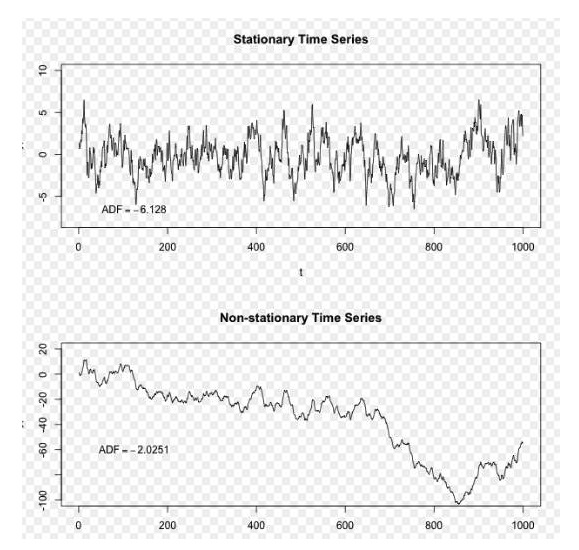
Imagem: Wikipedia

Na figura acima, a sequência em cima é uma sequência estável, e podemos ver que ela está sempre flutuando em torno de uma média de longo prazo, e a sequência em baixo é uma sequência não estável, e podemos ver que sua média de longo prazo é variável.

Para dar um exemplo de aplicação, se a sequência de preços de um determinado ativo (ou a diferença de preços entre duas sequências) for estável, então, quando ele se desvia de seu valor médio, pode-se esperar que o preço volte a esse valor médio em algum momento futuro. Podemos usar essa propriedade para investir e lucrar. Suponha que o valor médio a longo prazo de uma ação é de US \( 9, e o valor atual é de US \) 8. Se, após a verificação, considerarmos que a sequência histórica desta ação tem a natureza estável, e assumirmos que essa estabilidade pode ser mantida, podemos comprar essa ação e esperar que seu preço volte a US \( 9 no futuro, obtendo assim um lucro de US \) 1.

A sequência de preços das ações é estabilizadora:

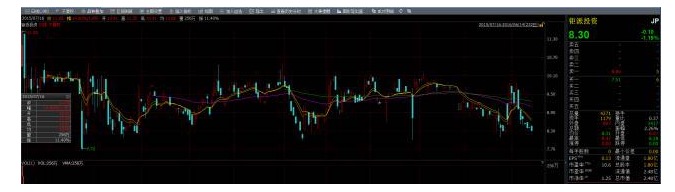
A estabilidade é muito útil, mas na realidade, a maioria das ações são não estáveis, então será que ainda podemos aproveitar a propriedade de estabilidade para lucrar? A resposta é sim, então a cointegração entra em jogo! Se dois conjuntos de sequências não são estáveis, mas sua combinação linear pode obter uma sequência estável, então dizemos que os dois conjuntos de dados de sequência de tempo têm a propriedade de cointegração, e também podemos usar a propriedade estatística para a sequência da combinação.

Por exemplo, se dois conjuntos de dados de sequência de tempo são iguais, podemos investir com lucro com base na estabilidade do diferencial: quando o preço de duas ações é muito diferente, de acordo com a estabilidade, esperamos que o diferencial de preço se converja, então compramos ações de baixo preço, vendemos ações de alto preço e esperamos que o preço retorne para obter lucro.

É a origem do comércio de pares.

• Estabilidade e métodos de teste

Estritamente falando, a estabilidade pode ser dividida em estabilidade estritamente estacionária e estabilidade fraca. Estabilidade estritamente estacionária significa que uma sequência sempre possui uma função de distribuição invariável, enquanto estabilidade fraca significa que a sequência possui uma constante de quantidade descritiva. Todas as sequências de estabilidade forte satisfazem a propriedade de estabilidade fraca, mas o contrário não é válido.

Um exemplo de aplicação

Em primeiro lugar, é importante ressaltar que as relações de convergência não são relações de correlação. Nós construímos artificialmente dois conjuntos de dados, e assim podemos visualizar as relações de convergência. import numpy as np import pandas as pd import seaborn import statsmodels import matplotlib.pyplot as plt from statsmodels.tsa.stattools import coint

Construção de dados

Primeiro, construímos dois conjuntos de dados, cada um com a duração de 100 ⋅ o primeiro conjunto de dados é 100 mais um elemento de tendência descendente e mais uma distribuição normal padrão ⋅ o segundo conjunto de dados baseia-se no primeiro conjunto de dados e acrescenta 30 e mais uma distribuição normal padrão adicional ⋅ há

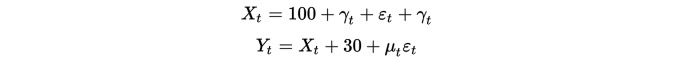
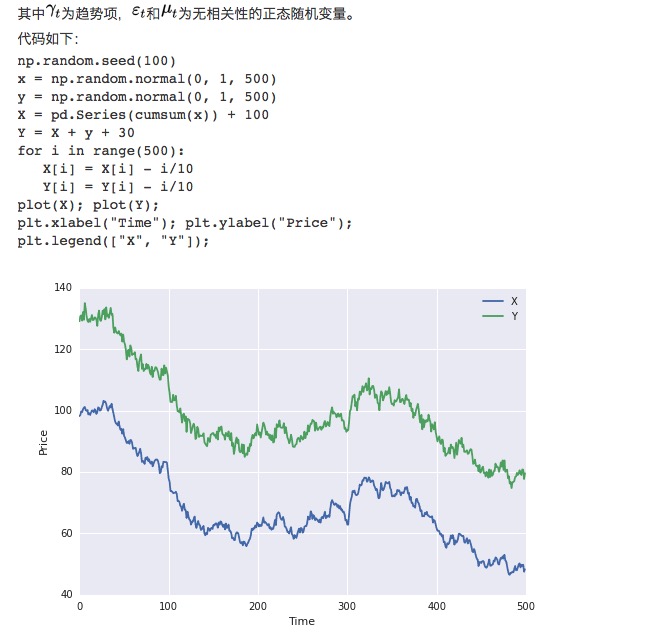
Obviamente, ambos os conjuntos de dados são iniguais, pois os valores médios variam com o tempo. Mas os dois conjuntos de dados são coerentes, pois suas sequências diferenciais são estáveis:

plot(Y-X); plt.axhline((Y-X).mean(),color=“red”, linestyle=“–”); plt.xlabel(“Time”); plt.ylabel(“Price”); plt.legend([“Y-X”, “Mean”]);

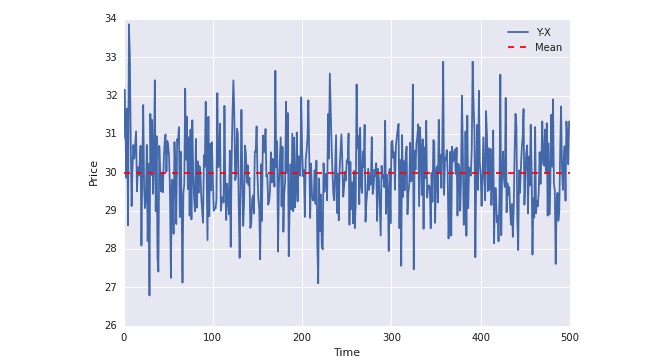
No gráfico acima, pode-se ver que a linha azul tem vindo a flutuar em torno da média. A média não muda com o tempo (na verdade, quase não muda com o tempo).

• Conclusão

A integração é muito mais complexa se for explicada apenas do ponto de vista da matemática, e será abordada em uma aula de quantificação posterior. Nós apenas fizemos uma breve introdução a nível de compreensão (nível-0) com o objetivo de que todos possam melhor combinar a integração com aplicações reais.

A partir daí, a quantidade de pessoas que estão sendo levadas para a sala de aula é reduzida para a quantidade de pessoas que estão sendo levadas para a sala.