A curva de Van Moerv e os deuses

Na edição anterior, foi dito que, quando Jacob Bernoulli morreu, ainda não havia publicado o seu livro de especulações sobre a teoria da probabilidade. A tarefa de organizar o seu manuscrito foi entregue a seu sobrinho, Nicholas Bernoulli II (o gênio da madrugada). O nome de Abraham de Moivre é traduzido em muitos lugares como “Moivre”, mas depois de ver o retrato dele, eu não sou muito favorável a essa tradução. O convite poderia ter alcançado um período de glória no mundo dos mortos, mas Moivre recusou. E a razão pela qual ele recusou foi porque ele sentiu que não tinha força suficiente.

• - O que é? Na verdade, Montmorency era apenas um adolescente mais novo que Jacob Bernoulli, e sua vida inteira poderia ser descrita em um romance, que era O Mundo Miserável. Naquela época, a França era um país com um clima católico fanático, e Montmorency era um protestante. Mais tarde, o rei francês Luís XIV promulgou um decreto que declarava os protestantes nacionais cidadãos inferiores, e os filhos tinham que se converter ao protestantismo.

Mas, mesmo assim, vamos fazer um grito de guerra aqui: Que o Bom Morpho seja imortal! Em 1711, o Bom Morpho publicou um conto sobre a medida da sorte, o que, se tivesse sido publicado na época, teria sido encoberto com a recomendação de Newton: “Pergunte ao Sr. Bom Morpho, ele sabe mais sobre isso do que eu”.

Mas, infelizmente, na época não havia, então o Tommour não conseguiu ganhar muito dinheiro com o imposto.

Você deve se lembrar do nosso problema no artigo anterior (Risky Little Story 3): Coronel Bernoulli), para 5.000 pedras de um barril, nós podemos fazer 25.500 arranhões para estimar a proporção do total de pedras de um barril. Mas você também deve descobrir que 25.500 arranhões repetidos é muito, é melhor derramar uma pedra em um número.

Usando métodos de cálculo e triângulo de Pascal, ele adotou um método de amostragem por agrupamento. Ele supõe que, a cada vez, 100 pedras de alumínio são retiradas de uma caixa, as proporções das pedras de alumínio preto e branco são registradas e as pedras são colocadas de volta, e a mesma extração é feita novamente. Com esse método, ele pode dizer antecipadamente o desvio aproximado das proporções registradas em relação às proporções reais e como essas proporções são distribuídas em torno de suas médias.

Sim, essa é a distribuição normal que todos conhecemos. A curva da distribuição normal é como uma curva em forma de sino, com a maioria dos valores observados agrupados no meio, perto da média de todos os valores observados, e depois inclinada simetricamente para os dois lados da média, e o número de valores observados em ambos os lados da média é igual.

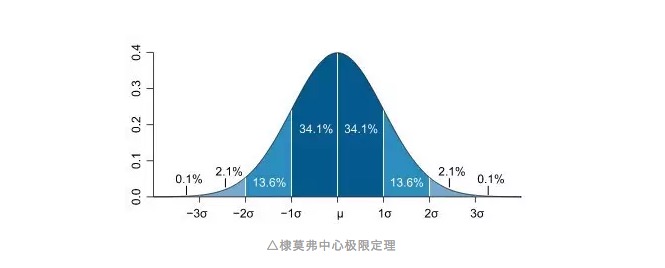
Assim, podemos introduzir o conceito de diferença padrão, que já foi mencionado em outros artigos da publicação: Por que diferença padrão? Medidas de risco aos olhos de Deus. A diferença padrão descreve o grau de desvio do valor observado em relação à média, ou entendemos como uma unidade de desvio em relação à média.

Como um religioso devoto, Dunmoor considerava a curva de relógio como um produto de Deus. Em sua opinião, com tal medida podemos vencer a incerteza e, em seguida, conquistar todos os riscos, pois a curva descreve todos os fenômenos possíveis e suas probabilidades, talvez por causa do acaso que produziria os chamados desvios, mas com o passar do tempo, esses desvios não afetariam mais a lei que resumimos.

Para explicar a forma como todos gostam e gostam de interpretar o que o Tom Morrow disse, é que a decepção é o número de telefone que não funciona de vez em quando, tente mais vezes e sempre responde. Há também um tema clássico do ensino médio (por que eu sempre uso o tema do ensino médio) sobre a taxa de aprovação do produto. Se, para um grupo de produtos, os padrões do setor consideram que a taxa de resíduos não é superior a 0,1%, isso significa que nós selecionamos aleatoriamente 10.000 produtos, dos quais, se a taxa de resíduos não for superior a 10, eles são aprovados.

Mas, na maioria das vezes, essa pergunta não faz sentido para nós. Porque na verdade, talvez não saibamos qual é a taxa média de desperdício de um produto, e se a taxa média de desperdício for maior do que o padrão de detecção, então qual é a probabilidade de um lote de produtos passarem o teste? Se 20 mil produtos forem testados, os resultados de 10 mil produtos podem ser obtidos diretamente?

Transcrição feita pela China Quantitative Investment Association