Reflexões sobre estratégias de negociação de alta frequência (1)
 3
3
 4856
4856

O artigo discute as estratégias de negociação de alta frequência de moedas digitais, incluindo as fontes de lucros (principalmente de flutuações de mercado e descontos em taxas de câmbio), as questões de colocação de ordens e controle de posição, e o método de modelagem de volume de negociação usando a distribuição de Pareto. Além disso, os dados de transações e ordens ideais fornecidos pela Binance foram usados para backtesting, e outras questões de estratégias de negociação de alta frequência estão planejadas para serem discutidas em profundidade em artigos subsequentes.
Já escrevi dois artigos sobre negociação de alta frequência de moedas digitais. Uma introdução detalhada às estratégias de moeda digital de alta frequência, Ganhe 80 vezes em 5 dias, o poder da estratégia de alta frequência. Mas isso só pode ser considerado como compartilhamento de experiências e conversas gerais. Desta vez, planejo escrever uma série de artigos para introduzir as ideias de negociação de alta frequência desde o início. Espero ser o mais conciso e claro possível. No entanto, devido ao meu nível limitado e profundo entendimento de negociação de alta frequência, trading, este artigo é apenas um ponto de partida. Espero que os especialistas possam me corrigir.
Fontes de lucro de alta frequência
Como mencionado em artigos anteriores, estratégias de alta frequência são particularmente adequadas para mercados com altos e baixos extremamente voláteis. Examine as mudanças de preço de um produto comercial em um curto período de tempo, que consiste em tendências e flutuações gerais. Se pudermos prever com precisão as mudanças nas tendências, certamente podemos ganhar dinheiro, mas isso também é o mais difícil. Este artigo apresenta principalmente estratégias de alta frequência e não envolverá essa questão. Em um mercado volátil, se a estratégia de colocar ordens para cima e para baixo for executada com frequência suficiente e a margem de lucro for grande o suficiente, ela pode cobrir as possíveis perdas causadas pela tendência, de modo que você pode lucrar sem prever o mercado. Atualmente, todas as transações de maker em exchanges recebem descontos em taxas de transação, que também são um componente do lucro. Quanto mais intensa a competição, maior deve ser a proporção de descontos.
Problema a ser resolvido
A estratégia coloca ordens de compra e ordens de venda ao mesmo tempo. A primeira questão é onde colocar as ordens. Quanto mais próxima a ordem estiver do mercado, maior a probabilidade de uma transação. No entanto, em um mercado volátil, o preço instantâneo da transação pode estar muito longe do mercado. Se a ordem for colocada muito perto, você não conseguirá obter lucro suficiente. A probabilidade de execução de ordens colocadas muito distantes é baixa. Este é um problema que precisa ser otimizado.
Controle sua posição. Para controlar os riscos, a estratégia não pode acumular muitas posições por muito tempo. Isso pode ser resolvido controlando a distância do pedido, a quantidade do pedido, o limite de posição total, etc.
Para atingir os objetivos acima, é necessário modelar e estimar a probabilidade de transação, lucro da transação, estimativa de mercado e outros aspectos. Existem muitos artigos e papers nesta área, que podem ser encontrados com palavras-chave como High-Frequency Trading , Livro de ordens, etc. Há muitas recomendações online, mas não vou entrar em detalhes aqui. Além disso, é melhor estabelecer um sistema de backtesting confiável e rápido. Embora estratégias de alta frequência possam ser facilmente verificadas por meio de negociações reais para verificar sua eficácia, o backtesting ainda pode fornecer mais ideias e reduzir o custo de tentativa e erro.
Dados requeridos
A Binance fornece dados de transação por transação e de melhor ordemdownloadOs dados profundos precisam ser baixados usando a API na lista de permissões, ou você mesmo pode coletá-los. Para fins de backtesting, você pode usar apenas os dados de transação coletados. Este artigo usa os dados de HOOKUSDT-aggTrades-2023-01-27 como exemplo.
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
As colunas de transação são as seguintes:
- agg_trade_id: o id da ordem de transação agregada,
- Preço: preço da transação
- Quantidade: O número de transações
- first_trade_id: Pode haver várias transações na coleção ao mesmo tempo, apenas um dado é contado, este é o id da primeira transação
- last_trade_id: o id da última transação
- transact_time: tempo de transação
- is_buyer_maker: direção da transação, Verdadeiro significa que a ordem de compra é negociada pelo criador e a ordem de venda é negociada pelo tomador
Pode-se observar que houve 660.000 dados de transações naquele dia, e as transações foram muito ativas. O csv será anexado na seção de comentários.
trades = pd.read_csv('COMPUSDT-aggTrades-2023-07-02.csv')
trades
664475 rows × 7 columns
| agg_trade_id | price | quantity | first_trade_id | last_trade_id | transact_time | is_buyer_maker |
|---|---|---|---|---|---|---|
| 120719552 | 52.42 | 22.087 | 207862988 | 207862990 | 1688256004603 | False |
| 120719553 | 52.41 | 29.314 | 207862991 | 207863002 | 1688256004623 | True |
| 120719554 | 52.42 | 0.945 | 207863003 | 207863003 | 1688256004678 | False |
| 120719555 | 52.41 | 13.534 | 207863004 | 207863006 | 1688256004680 | True |
| … | … | … | … | … | … | … |
| 121384024 | 68.29 | 10.065 | 210364899 | 210364905 | 1688342399863 | False |
| 121384025 | 68.30 | 7.078 | 210364906 | 210364908 | 1688342399948 | False |
| 121384026 | 68.29 | 7.622 | 210364909 | 210364911 | 1688342399979 | True |
Modelagem de volume de transação única
Primeiro, processe os dados e divida as negociações originais em grupo de transações ativas de ordem de compra e grupo de transações ativas de ordem de venda. Além disso, os dados de transação agregados originais são um pedaço de dados ao mesmo tempo, no mesmo preço e na mesma direção. Pode haver uma ordem de compra ativa com um volume de 100. Se for dividido em várias transações com diferentes preços, como 60 e 40, Dois dados serão gerados, afetando a estimativa do volume de ordens de compra. Portanto, é necessário agregar novamente com base em transact_time. Após a agregação, a quantidade de dados foi reduzida em 140.000 registros.
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
sell_trades = trades[trades['is_buyer_maker']==True].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
sell_trades = sell_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
sell_trades['interval']=sell_trades['transact_time'] - sell_trades['transact_time'].shift()
print(trades.shape[0] - (buy_trades.shape[0]+sell_trades.shape[0]))
146181
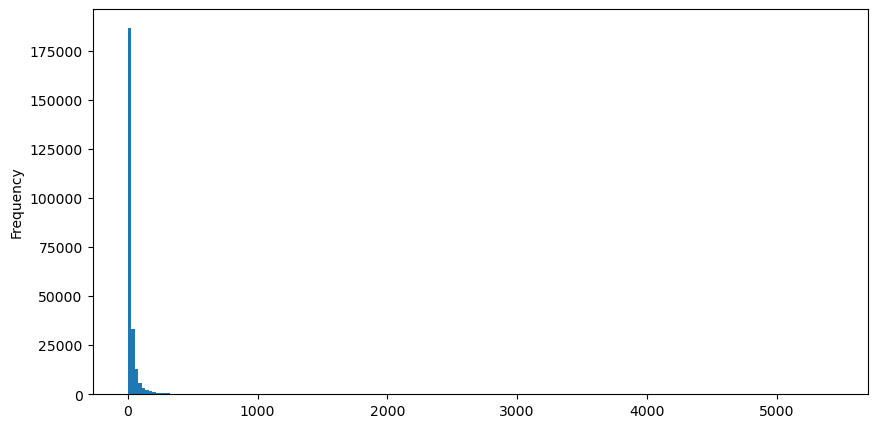
Tomando ordens de compra como exemplo, primeiro desenhe um histograma. Você pode ver que o efeito de cauda longa é muito óbvio. A maioria dos dados está concentrada na extrema esquerda, mas também há um pequeno número de grandes transações distribuídas na cauda .
buy_trades['quantity'].plot.hist(bins=200,figsize=(10, 5));
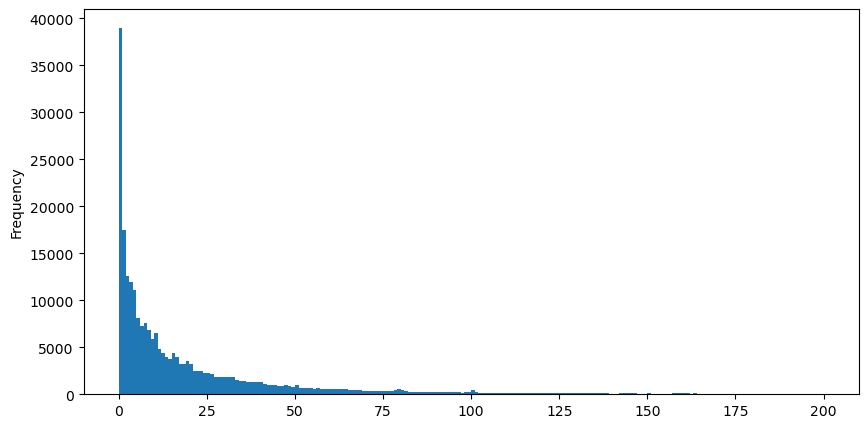
Para a conveniência da observação, cortamos a cauda e observamos. Podemos ver que quanto maior o volume de negociação, menor a frequência de ocorrência e mais rápida a tendência de queda.
buy_trades['quantity'][buy_trades['quantity']<200].plot.hist(bins=200,figsize=(10, 5));
Existem muitos estudos sobre a distribuição da satisfação com o volume. Sua distribuição de lei de potência também é chamada de distribuição de Pareto, que é uma forma comum de distribuição de probabilidade em física estatística e ciências sociais. Em uma distribuição de lei de potência, a probabilidade de um evento de um certo tamanho (ou frequência) é proporcional a algum expoente negativo do tamanho desse evento. A principal característica dessa forma de distribuição é que eventos grandes (ou seja, aqueles distantes da média) ocorrem com mais frequência do que seria esperado em muitas outras distribuições. Esta é a característica da distribuição do volume de negociação. A forma da distribuição de Pareto é: P(x) = Cx^(-α). O que se segue demonstrará isso.
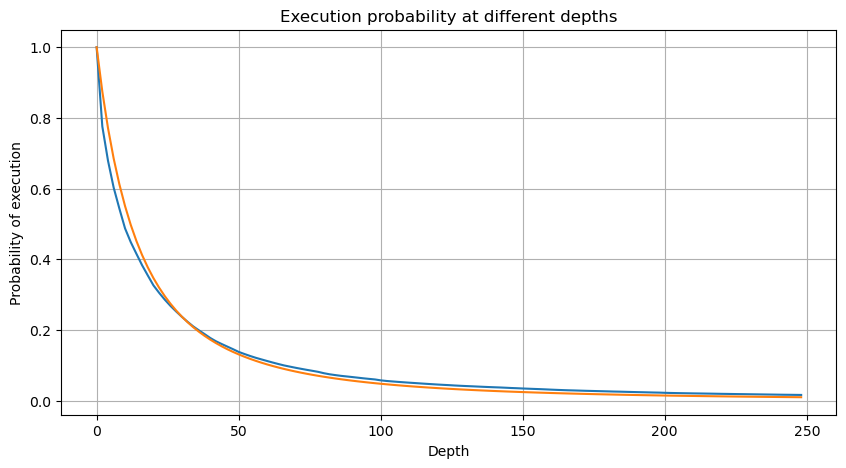
A figura abaixo mostra a probabilidade de que o volume de negociação seja maior que um certo valor. A linha azul é a probabilidade real, e a linha laranja é a probabilidade simulada. Não se preocupe com os parâmetros específicos aqui. Você pode ver que isso acontece satisfazem a distribuição de Pareto. Como a probabilidade de o volume do pedido ser maior que 0 é 1, e para atender aos requisitos de padronização, a equação de distribuição deve ser a seguinte:
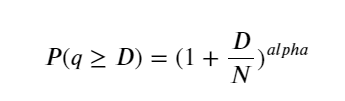
Onde N é o parâmetro padronizado. Aqui selecionamos o volume médio M e alfa -2,06. A estimativa específica de alfa pode ser calculada calculando inversamente o valor de P quando D=N. Especificamente: alfa = log(P(d>M))/log(2) . A escolha de pontos diferentes resultará em valores alfa ligeiramente diferentes.
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
alpha = np.log(np.mean(buy_trades['quantity'] > mean_quantity))/np.log(2)
mean_quantity = buy_trades['quantity'].mean()
probabilities_s = np.array([(1+depth/mean_quantity)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
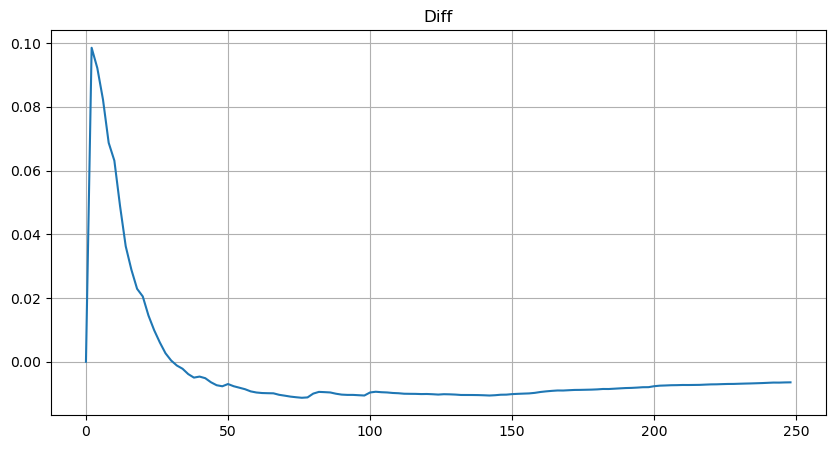
Mas essa estimativa só parece. Na figura acima, plotamos a diferença entre o valor simulado e o valor real. Quando o volume de negociação é pequeno, o desvio é grande, até próximo de 10%. A probabilidade de um ponto pode ser mais precisa selecionando pontos diferentes durante a estimativa de parâmetros, mas isso não resolve o problema do desvio. Isso é determinado pela diferença entre a distribuição de lei de potência e a distribuição real. Para obter resultados mais precisos, a equação da distribuição de lei de potência precisa ser corrigida. Não vou entrar em detalhes sobre o processo específico, mas tive um lampejo de inspiração e descobri que deveria ser assim:
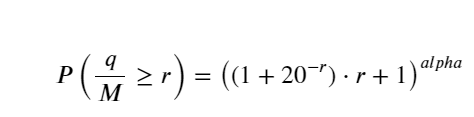
Para simplificar, r = q/M é usado aqui para representar o volume de negociação padronizado. Os parâmetros podem ser estimados da mesma forma que acima. A figura abaixo mostra que o desvio máximo após a correção não excede 2%. Teoricamente, a correção pode ser continuada, mas essa precisão é suficiente.
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([(((1+20**(-depth/mean))*depth+mean)/mean)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
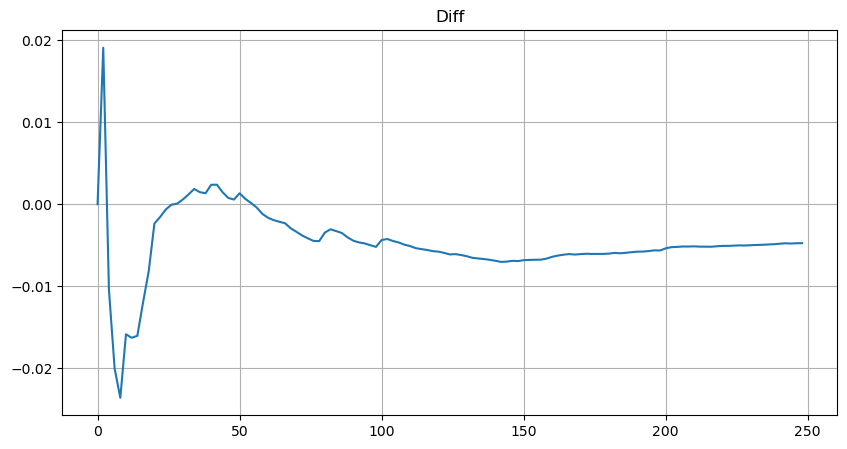
Com a equação estimada para a distribuição de volume, observe que a probabilidade da equação não é a probabilidade verdadeira, mas uma probabilidade condicional. Neste ponto podemos responder a esta pergunta: se a próxima ordem ocorrer, qual é a probabilidade de que esta ordem seja maior que um determinado valor? Em outras palavras, qual é a probabilidade de execução de ordens de diferentes profundidades (situação ideal, não tão rigorosa, em teoria o livro de ordens tem novas ordens e cancelamentos, além de filas na mesma profundidade).
O artigo está quase pronto aqui, e ainda há muitas perguntas que precisam ser respondidas. A série de artigos a seguir tentará fornecer respostas.