Reflexões sobre estratégias de negociação de alta frequência (3)
 0
0
 2664
2664

No artigo anterior, apresentei como modelar o volume acumulado de negociação e analisei brevemente o fenômeno do choque de preços. Este artigo continuará analisando dados de ordens de negociação. Nos últimos dois dias, a YGG lançou contratos baseados na Binance U, e o preço flutuou muito, e o volume de negociação até excedeu o BTC em um ponto. Vamos analisar isso hoje.
Intervalo de tempo do pedido
Em geral, assume-se que o momento em que os pedidos chegam segue um processo de Poisson. Aqui está um artigo que apresentaProcesso de Poisson . Demonstrarei isso abaixo.
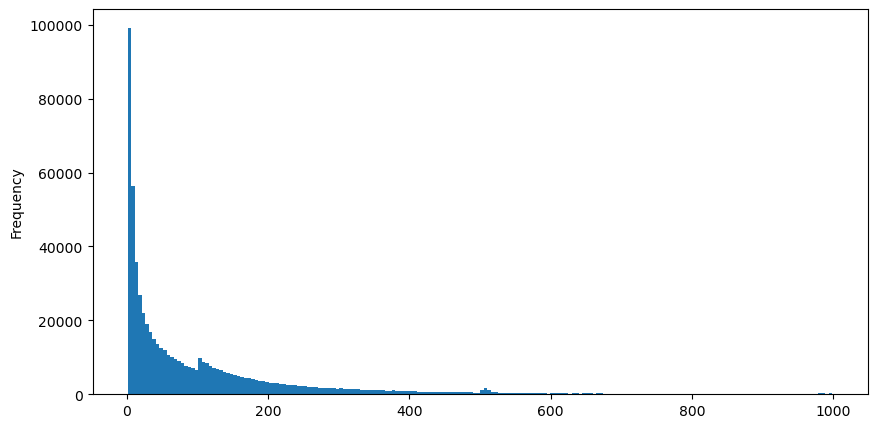
Baixe o aggTrades em 5 de agosto, há 1.931.193 negociações no total, o que é bastante exagerado. Primeiro, vamos dar uma olhada na distribuição de ordens de compra. Podemos ver que há um pico local irregular em torno de 100 ms e 500 ms. Isso deve ser causado pelas ordens programadas colocadas pelo robô confiado pelo Iceberg. Isso também pode ser um das razões pelas quais as condições de mercado naquele dia eram incomuns.
A função de massa de probabilidade (PMF) da distribuição de Poisson é dada por:
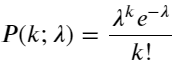
em:
- k é o número de eventos nos quais estamos interessados.
- λ é a taxa média de ocorrência de eventos por unidade de tempo (ou unidade de espaço).
- P(k; λ) é a probabilidade de exatamente k eventos ocorrerem, dada uma taxa média de ocorrência λ.
Em um processo de Poisson, os intervalos de tempo entre eventos seguem uma distribuição exponencial. A função de densidade de probabilidade (PDF) da distribuição exponencial é dada por:
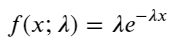
Por meio do ajuste, descobriu-se que os resultados eram bem diferentes dos resultados esperados da distribuição de Poisson. O processo de Poisson subestimou a frequência de intervalos longos e superestimou a frequência de intervalos curtos. (A distribuição de intervalo real está mais próxima da distribuição de Pareto modificada)
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
trades = pd.read_csv('YGGUSDT-aggTrades-2023-08-05.csv')
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
buy_trades.index = buy_trades['date']
buy_trades['interval'][buy_trades['interval']<1000].plot.hist(bins=200,figsize=(10, 5));
Intervals = np.array(range(0, 1000, 5))
mean_intervals = buy_trades['interval'].mean()
buy_rates = 1000/mean_intervals
probabilities = np.array([np.mean(buy_trades['interval'] > interval) for interval in Intervals])
probabilities_s = np.array([np.e**(-buy_rates*interval/1000) for interval in Intervals])
plt.figure(figsize=(10, 5))
plt.plot(Intervals, probabilities)
plt.plot(Intervals, probabilities_s)
plt.xlabel('Intervals')
plt.ylabel('Probability')
plt.grid(True)
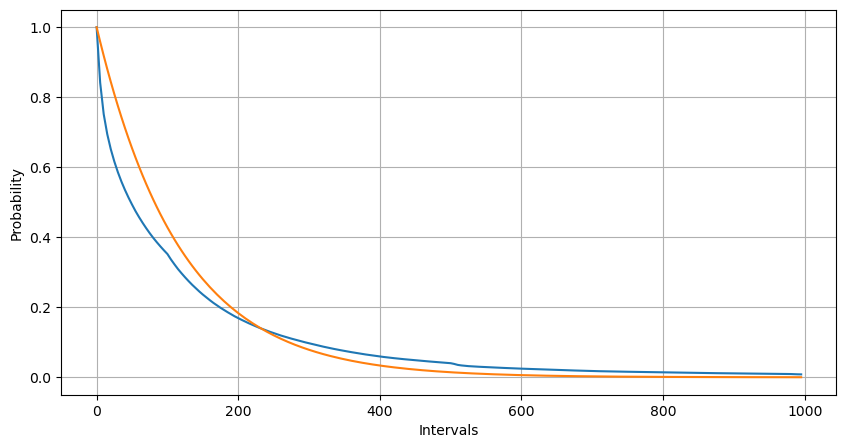
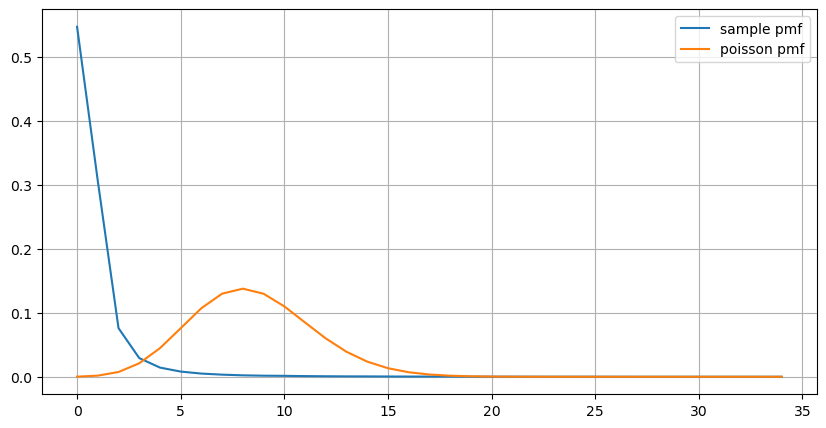
A distribuição estatística do número de ordens que ocorrem em 1 segundo e a comparação com a distribuição de Poisson também mostram uma diferença muito óbvia. A distribuição de Poisson subestima significativamente a frequência de eventos de baixa probabilidade. Possíveis causas:
- Taxa de ocorrência não constante: O processo de Poisson assume que a taxa média de eventos que ocorrem em qualquer período de tempo é constante. Se essa suposição não for válida, a distribuição dos dados se desviará de uma distribuição de Poisson.
- Interação de processos: Outra suposição básica do processo de Poisson é que os eventos são independentes uns dos outros. Se eventos do mundo real influenciam uns aos outros, sua distribuição pode se desviar da distribuição de Poisson.
Ou seja, em um ambiente real, a frequência de pedidos não é constante, precisa ser atualizada em tempo real, e incentivos ocorrerão, ou seja, mais pedidos em um tempo fixo estimularão mais pedidos. Isso torna impossível fixar um único parâmetro na estratégia.
result_df = buy_trades.resample('0.1S').agg({
'price': 'count',
'quantity': 'sum'
}).rename(columns={'price': 'order_count', 'quantity': 'quantity_sum'})
count_df = result_df['order_count'].value_counts().sort_index()[result_df['order_count'].value_counts()>20]
(count_df/count_df.sum()).plot(figsize=(10,5),grid=True,label='sample pmf');
from scipy.stats import poisson
prob_values = poisson.pmf(count_df.index, 1000/mean_intervals)
plt.plot(count_df.index, prob_values,label='poisson pmf');
plt.legend() ;
Parâmetros de atualização em tempo real
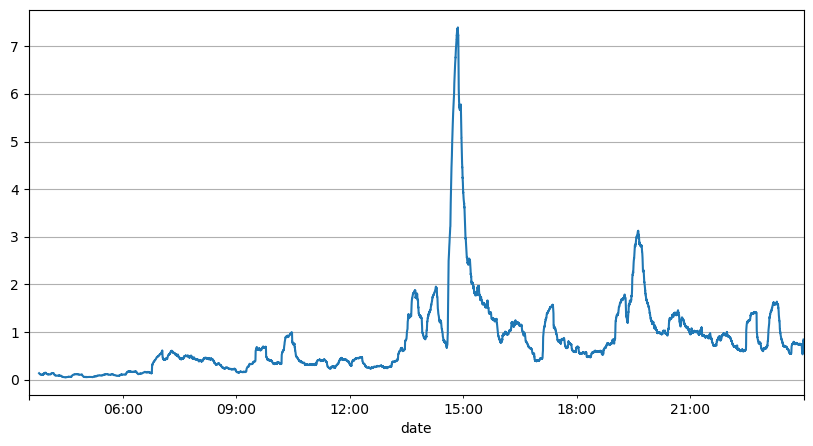
A análise anterior dos intervalos de ordens mostra que parâmetros fixos não são adequados para condições reais de mercado, e os principais parâmetros da descrição de mercado da estratégia precisam ser atualizados em tempo real. A solução mais fácil de pensar é a média móvel da janela deslizante. As duas figuras abaixo são a frequência de ordens de compra dentro de 1 segundo e a média de 1000 janelas de volume de negociação. Pode-se observar que há um fenômeno de clustering nas transações, ou seja, a frequência de ordens é significativamente maior do que o normal para um período de tempo, e o volume neste momento também aumenta de forma sincronizada. Aqui, a média anterior é usada para prever o valor do último segundo, e o erro absoluto médio do resíduo é usado para medir a qualidade da previsão.
Do gráfico, também podemos entender por que a frequência de pedidos desvia tanto da distribuição de Poisson. Embora o número médio de pedidos por segundo seja de apenas 8,5 vezes, em casos extremos o número médio de pedidos por segundo desvia muito dela.
Descobriu-se aqui que usar a média dos dois segundos anteriores para prever o erro residual é o menor e muito melhor do que o resultado da previsão da média simples.
result_df['order_count'][::10].rolling(1000).mean().plot(figsize=(10,5),grid=True);
result_df
| order_count | quantity_sum | |
|---|---|---|
| 2023-08-05 03:30:06.100 | 1 | 76.0 |
| 2023-08-05 03:30:06.200 | 0 | 0.0 |
| 2023-08-05 03:30:06.300 | 0 | 0.0 |
| 2023-08-05 03:30:06.400 | 1 | 416.0 |
| 2023-08-05 03:30:06.500 | 0 | 0.0 |
| … | … | … |
| 2023-08-05 23:59:59.500 | 3 | 9238.0 |
| 2023-08-05 23:59:59.600 | 0 | 0.0 |
| 2023-08-05 23:59:59.700 | 1 | 3981.0 |
| 2023-08-05 23:59:59.800 | 0 | 0.0 |
| 2023-08-05 23:59:59.900 | 2 | 534.0 |
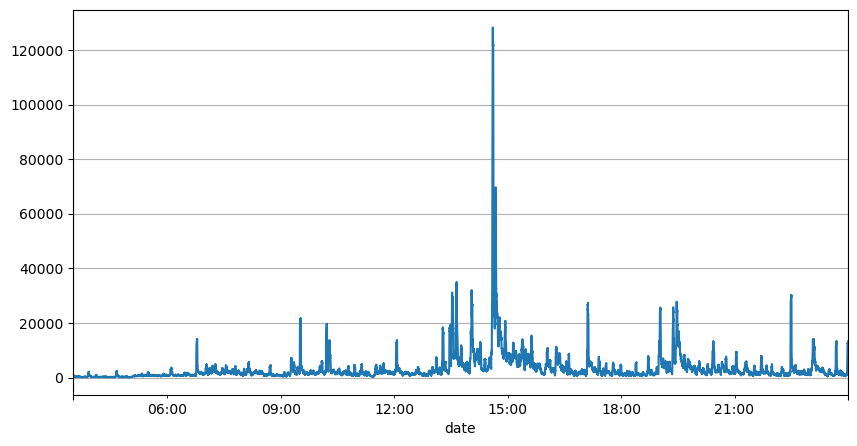
result_df['quantity_sum'].rolling(1000).mean().plot(figsize=(10,5),grid=True);
(result_df['order_count'] - result_df['mean_count'].mean()).abs().mean()
6.985628185332997
result_df['mean_count'] = result_df['order_count'].ewm(alpha=0.11, adjust=False).mean()
(result_df['order_count'] - result_df['mean_count'].shift()).abs().mean()
0.6727616961866929
result_df['mean_quantity'] = result_df['quantity_sum'].ewm(alpha=0.1, adjust=False).mean()
(result_df['quantity_sum'] - result_df['mean_quantity'].shift()).abs().mean()
4180.171479076811
Resumir
Este artigo apresenta brevemente os motivos pelos quais o intervalo de tempo do pedido se desvia do processo de Poisson, principalmente porque os parâmetros mudam ao longo do tempo. Para prever o mercado com mais precisão, a estratégia precisa fazer previsões em tempo real sobre os parâmetros básicos do mercado. Resíduos podem ser usados para medir a qualidade das previsões. O exemplo acima é o mais simples. Há muitos estudos relacionados sobre análise de séries temporais, agregação de volatilidade, etc., que podem ser melhorados ainda mais.