O artigo anterior estudou o intervalo de chegada do pedido e demonstrou por que precisamos ajustar dinamicamente os parâmetros e como avaliar a qualidade da estimativa. Este artigo se concentrará em dados aprofundados e estudará o preço médio (também chamado de preço justo, micropreço, etc.).

Dados de profundidade

A Binance fornece download de dados históricos das melhores cotações, incluindo best_bid_price: o melhor preço de oferta, ou seja, o preço máximo de oferta, best_bid_qty: o número do melhor preço de oferta, best_ask_price: o melhor preço de venda, best_ask_qty: o número do melhor preço de venda , transaction_time: registro de data e hora. Esses dados não incluem ordens pendentes de segundo nível e mais profundas. A situação de mercado analisada aqui é a YGG em 7 de agosto. As flutuações do mercado naquele dia foram muito drásticas, e a quantidade de dados atingiu mais de 9 milhões.

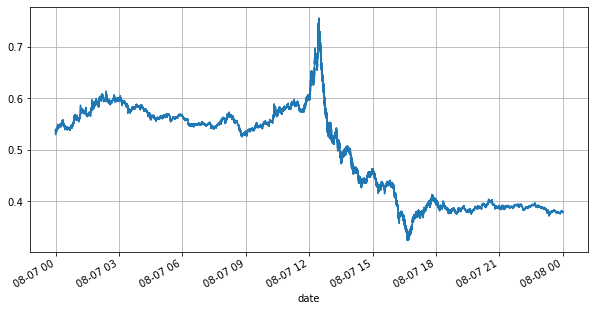
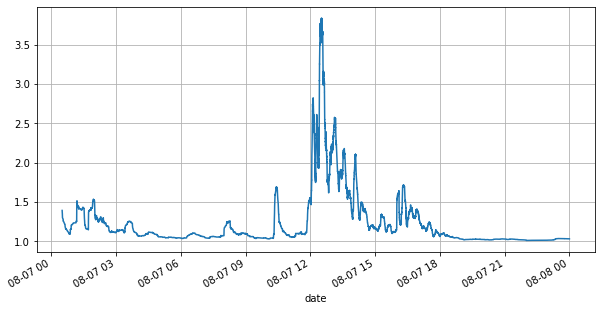
Primeiro, vamos dar uma olhada no mercado do dia. Ele tem grandes altos e baixos. Além disso, o número de ordens pendentes no dia também mudou muito com a flutuação do mercado. Em particular, o spread (a diferença entre o preço de venda e preço de compra) mostrou significativamente a situação de flutuação do mercado. De acordo com as estatísticas do mercado da YGG naquele dia, 20% das vezes o spread foi maior que 1 tick. Nesta era em que vários robôs competem no mercado, essa situação é rara.

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

books = pd.read_csv('YGGUSDT-bookTicker-2023-08-07.csv')

tick_size = 0.0001

books['date'] = pd.to_datetime(books['transaction_time'], unit='ms')
books.index = books['date']

books['spread'] = round(books['best_ask_price'] - books['best_bid_price'],4)

books['best_bid_price'][::10].plot(figsize=(10,5),grid=True);

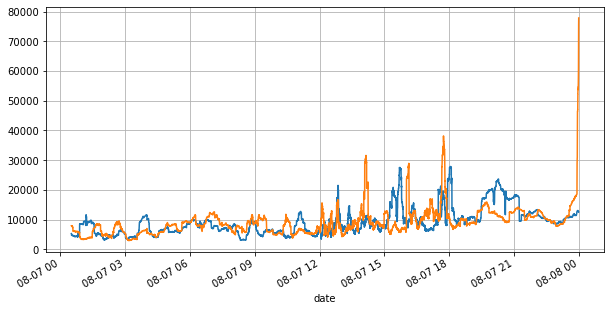
books['best_bid_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);
books['best_ask_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);

(books['spread'][::10]/tick_size).rolling(10000).mean().plot(figsize=(10,5),grid=True);

books['spread'].value_counts()[books['spread'].value_counts()>500]/books['spread'].value_counts().sum()

0.0001    0.799169
0.0002    0.102750
0.0003    0.042472
0.0004    0.022821
0.0005    0.012792
0.0006    0.007350
0.0007    0.004376
0.0008    0.002712
0.0009    0.001657
0.0010    0.001089
0.0011    0.000740
0.0012    0.000496
0.0013    0.000380
0.0014    0.000258
0.0015    0.000197
0.0016    0.000140
0.0017    0.000112
0.0018    0.000088
0.0019    0.000063
Name: spread, dtype: float64

Citações Desequilibradas

Do exposto acima, podemos ver que os volumes de ordens de compra e venda são muito diferentes na maioria das vezes. Essa diferença tem um forte efeito preditivo nas condições de mercado de curto prazo. O motivo é semelhante ao mencionado no artigo anterior: pequenas ordens de compra geralmente levam a quedas. Se as ordens pendentes de um lado forem significativamente menores do que as do outro lado, e assumindo que os volumes de ordens ativas de compra e venda sejam próximos, o lado com as ordens pendentes menores terá maior probabilidade de ser consumido, aumentando assim o preço. mudanças. Aspas desbalanceadas são representadas por I: 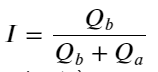Onde Q_b representa a quantidade da ordem de compra (best_bid_qty) e Q_a representa a quantidade da ordem de venda (best_ask_qty).

Defina preço médio: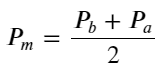

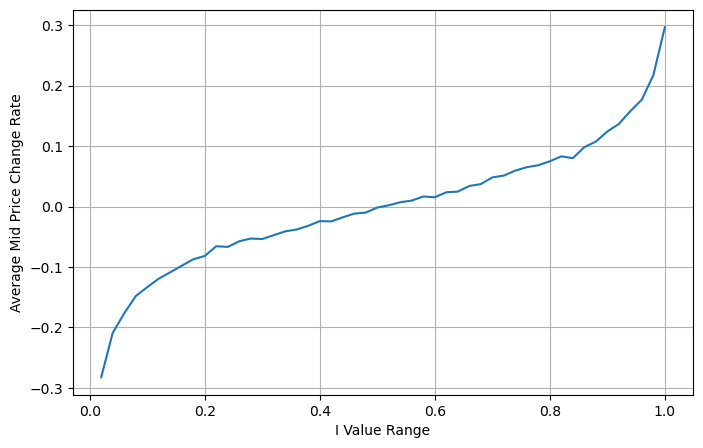
A figura a seguir mostra a relação entre a taxa de variação do preço médio no próximo intervalo e o desequilíbrio I. Como esperado, à medida que I aumenta, o preço tem maior probabilidade de subir e quanto mais próximo estiver de 1, maior será a magnitude do desequilíbrio. a mudança de preço também é acelerada. No trading de alta frequência, o propósito de introduzir o preço médio é prever melhor as mudanças futuras de preço. Em outras palavras, quanto menor a diferença do preço futuro, melhor o preço médio é definido. Obviamente, o desequilíbrio de ordens pendentes fornece informações adicionais para a previsão da estratégia. Levando isso em consideração, definimos o preço médio ponderado:

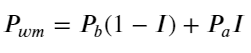
books['I'] = books['best_bid_qty'] / (books['best_bid_qty'] + books['best_ask_qty'])

books['mid_price'] = (books['best_ask_price'] + books['best_bid_price'])/2

bins = np.linspace(0, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['price_change'] = (books['mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Average Mid Price Change Rate');
plt.grid(True)

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['weighted_price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

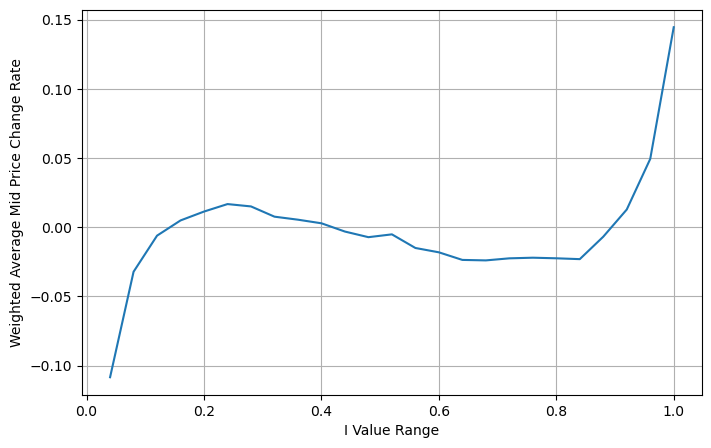
Ajuste do preço médio ponderado

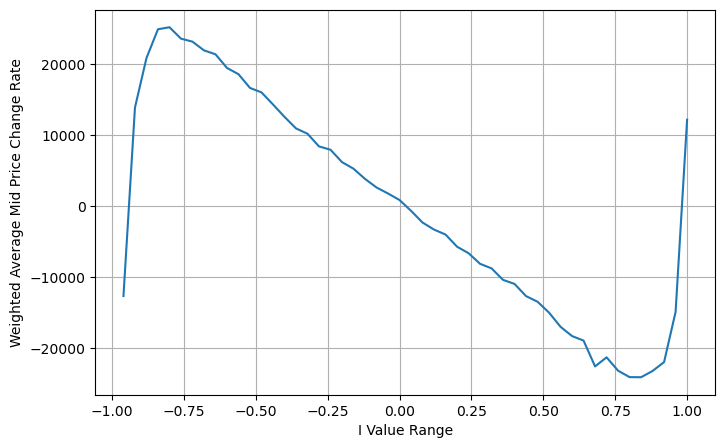
Na figura, podemos ver que o preço médio ponderado muda muito menos que diferentes I, o que significa que o preço médio ponderado é um ajuste melhor. Mas ainda há algumas regularidades, como em torno de 0,2 e 0,8, onde os desvios são relativamente grandes. Isso mostra que ainda posso contribuir com informações adicionais. Como o preço médio ponderado assume que o termo de correção de preço é completamente linear com I, isso obviamente não é verdade. Como pode ser visto na figura acima, quando I está próximo de 0 e 1, o desvio é mais rápido e não é um relação linear.

Para uma visão mais intuitiva, I é redefinido aqui:

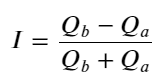
Neste momento:

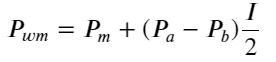
Observando esta forma, podemos descobrir que o preço médio ponderado é uma correção para o preço médio médio. O coeficiente do termo de correção é Spread, e o termo de correção é uma função de I. O preço médio ponderado simplesmente assume que essa relação é I/2. Neste momento, a vantagem da distribuição ajustada de I (-1,1) é refletida. I é simétrica em relação à origem, o que torna conveniente para nós encontrarmos a relação de ajuste da função. Observe o gráfico, esta função deve satisfazer a relação de potência ímpar de I, que é consistente com o rápido crescimento em ambos os lados e simetria sobre a origem. Além disso, pode-se observar que o valor próximo à origem é próximo de linear, e quando I é 0, o resultado da função é 0, e quando I é 1, o resultado da função é 0,5. Então acho que essa função se parece com:

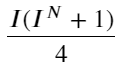
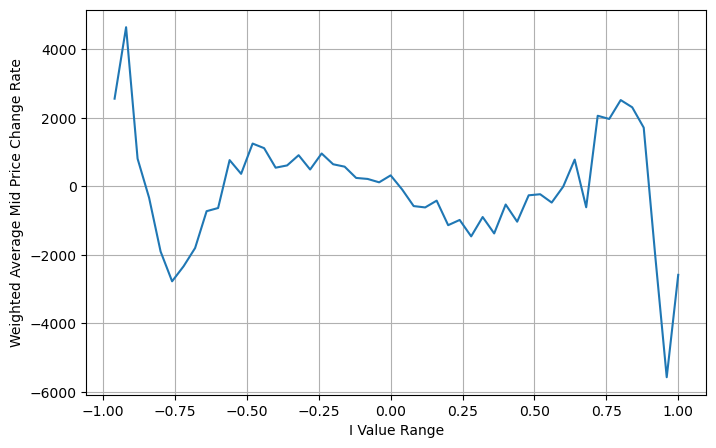
Aqui N é um número par positivo. Após testes reais, é melhor quando N é 8. Até agora, este artigo propõe um preço médio ponderado revisado:

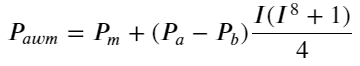
Neste ponto, a mudança no preço médio previsto não tem basicamente nada a ver com I. Embora esse resultado seja melhor do que o preço médio ponderado simples, ele não pode ser aplicado em negociações reais. É apenas uma ideia dada aqui. Um artigo de 2017 de S Stoikov introduziu o método da cadeia de MarkovMicro-Price, e fornece o código relevante, você também pode estudá-lo.

books['I'] = (books['best_bid_qty'] - books['best_ask_qty']) / (books['best_bid_qty'] + books['best_ask_qty'])

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['weighted_price_change'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I'])*(books['I']**8+1)/4
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

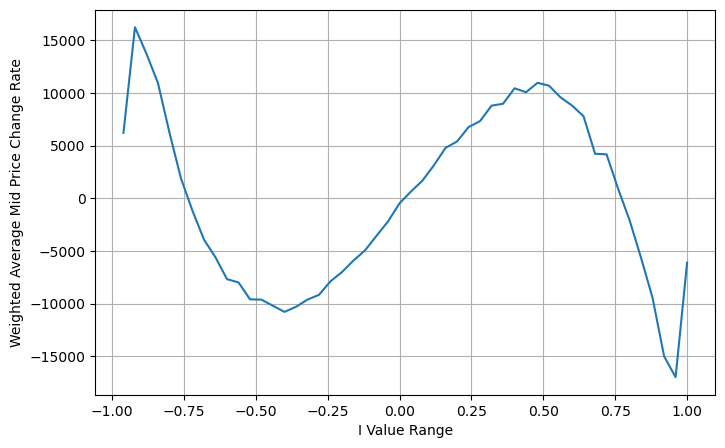
books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I']**3)/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

Resumir

O preço médio é muito importante para estratégias de alta frequência. É uma previsão de preços futuros de curto prazo, então o preço médio deve ser o mais preciso possível. Os preços médios apresentados acima são todos baseados em dados de mercado, porque apenas um preço de mercado é usado na análise. Na negociação real, a estratégia deve usar todos os dados o máximo possível, especialmente quando há trocas comerciais na negociação real, e a previsão do preço médio deve ser testada pelo preço real da transação. Lembro que Stoikov parece ter postado um tweet dizendo que o preço médio real deveria ser a média ponderada da probabilidade de uma transação de compra e venda. Essa questão acabou de ser estudada no artigo anterior. Devido ao espaço limitado, essas questões serão discutidas em detalhes no próximo artigo.