O artigo anterior deu uma introdução preliminar aos métodos de cálculo de vários preços médios e deu uma revisão do preço médio. Este artigo continua a se aprofundar neste tópico.

Dados requeridos

Os dados do fluxo de ordens e dez níveis de dados de profundidade são coletados de negociações reais, e a frequência de atualização é de 100 ms. O mercado real contém apenas os dados de compra e venda, que são atualizados em tempo real. Por uma questão de simplicidade, não é usado por enquanto. Considerando que os dados são muito grandes, apenas 100.000 linhas de dados detalhados são retidas, e as condições de mercado para cada nível também são separadas em colunas separadas.

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import ast
%matplotlib inline

tick_size = 0.0001

trades = pd.read_csv('YGGUSDT_aggTrade.csv',names=['type','event_time', 'agg_trade_id','symbol', 'price', 'quantity', 'first_trade_id', 'last_trade_id',
       'transact_time', 'is_buyer_maker'])

trades = trades.groupby(['transact_time','is_buyer_maker']).agg({
    'transact_time':'last',
    'agg_trade_id': 'last',
    'price': 'first',
    'quantity': 'sum',
    'first_trade_id': 'first',
    'last_trade_id': 'last',
    'is_buyer_maker': 'last',
})

trades.index = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index.rename('time', inplace=True)
trades['interval'] = trades['transact_time'] - trades['transact_time'].shift()

depths = pd.read_csv('YGGUSDT_depth.csv',names=['type','event_time', 'transact_time','symbol', 'u1', 'u2', 'u3', 'bids','asks'])

depths = depths.iloc[:100000]

depths['bids'] = depths['bids'].apply(ast.literal_eval).copy()
depths['asks'] = depths['asks'].apply(ast.literal_eval).copy()

def expand_bid(bid_data):
    expanded = {}
    for j, (price, quantity) in enumerate(bid_data):
        expanded[f'bid_{j}_price'] = float(price)
        expanded[f'bid_{j}_quantity'] = float(quantity)
    return pd.Series(expanded)
def expand_ask(ask_data):
    expanded = {}
    for j, (price, quantity) in enumerate(ask_data):
        expanded[f'ask_{j}_price'] = float(price)
        expanded[f'ask_{j}_quantity'] = float(quantity)
    return pd.Series(expanded)
# 应用到每一行，得到新的df
expanded_df_bid = depths['bids'].apply(expand_bid)
expanded_df_ask = depths['asks'].apply(expand_ask)
# 在原有df上进行扩展
depths = pd.concat([depths, expanded_df_bid, expanded_df_ask], axis=1)

depths.index = pd.to_datetime(depths['transact_time'], unit='ms')
depths.index.rename('time', inplace=True);

trades = trades[trades['transact_time'] < depths['transact_time'].iloc[-1]]

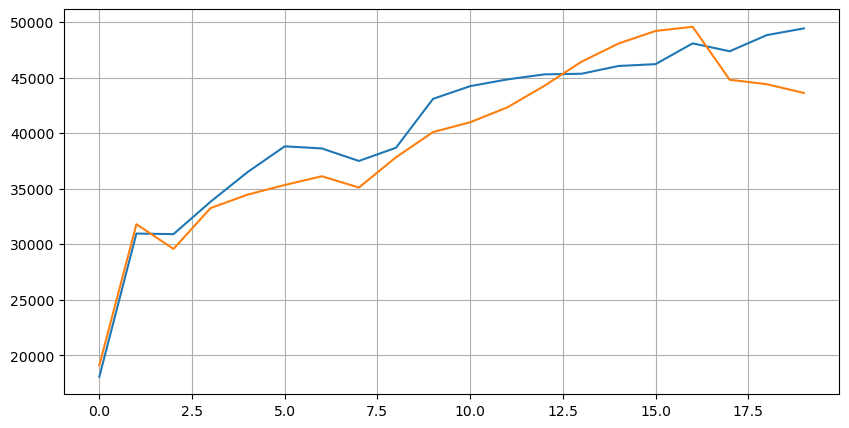
Vamos primeiro olhar para a distribuição dessas 20 condições de mercado. Ela está em linha com as expectativas. Quanto mais distante da abertura do mercado, mais ordens pendentes há, e as ordens de compra e venda são aproximadamente simétricas.

bid_mean_list = []
ask_mean_list = []
for i in range(20):
    bid_mean_list.append(round(depths[f'bid_{i}_quantity'].mean(),0))
    ask_mean_list.append(round(depths[f'ask_{i}_quantity'].mean(),0))
plt.figure(figsize=(10, 5))
plt.plot(bid_mean_list);
plt.plot(ask_mean_list);
plt.grid(True)

Combine dados de profundidade e dados de transações para facilitar a avaliação da precisão da previsão. Aqui garantimos que os dados da transação sejam todos posteriores aos dados de profundidade. Sem considerar o atraso, calculamos diretamente o erro quadrático médio entre o valor previsto e o preço real da transação. Usado para medir a precisão das previsões.

A julgar pelos resultados, o erro de mid_price, a média do par buy-sell, é o maior. Após mudar para weight_mid_price, o erro imediatamente se torna muito menor, e é melhorado ainda mais ajustando o preço médio ponderado. Depois que o artigo de ontem foi publicado, algumas pessoas relataram que usaram apenas I^³⁄₂. Verifiquei aqui e descobri que o resultado foi melhor. Depois de pensar sobre o motivo, deve ser a diferença na frequência de eventos. Quando I está próximo de -1 e 1, é um evento de baixa probabilidade. Para corrigir essas baixas probabilidades, a previsão de eventos de alta frequência não é tão preciso. Portanto, em mais Para cuidar de eventos de alta frequência, fiz alguns ajustes (esses são parâmetros puramente experimentais e não são muito úteis para negociação real):

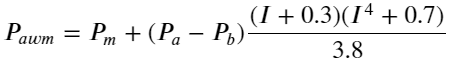
O resultado foi um pouco melhor. Conforme mencionado no artigo anterior, as estratégias devem ser previstas com mais dados. Com mais profundidade e dados de atendimento de pedidos, a melhoria que pode ser obtida pelo emaranhamento com o preço de mercado já é muito fraca.

df = pd.merge_asof(trades, depths, on='transact_time', direction='backward')

df['spread'] = round(df['ask_0_price'] - df['bid_0_price'],4)
df['mid_price'] = (df['bid_0_price']+ df['ask_0_price']) / 2
df['I'] = (df['bid_0_quantity'] - df['ask_0_quantity']) / (df['bid_0_quantity'] + df['ask_0_quantity'])
df['weight_mid_price'] = df['mid_price'] + df['spread']*df['I']/2
df['adjust_mid_price'] = df['mid_price'] + df['spread']*(df['I'])*(df['I']**8+1)/4
df['adjust_mid_price_2'] = df['mid_price'] + df['spread']*df['I']*(df['I']**2+1)/4
df['adjust_mid_price_3'] = df['mid_price'] + df['spread']*df['I']**3/2
df['adjust_mid_price_4'] = df['mid_price'] + df['spread']*(df['I']+0.3)*(df['I']**4+0.7)/3.8

print('平均值     mid_price的误差：', ((df['price']-df['mid_price'])**2).sum())
print('挂单量加权 mid_price的误差：', ((df['price']-df['weight_mid_price'])**2).sum())
print('调整后的   mid_price的误差：', ((df['price']-df['adjust_mid_price'])**2).sum())
print('调整后的 mid_price_2的误差：', ((df['price']-df['adjust_mid_price_2'])**2).sum())
print('调整后的 mid_price_3的误差：', ((df['price']-df['adjust_mid_price_3'])**2).sum())
print('调整后的 mid_price_4的误差：', ((df['price']-df['adjust_mid_price_4'])**2).sum())

平均值     mid_price的误差： 0.0048751924999999845
挂单量加权 mid_price的误差： 0.0048373440193987035
调整后的   mid_price的误差： 0.004803654771638586
调整后的 mid_price_2的误差： 0.004808216498329721
调整后的 mid_price_3的误差： 0.004794984755260528
调整后的 mid_price_4的误差： 0.0047909595497071375

Considere a profundidade da segunda marcha

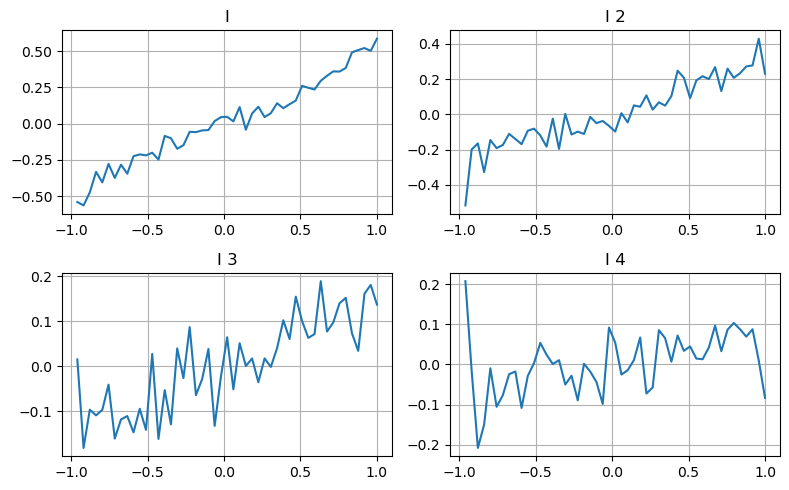
Aqui usamos a ideia do artigo anterior para examinar as diferentes faixas de valor de um determinado parâmetro de influência e as mudanças no preço da transação para medir a contribuição desse parâmetro para o preço médio. Conforme mostrado no gráfico de profundidade de primeiro nível, à medida que I aumenta, o próximo preço de transação tem maior probabilidade de mudar positivamente, o que significa que I faz uma contribuição positiva.

O segundo lote foi processado da mesma maneira e verificou-se que, embora o efeito tenha sido ligeiramente menor que o do primeiro lote, ele ainda não foi desprezível. O terceiro nível de profundidade também faz uma pequena contribuição, mas a monotonicidade é muito pior, e profundidades maiores basicamente não têm valor de referência.

De acordo com os diferentes níveis de contribuição, diferentes pesos são atribuídos aos parâmetros de desequilíbrio dos três níveis. A inspeção real mostra que os erros de previsão são ainda mais reduzidos para diferentes métodos de cálculo.

bins = np.linspace(-1, 1, 50)
df['change'] = (df['price'].pct_change().shift(-1))/tick_size
df['I_bins'] = pd.cut(df['I'], bins, labels=bins[1:])
df['I_2'] = (df['bid_1_quantity'] - df['ask_1_quantity']) / (df['bid_1_quantity'] + df['ask_1_quantity'])
df['I_2_bins'] = pd.cut(df['I_2'], bins, labels=bins[1:])
df['I_3'] = (df['bid_2_quantity'] - df['ask_2_quantity']) / (df['bid_2_quantity'] + df['ask_2_quantity'])
df['I_3_bins'] = pd.cut(df['I_3'], bins, labels=bins[1:])
df['I_4'] = (df['bid_3_quantity'] - df['ask_3_quantity']) / (df['bid_3_quantity'] + df['ask_3_quantity'])
df['I_4_bins'] = pd.cut(df['I_4'], bins, labels=bins[1:])
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(8, 5))


axes[0][0].plot(df.groupby('I_bins')['change'].mean())
axes[0][0].set_title('I')
axes[0][0].grid(True)

axes[0][1].plot(df.groupby('I_2_bins')['change'].mean())
axes[0][1].set_title('I 2')
axes[0][1].grid(True)

axes[1][0].plot(df.groupby('I_3_bins')['change'].mean())
axes[1][0].set_title('I 3')
axes[1][0].grid(True)

axes[1][1].plot(df.groupby('I_4_bins')['change'].mean())
axes[1][1].set_title('I 4')
axes[1][1].grid(True)
plt.tight_layout();

df['adjust_mid_price_4'] = df['mid_price'] + df['spread']*(df['I']+0.3)*(df['I']**4+0.7)/3.8
df['adjust_mid_price_5'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2'])/2
df['adjust_mid_price_6'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2'])**3/2
df['adjust_mid_price_7'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2']+0.3)*((0.7*df['I']+0.3*df['I_2'])**4+0.7)/3.8
df['adjust_mid_price_8'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.2*df['I_2']+0.1*df['I_3']+0.3)*((0.7*df['I']+0.3*df['I_2']+0.1*df['I_3'])**4+0.7)/3.8

print('调整后的 mid_price_4的误差：', ((df['price']-df['adjust_mid_price_4'])**2).sum())
print('调整后的 mid_price_5的误差：', ((df['price']-df['adjust_mid_price_5'])**2).sum())
print('调整后的 mid_price_6的误差：', ((df['price']-df['adjust_mid_price_6'])**2).sum())
print('调整后的 mid_price_7的误差：', ((df['price']-df['adjust_mid_price_7'])**2).sum())
print('调整后的 mid_price_8的误差：', ((df['price']-df['adjust_mid_price_8'])**2).sum())

调整后的 mid_price_4的误差： 0.0047909595497071375
调整后的 mid_price_5的误差： 0.0047884350488318714
调整后的 mid_price_6的误差： 0.0047778319053133735
调整后的 mid_price_7的误差： 0.004773578540592192
调整后的 mid_price_8的误差： 0.004771415189297518

Considere os dados da transação

Os dados da transação refletem diretamente o grau de posições longas e curtas. Afinal, esta é uma opção que envolve dinheiro real, e o custo de colocar uma ordem é muito menor, e há até casos de fraude deliberada de colocação de ordem. Portanto, ao prever o preço médio, a estratégia deve se concentrar nos dados de transação.

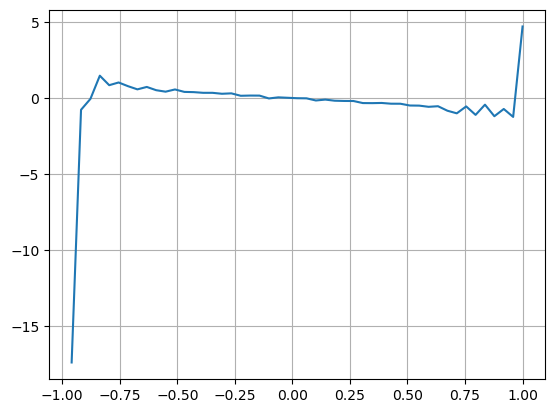
Considerando a forma, defina o desequilíbrio da quantidade média de chegada do pedido VI, Vb, Vs representam a quantidade média de ordens de compra e ordens de venda por evento unitário, respectivamente.

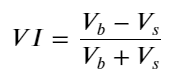
Os resultados mostram que a quantidade de chegada em um curto período de tempo é a mais significativa na previsão de mudanças de preço. Quando o VI está entre (0,1-0,9), ele é negativamente correlacionado com o preço, mas fora do intervalo ele é positivamente correlacionado com o preço. Isso sugere que quando o mercado não é extremo, ele é caracterizado principalmente por flutuações e os preços retornarão à média. Quando ocorrem condições extremas de mercado, como um grande número de ordens de compra sobrepujando ordens de venda, a tendência sairá da tendência . Mesmo se ignorarmos essas situações de baixa probabilidade e simplesmente assumirmos que a tendência e o VI satisfazem uma relação linear negativa, o erro de previsão do preço médio é bastante reduzido. O a na fórmula representa o coeficiente.

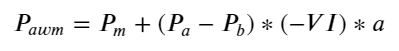
alpha=0.1

df['avg_buy_interval'] = None
df['avg_sell_interval'] = None
df.loc[df['is_buyer_maker'] == True, 'avg_buy_interval'] = df[df['is_buyer_maker'] == True]['transact_time'].diff().ewm(alpha=alpha).mean()
df.loc[df['is_buyer_maker'] == False, 'avg_sell_interval'] = df[df['is_buyer_maker'] == False]['transact_time'].diff().ewm(alpha=alpha).mean()

df['avg_buy_quantity'] = None
df['avg_sell_quantity'] = None
df.loc[df['is_buyer_maker'] == True, 'avg_buy_quantity'] = df[df['is_buyer_maker'] == True]['quantity'].ewm(alpha=alpha).mean()
df.loc[df['is_buyer_maker'] == False, 'avg_sell_quantity'] = df[df['is_buyer_maker'] == False]['quantity'].ewm(alpha=alpha).mean()

df['avg_buy_quantity'] = df['avg_buy_quantity'].fillna(method='ffill')
df['avg_sell_quantity'] = df['avg_sell_quantity'].fillna(method='ffill')
df['avg_buy_interval'] = df['avg_buy_interval'].fillna(method='ffill')
df['avg_sell_interval'] = df['avg_sell_interval'].fillna(method='ffill')

df['avg_buy_rate'] = 1000 / df['avg_buy_interval']
df['avg_sell_rate'] =1000 / df['avg_sell_interval']

df['avg_buy_volume'] = df['avg_buy_rate']*df['avg_buy_quantity']
df['avg_sell_volume'] = df['avg_sell_rate']*df['avg_sell_quantity']

df['I'] = (df['bid_0_quantity']- df['ask_0_quantity']) / (df['bid_0_quantity'] + df['ask_0_quantity'])
df['OI'] = (df['avg_buy_rate']-df['avg_sell_rate']) / (df['avg_buy_rate'] + df['avg_sell_rate'])
df['QI'] = (df['avg_buy_quantity']-df['avg_sell_quantity']) / (df['avg_buy_quantity'] + df['avg_sell_quantity'])
df['VI'] = (df['avg_buy_volume']-df['avg_sell_volume']) / (df['avg_buy_volume'] + df['avg_sell_volume'])

bins = np.linspace(-1, 1, 50)
df['VI_bins'] = pd.cut(df['VI'], bins, labels=bins[1:])
plt.plot(df.groupby('VI_bins')['change'].mean());
plt.grid(True)

df['adjust_mid_price'] = df['mid_price'] + df['spread']*df['I']/2
df['adjust_mid_price_9'] = df['mid_price'] + df['spread']*(-df['OI'])*2
df['adjust_mid_price_10'] = df['mid_price'] + df['spread']*(-df['VI'])*1.4

print('调整后的mid_price   的误差：', ((df['price']-df['adjust_mid_price'])**2).sum())
print('调整后的mid_price_9 的误差：', ((df['price']-df['adjust_mid_price_9'])**2).sum())
print('调整后的mid_price_10的误差：', ((df['price']-df['adjust_mid_price_10'])**2).sum())

调整后的mid_price   的误差： 0.0048373440193987035
调整后的mid_price_9 的误差： 0.004629586542840461
调整后的mid_price_10的误差： 0.004401790287167206

Preço médio abrangente

Considerando que tanto os pedidos pendentes quanto os dados de transação são úteis para prever o preço médio, esses dois parâmetros podem ser combinados. A atribuição de peso aqui é arbitrária e não considera as condições de contorno. Em casos extremos, o preço médio previsto pode ser Não é entre comprar um e vender um, mas desde que o erro possa ser reduzido, esses detalhes não importam.

Finalmente, o erro de previsão caiu do inicial 0,00487 para 0,0043. Não entraremos em detalhes aqui. Ainda há muito a explorar sobre o preço médio. Afinal, prever o preço médio é prever o preço. Você pode tentar você mesmo .

#注意VI需要延后一个使用
df['price_change'] = np.log(df['price']/df['price'].rolling(40).mean())
df['CI'] = -1.5*df['VI'].shift()+0.7*(0.7*df['I']+0.2*df['I_2']+0.1*df['I_3'])**3 + 150*df['price_change'].shift(1)

df['adjust_mid_price_11'] = df['mid_price'] + df['spread']*(df['CI'])
print('调整后的mid_price_11的误差：', ((df['price']-df['adjust_mid_price_11'])**2).sum())

调整后的mid_price_11的误差： 0.00421125960463469

Resumir

Este artigo combina dados de profundidade e dados de transação para melhorar ainda mais o método de cálculo do preço médio. Este artigo fornece um método para medir a precisão e melhora a precisão da previsão de mudanças de preço. No geral, os vários parâmetros não são muito rigorosos e servem apenas para referência. Com um preço médio mais preciso, o próximo passo é realmente aplicar o preço médio para backtesting. Esta parte também tem muito conteúdo, então vamos parar de atualizar por um tempo.