В этой статье мы рассмотрим процесс Орнштейна-Уленбека, опишем его математические формулы, реализуем и моделируем его с помощью Python, и обсудим некоторые практические приложения в количественных финансовых и системных сделках. Мы будем использовать более продвинутую модель случайных процессов, называемую процессом Орнштейна-Уленбека (OU), которая может быть использована для моделирования временных последовательностей, демонстрирующих равнозначное поведение. Это особенно полезно для моделирования процентной ставки в определении цен на производные товары, а также для алгоритмизации системных сделок при торговле.

Что такое процесс Орнштейна-Уленбека?

Процесс Орнштейна-Уленбека (англ. Ornstein-Uhlenbeck process) - это непрерывный временной случайный процесс, используемый для моделирования равнозначного регрессивного поведения. Это означает, что в отличие от стандартных случайных поворотов или движений Брауна, которые могут дрейфовать бесконечно, процесс ОУ часто возвращается к долгосрочным средним значениям с течением времени.

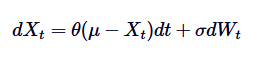
В них Xt представляет собой случайный процесс во времени t, μ - долгосрочная средняя величина, θ - средняя скорость возврата, δ - волатильность, а dWt - процесс Винера или стандартное движение Брауна.

Историческое происхождение и применение

Процесс Орнштейна-Уленбека был первоначально предложен Леонардом Орнштейном и Джорджем Юджином Уленбеком в 1930 году для моделирования скорости частиц, которые совершают движение по Брауну при наличии трения. Со временем его практическая польза вышла далеко за пределы физики, и его применяют в различных областях, таких как биология, химия, экономика и финансы.

В квантовой финансовой системе процесс ОУ особенно полезен для моделирования явлений, демонстрирующих регрессию средней стоимости. Примером является волатильность процентных ставок, обменных курсов и финансовых рынков. Например, популярная модель процентных ставок - модель Васичека - выведена непосредственно из процесса ОУ.

Значение в квантовом финансировании

Процесс Орнштейна-Уленбека имеет важное значение в квантовой финансовой системе по следующим причинам: его регрессивный характер средней величины делает его естественным выбором для моделирования финансовых переменных, которые не демонстрируют случайных поворотов, а колеблются вокруг стабильных долгосрочных средних величин. Эта особенность важна для моделирования процентных ставок, где регрессивная средняя величина отражает влияние центральных банков на долгосрочные стабильные процентные ставки.

Кроме того, OU-процесс также используется в моделях ценообразования активов (включая оценку производных) и в стратегиях управления рисками. Он также может служить строительными блоками более сложных моделей, таких как модель Cox-Ingersoll-Ross (CIR), которая расширяет OU-процесс для моделирования процентной ставки с неотрицательной стоимостью.

Основные особенности и интуиция

Основные особенности процесса Орнштейна-Уленбека можно обобщить следующим образом:

• Возвращение среднего значения:Процессы OU имеют тенденцию к возврату к долгосрочным средним значениям μ. Это в отличие от таких процессов, как движения Брауна, которые не демонстрируют такой тенденции.
• Волатильность:Уровень случайности или волатильности в процессе управления параметром δ. Чем выше волатильность, тем больше отклонение процесса от среднего значения до возвращения.
• Скорость возвращения:Параметр θ определяет скорость возвращения процесса к среднему значению. Чем выше значение θ, тем быстрее возвращается среднее значение.
• Устойчивость:Процесс OU является устойчивым, что означает, что его статистические характеристики не изменяются со временем. Это важно для моделирования стабильной системы в финансовом секторе.

Интуитивно говоря, вы можете рассматривать процесс Орнштейна-Уленбека как моделирование поведения костной ткани, которая растягивается вокруг среднего значения. Хотя процесс может отклоняться от среднего значения из-за случайных колебаний, растягивающийся кузов костной ткани (аналогично возвращению к среднему значению) гарантирует, что он в конечном итоге вернется к среднему значению.

Сравнение с другими случайными процессами

Процесс ОУ, так как он тесно связан с моделированием различных финансовых явлений, его часто сравнивают с другими случайными процессами, такими как движения Брауна и геометрические движения Брауна (GBM). В отличие от движения Брауна, в котором нет тенденции к возврату средних значений, процесс ОУ обладает явным возвратом средних значений. Это делает его более подходящим для моделирования сценариев, в которых переменные колеблются вокруг стабильного равновесного колебания.

По сравнению с GBM, который обычно используется для моделирования цен на акции и включает в себя элементы дрейфа и колебаний, процесс OU не показывает индексный рост, а колеблется вокруг его средней стоимости. GBM более подходит для моделирования количества, которое растет с течением времени, а процесс OU очень подходит для моделирования переменных, которые показывают характеристики средней стоимости.

Примеры квантового финансирования

Процесс Орнштейна-Уленбека имеет широкое применение в финансовой сфере, особенно в модельных сценариях с среднезначным возвратом как ключевой характеристикой. Ниже мы обсудим некоторые из наиболее распространенных случаев использования.

Моделирование процентных ставок

Одним из наиболее заметных применений процесса ОУ является моделирование процентных ставок, особенно в рамках модели Васичека. Модель Васичека предполагает, что процентные ставки следуют процессу ОУ, то есть ставки часто возвращаются к долгосрочным средним значениям с течением времени. Эта особенность важна для точного моделирования поведения процентных ставок, поскольку ставки часто колеблются не бесконечно, а около средних уровней, подверженных влиянию экономических условий.

Ценообразование активов

В ценах на активы, особенно на фиксированные доходы, ОУ-процесс обычно используется для моделирования эволюции доходности облигаций. Регрессивная природа средней стоимости ОУ-процесса гарантирует, что доходность не отклоняется слишком далеко от ее исторической средней стоимости, что согласуется с наблюдаемой рыночной деятельностью. Это делает ОУ-процесс ценным инструментом для ценообразования облигаций и других чувствительных к процентной ставке инструментов.

Пара торговой стратегии

Паровая торговля - это рыночно-нейтральная стратегия, которая включает в себя создание компенсирующих позиций в двух связанных активах. В этом случае процесс OU особенно полезен, поскольку он позволяет моделировать разницу в цене между двумя активами, а разница обычно является средневзвешенной. Используя процесс OU для моделирования разрыва в цене, трейдер может подтвердить прибыльные входные и выходные точки, прогнозировать средневзвешенную возвратность и, таким образом, генерировать торговый сигнал.

Например, если разрыв между двумя фьючерсами расширяется до превышения определенного отклонения, трейдеры могут списать с учета наиболее эффективные фьючерсы и продать наиболее неэффективные, надеясь, что разрыв вернется к своему историческому среднему уровню, что позволит получить прибыль при повороте.

Решение Ornstein-Uhlenbeck SDE

Формула дифференциального уравнения процесса Орнштейна-Уленбека является основой его решения. Для решения данного SDE мы использовали метод интегральных факторов. Давайте перепишем SDE:

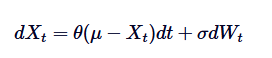
Сначала мы умножим обе стороны на интегральный фактор /upload/asset/28dfe9abfb54772651590.png:

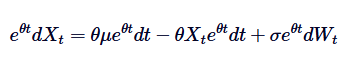
Обратите внимание, что если мы добавим 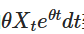на обе стороны, то левая сторона может быть представлена как разница в произведении:

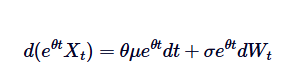
Если мы интегрируем обе стороны от 0 до t, мы получим:

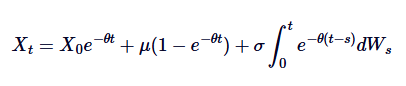
Это общее определение Орнштейна-Уленбека SDE.

Выводы, приведенные выше, имеют несколько важных значений. Первый пункт 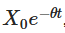указывает на то, что первоначальные значения со временем уменьшаются, и показывает, как процесс постепенно забывает о своей начальной точке. Второй пункт 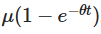указывает на то, что процесс со временем приближается к среднему значению μ. Третий пункт вводит случайность, в которой интегралы процесса, связанные с процессом Wiener, объясняют случайные колебания.

Это решение подчеркивает баланс между регрессионным поведением среднего значения определенности и случайным количеством, управляемым движением Брауна. Понимание этого решения имеет важное значение для эффективного моделирования процесса ОУ, как описано ниже.

Связь с другими случайными процессами

Процесс Орнштейна-Уленбека имеет несколько важных связей с другими известными случайными процессами (включая движение Брауна и модель Васичека).

Связь с движением Браун

Процесс Орнштейна-Уленбека можно рассматривать как средневзвешенную версию движения Брауна. Движение Брауна описывает процесс, имеющий тенденцию к независимому приросту и не имеющий средневзвешенного возврата, а процесс ОУ вводит средневзвешенное возврата, изменяя движение Брауна с помощью дрейфующего элемента, что приводит к возврату процесса к центральному значению.

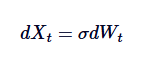
Таким образом, движение Брауна является особым примером процесса OU, соответствующим отсутствию среднезначного возвращения.

Связь с моделью Васикека

Модель Васичека широко используется для моделирования процентной ставки, и по сути является приложением процесса Орнштейна-Уленбека в эволюции процентной ставки. Модель Васичека предполагает, что процентная ставка следует процессу ОУ, где SDE определяется как:

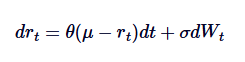
Из них rt обозначает краткосрочную процентную ставку, а интерпретация параметров θ, μ и δ аналогична интерпретации в процессе ОУ. Модель Васичека способна генерировать средневзвешенный возвратный путь процентных ставок, что является одним из ее основных преимуществ в финансовом моделировании.

Понимание этих связей позволяет получить более широкое представление о том, как процесс ОУ используется в различных средах, особенно в финансовой сфере. Мы рассмотрим практические значения этих связей, обсуждая примеры применения ниже.

Моделирование процесса Орнштейна-Уленбека с помощью Python

В этом разделе мы рассмотрим, как использовать Python для моделирования процесса Ornstein-Uhlenbeck (OU). Это связано с использованием дифференциации Euler-Maruyama для дифференциации случайных микродифференциальных уравнений, определяющих процесс OU (SDE).

Разделение SDE

Давайте вернемся к математическим формулам SDE, описанным выше, и рассмотрим каждый термин:

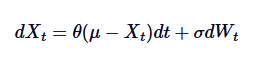
в,

• Xt - значение процесса во времени t.
• θ - скорость среднезначной регрессии.
• μ - долгосрочная средняя величина процесса.
• δ - параметр колебания.
• dWt обозначает прирост процесса Винера (стандартное движение Брауна).

Для того, чтобы смоделировать этот процесс на компьютере, нам необходимо провести дифференциацию SDE на непрерывное время. Одним из наиболее распространенных методов является дифференциация Эйлера-Маруямы, которая приближает непрерывный процесс, учитывая небольшие шаги времени дифференциации /upload/asset/28db85708af6d062dda8d.png. Дифференциальная форма процесса Орнштейна-Ухленбека дается следующей формулой:

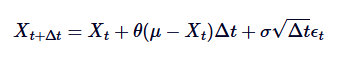
В частности, 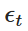является случайной переменной, извлеченной из стандартного нормального распределения (т.е. 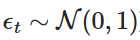). Такая дифференциация позволяет нам вычислить значение Xt по времени, чтобы имитировать поведение процесса OU.

Реализация Python

Теперь давайте реализуем дифференцированный процесс Ornstein-Uhlenbeck в Python. В данном контексте мы будем использовать только библиотеки Python NumPy и Matplotlib.

Сначала мы ввозим NumPy и Matplotlib в стандартном виде. Затем мы задаем все параметры для модели OU. Затем мы заранее распределяем NumPy-арестр длиной N, чтобы после вычисления пути OU добавить его к нему. Затем мы итерации N-1 (шаг 1 - это указано начальное условие X0), моделируем случайный прирост dW, затем вычисляем следующую итерацию пути OU в соответствии с вышеуказанной математической формулой.

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 10.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

Результаты на карте:

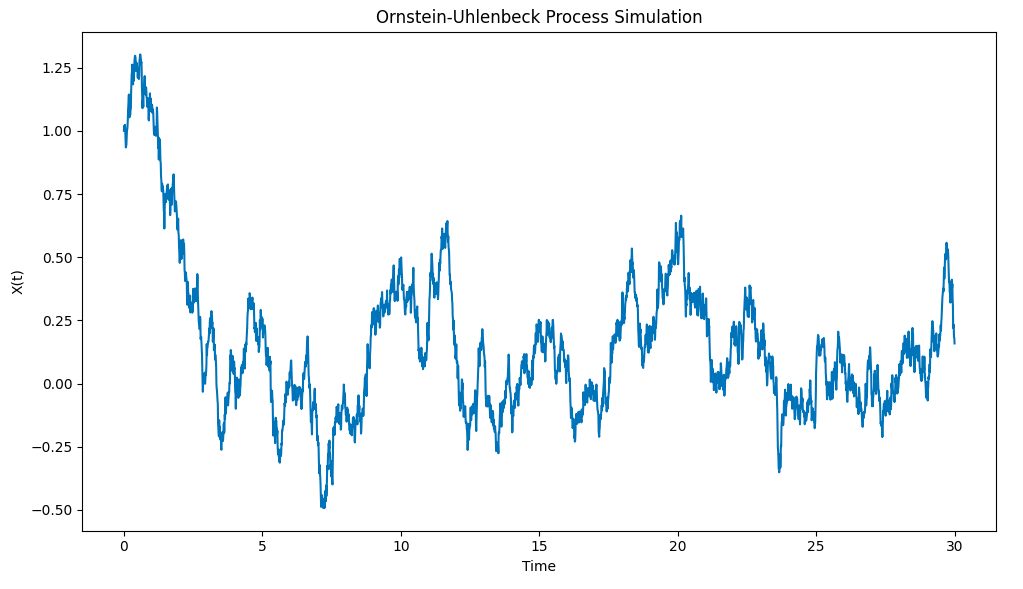
Моделирование процесса Орнштейна-Уленбека с использованием Python

Обратите внимание на то, как этот процесс быстро отталкивается от исходных условий и выводит X0 = 1 до среднего значения μ = 0, а затем, когда он отклоняется от этого среднего значения, он показывает тенденцию к возврату к этому среднему значению.

Резюме и последующие шаги

В этой статье мы обобщили процесс Орнштейна-Уленбека, описали его математические формулы и предоставили базовую реализацию Python для моделирования дискретных версий SDE с непрерывным временем. В последующих статьях мы рассмотрим более сложные SDE, построенные на основе процесса OU, и узнаем, как они используются в системных торговых и производных приложениях ценообразования.

Полный код

# OU process simulation

import numpy as np
import matplotlib.pyplot as plt

# Parameters for the OU process
theta = 0.7      # Speed of mean reversion
mu = 0.0         # Long-term mean
sigma = 0.3      # Volatility
X0 = 1.0         # Initial value
T = 30.0         # Total time
dt = 0.01        # Time step
N = int(T / dt)  # Number of time steps

# Pre-allocate array for efficiency
X = np.zeros(N)
X[0] = X0

# Generate the OU process
for t in range(1, N):
    dW = np.sqrt(dt) * np.random.normal(0, 1)
    X[t] = X[t-1] + theta * (mu - X[t-1]) * dt + sigma * dW

# Plot the result
plt.plot(np.linspace(0, T, N), X)
plt.title("Ornstein-Uhlenbeck Process Simulation")
plt.xlabel("Time")
plt.ylabel("X(t)")
plt.show()

Ссылка на оригинальный текст: https://www.quantstart.com/articles/ornstein-uhlenbeck-simulation-with-python/