Погоня за девушками и поиск ракет - Статистика по формуле Байеса

• ### ONE

Неразборчивый моралист в своей эмоциональной жизни неизбежно столкнется с таким плачем: случайно встретив красивую девушку, которая соответствует его сердцу, он начал долгое путешествие по тайной любви, думая о ней день и ночь, забывая о еде и сне, и ждал, пока однажды, в бесконечных увязках, наконец, набрался смелости признаться девушке, и в итоге девушка сказала:

Для того, чтобы избежать такого рода неудобств, обязательным предметом является точная оценка того, является ли девушка неженатой.

Если вы работаете с девушкой и часто находитесь рядом с ней, то нетрудно понять, является ли она одинокой или нет. Но высокая сложность задачи, которую должны выполнить эти люди, заключается в следующем: как незнакомец, который держит дистанцию с девушкой, можно определить ее одиночество с помощью ограниченной информации, без того, чтобы девушка это заметила.

Первый шаг, чтобы поверить в интуицию. Разумные люди могут подумать о том, чтобы найти нескольких друзей, чтобы тайно наблюдать за девушкой-мишенью, и, конечно, люди, которые ищут, не должны быть умными людьми. Какая группа по идентификации психических расстройств, компрессор слухов, естественный контроль, криминалистический врач, лучше всего найти несколько, женатые люди, сцены, и воры цветов, чем больше людей, тем лучше, чем больше людей, тем лучше.

Для этого мы сделаем второй шаг, будем говорить о фактах и доказательствах. Ответ на вопрос, является ли мужчина или женщина одиноким, можно найти во многих деталях.

Как и в случае с научными исследованиями, можно сначала просмотреть информацию, и в Google можно найти простые и простые критерии, которые многие одинокие люди изучали в течение многих лет, например, принцип мобильного телефона: “влюбленные девушки используют мобильные телефоны чаще”, принцип самообучения: “одинокие девушки часто занимаются сексом с несколькими девушками”).

Подобные статистические данные.

Когда мы получим все эти экспериментальные данные, мы сможем продолжить, скорректировать и оптимизировать вероятность 65,65% из тех, кто только что проголосовал. На что это зависит? Натурально, что целевая девушка выполняет различные критерии. Например, мы обнаружили, что целевая девушка любит заниматься сексом с друзьями, а согласно результатам исследования собственной статистики, мы обнаружили, что среди уже влюбленных девушек, девушки, которые любят заниматься сексом с друзьями, составляют около 60%; среди девушек, которые не влюблены, девушки, которые любят заниматься сексом с друзьями, составляют около 30%;

Так что теперь вероятность того, что мишень mm будет одинокой, превращается в

Я думаю, что в этом случае мы должны быть счастливы и надеяться на большее!

Если в результате исследования также было обнаружено, что у одиноких девушек использование мобильного телефона превышает 1,2 раза в час, что составляет 20%; у девушек, которые уже влюблены, эта цифра составляет 60%.

На этот раз вероятность одиночества вновь упала на 56,02%, и теперь умершие рационалисты могут искать больше критериев оценки, делать больше исследований, постоянно обновлять значение вероятности одиночества девушек, чтобы оно становилось все ближе и ближе к истине, но прежде чем получить окончательный результат, нужно сначала установить порог: вероятность одиночества девушек превышает этот порог (например, 90%), чтобы выяснить, стоит ли это, или же просто умереть.

Однако следует иметь в виду, что независимо от того, сколько раз вычислять, в конечном итоге получается значение вероятности, а не факт, даже если после нескольких исследований можно определить вероятность того, что девушка-цель является одинокой на 99,9%, и сразу же готова признаться ей, но в последнем исследовании наблюдения за девушкой, обнаруженном в семье и мужчиной, держащимся за руки и смеясь, обнимаясь вместе, тогда вероятность одиночества девушки сразу же падает с 99,9% до близкого к нулю.

В данной статье рассказывается о том, что этот научный и строгий логический метод определения того, является ли мм одиноким, называется статистическим методом Бейеса. Метод Бейеса, проще говоря, заключается в том, что предварительная вероятность плюс новые полученные доказательства = вероятность после корректировки.

Впрочем, не стоит пренебрегать изобретением Bayes’s Law, который был придуман сторонниками теории рационализма, так же, как это делают военно-морские силы США в поисках потерянных гидроатомных бомб и пропавших атомных подводных лодок в Тихом океане.

• ### TWO

В один из дней января 1966 года американский бомбардировщик B-52 пролетел над Паломаресом, Испания, и несколько пилотов на борту выполняли задание по воздушному дозаправке, назначенное им командованием ВВС. В принципе, этот полет не был опасен, и пилот, как говорят, был спокойным человеком, который никогда не любил брать большой трубку с двумя отверстиями, даже в кабине самолета.

Но история не закончилась, и после этого произошла череда трагедий и комедий.

В поисках пропавшей гидроатомной бомбы, США спешно направили на место оперативную группу из числа экспертов из США, включая математика по имени Джон Крейвен, который получил звание главного ученого в отделе специальных программ ВМС США.

В поисках гидравлической бомбы, предлагаемой Крейвеном, он использовал только что упомянутый метод Бейеса, он созвал экспертов из разных областей, но каждый из них имеет свою область знаний, и не все знают. Некоторые знают много о бомбардировщиках B-52, но мало знают о свойствах гидравлической бомбы.

Для этих разнообразных вопросов Кравен попросил экспертов сделать различные гипотезы, представить себе различные сценарии, а затем в различных ситуациях предположить вероятность того, что гидравлические бомбы будут находиться в разных местах, а также вероятность возникновения каждой ситуации.

Метод Крейвена также подвергся сомнению со стороны его коллег, поскольку в его программе многие результаты были получены экспертами в виде догадок, голосования и даже азартных игр, и нельзя гарантировать точность всех результатов, но из-за неотложной задачи поиска взрывчатки и отсутствия времени для проведения точных экспериментов и создания полной надежной теории, метод Крейвена не потеряет своего жизнеспособности.

Получив от специалистов данные о том, как была проведена закупка, Крейвен сопоставил их и составил карту вероятности расположения бомбы: разделив всю возможную область на множество маленьких квадратов, каждый из которых имел разные значения вероятности, высокие и низкие, как на карте, показывающей вершины и долины с равными высотами. Крейвен выполнил первый шаг метода Байеса, как и рационалисты, определяющие, является ли девушка неженатой.

После этого Кравен вместе с командиром поисковой группы начал поиск снарядов, одновременно обновляя вероятности для каждой ячейки в процессе поиска. Однако наиболее вероятные места в ячейках часто указывают на труднодоступные ущелья на суше и глубокие морские районы, и даже если снаряды действительно там, их не обязательно можно найти, поэтому нужно нарисовать другую карту вероятности, показывающую, что снаряды уже там, а не вероятность расположения снарядов.

Всего через два года, в 1968 году, у Кравена появилась возможность проявить свой талант, и он снова потерял небольшую бомбу, но в этот раз ВМС США потеряли огромную бомбу.

В июне 1968 года в Атлантическом океане в Азовском море внезапно исчезла атомная подводная лодка “Свайн”, и 99 военно-морских офицеров и военнослужащих, находившихся на борту, были без вести. Согласно отчету о последующем расследовании, виновником трагедии была странная торнадо, которая была выпущена на подводной лодке, а после выстрела, повернувшаяся, выстрелила в себя, взорвав подводную лодку.

В поисках местонахождения “Светильника” военно-морские силы США провели масштабный поиск, в котором, естественно, участвовал и Крейвен. Из-за быстрого и медленного движения подводной лодки во время аварии, направление, направление силы взрыва, направление стрелки подводной лодки во время взрыва неизвестно, и даже если известно, где подводная лодка взорвалась, трудно определить, куда остатки подводной лодки были в конечном итоге затоплены.

Ни один эксперт не может точно оценить, что произошло с подводной лодкой до и после происшествия, и, как и в случае с поиском бомбы, Кравен консультировался с математиками, специалистами по подводным лодкам и специалистами в различных областях морского поиска, чтобы составить сценарии с различными возможными сценариями, позволяя им делать предположения о том, в каком направлении ситуация будет развиваться в соответствии с их знаниями и опытом.

В конце концов, Кравен получил карту вероятности 20-мильной морской зоны. Вся морская зона была разделена на множество подсетей, каждая из которых имела два значения вероятности p и q, p - вероятность того, что субмарина лежит в этой сетке, q - вероятность того, что она будет найдена, если субмарина находится в этой сетке.

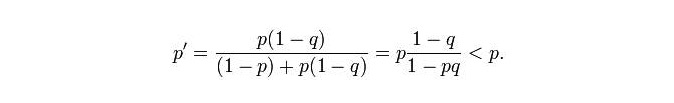
В этом случае вероятность существования подводных лодок в других ячейках возрастает:

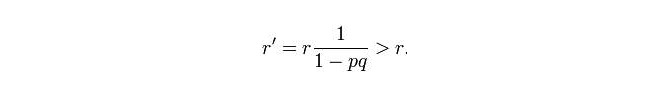
Каждый раз, когда подводные лодки входят в зону поиска, выбирают для поиска одну из сеток, в которой наибольшая вероятность существования подводных лодок, а если она не обнаружена, то распределение вероятности промывается один раз, и поисковые корабли отправляются в новую сетку, наиболее подозрительную для поиска, и так далее, пока не найдут щуку.

Первоначально военно-морские силовики, исходя из опыта, предположили, что подводная лодка находится на дне моря к востоку от места взрыва, что было довольно необоснованно для Кравена и других математиков, но после нескольких месяцев поисков ничего не было найдено. Впоследствии военно-морские силы были вынуждены прислушаться к совету Кравена, согласно вероятностному графику, потерпевшая катастрофу подводная лодка должна была находиться на западной стороне места взрыва. После нескольких поисков подводная лодка была найдена на дне моря к юго-западу от места взрыва.

После двух мощных демонстраций, метод Бейеса, используемый Кравеном в морском поиске, постепенно стал широко распространенным, и с тех пор метод Бейеса неожиданно стал повсеместным ключевым словом, часто встречающимся наряду с гидравлическими бомбами и ядерными подводными лодками. В течение десятилетий метод Бейеса применялся все шире и шире, от поисковой строки Google до автономного автомобиля, чтобы определить свое местоположение.

Снимок с сайта “Математическое моделирование”