Семь методов регрессии, которые вам следует освоить

**В этой статье объясняется регрессионный анализ и его преимущества, в основном резюмируются семь наиболее часто используемых регрессионных технологий и их ключевые элементы, такие как линейная регрессия, логическая регрессия, многополюсная регрессия, постепенная регрессия, контурная регрессия, регрессия на зацепке, регрессия ElasticNet, и, наконец, ключевые факторы выбора правильной модели регрессии. ** ** Анализ регрессии с помощью кнопок редактора является важным инструментом для моделирования и анализа данных. В этой статье объясняется смысл регрессионного анализа и его преимущества. В основном речь идет о семи наиболее часто используемых методах регрессии, таких как линейная регрессия, логическая регрессия, многополюсная регрессия, пошаговая регрессия, паутина регрессия, регрессия с зацеплением и регрессия ElasticNet, а также об их ключевых элементах, и, наконец, о ключевых элементах выбора правильной модели регрессии.**

• ### Что такое регрессионный анализ?

Регрессионный анализ - это метод прогнозирующего моделирования, изучающий взаимосвязь между коэффициентом (задачей) и коэффициентом (предсказателем). Этот метод обычно используется для прогнозного анализа, моделирования временных последовательностей и причинно-следственных связей между обнаруженными переменными. Например, лучший способ исследования взаимосвязи между безрассудным вождением водителей и количеством дорожно-транспортных происшествий - это регрессия.

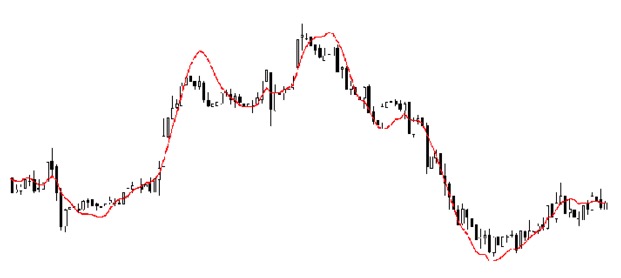
Регрессионный анализ является важным инструментом для моделирования и анализа данных. Здесь мы используем кривую/линию для сопоставления этих точек данных, таким образом, минимальная разница в расстоянии от кривой или линии до точки данных. Я объясню это подробно в следующей части.

• ### Почему мы используем регрессию?

Как уже говорилось выше, регрессионный анализ оценивает взаимосвязь между двумя или более переменными. Давайте приведем простой пример, чтобы понять это:

Например, в текущих экономических условиях вы хотите оценить рост продаж компании. Теперь у вас есть последние данные компании, которые показывают, что рост продаж примерно в 2,5 раза больше, чем рост экономики.

Использование регрессионного анализа имеет много преимуществ. В частности:

Она показывает существенную связь между самостоятельными и обусловленными переменными;

Она показывает, насколько сильно влияют несколько самоизменных на одну производящую переменную.

Регрессионный анализ также позволяет сравнивать взаимосвязи между переменными, которые измеряют различные масштабы, такие как связь между изменениями цен и количеством рекламных акций. Это помогает исследователям рынка, аналитикам данных и ученым по данным исключить и оценить оптимальный набор переменных для построения прогнозных моделей.

• ### Сколько у нас технологий регрессии?

Существует множество различных методов регрессии, используемых для прогнозирования. Основными из них являются три измерения: количество самоизменных, тип самоизменных и форма линий регрессии. Мы подробно рассмотрим их в следующих разделах.

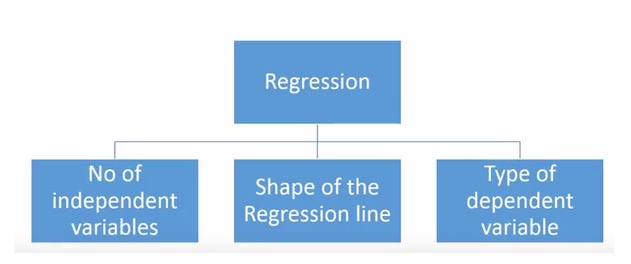
Для тех, кто изобретателен, можно даже создать неиспользованную модель регрессии, если вам кажется необходимым использовать комбинацию из вышеперечисленных параметров. Но прежде чем вы начнете, узнайте о наиболее часто используемых методах регрессии:

• 1. Линейная регрессия

  Это одна из наиболее известных методов моделирования. Линейное регрессирование обычно является одним из методов, избранных для изучения прогнозных моделей. В этой технике, поскольку переменные являются непрерывными, самоизменные могут быть непрерывными или дисперсными, характер линии регрессии является линейным.

  Линейная регрессия использует наилучшую совпадающую прямую ((т. е. регрессионную линию) для установления отношения между производной переменной ((Y) и одной или несколькими производной переменной ((X)).

  Это выражено в уравнении: y=a+b.*X + e, где a представляет собой сечение, b представляет собой наклон прямой линии, а e - погрешность. Это уравнение позволяет прогнозировать значение целевой переменной в зависимости от заданной прогнозной переменной (s).

  

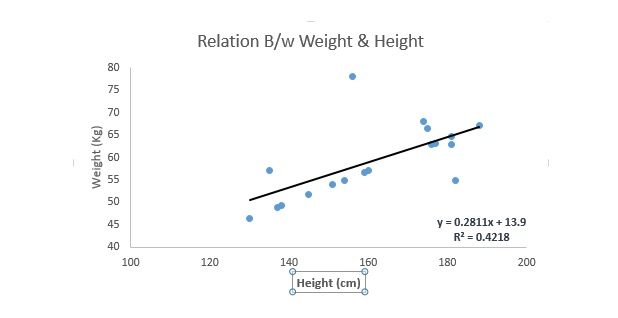
  Отличие однолинейной регрессии от многолинейной регрессии состоит в том, что многолинейная регрессия имеет ((>1) самостоятельную переменную, в то время как однолинейная регрессия обычно имеет только одну самостоятельную переменную. Теперь вопрос в том, как мы получим оптимальную линию соответствия?

  Как получить значение наилучшей линии сочетания (a и b)?

  Эту задачу можно легко выполнить с помощью наименьшего двоичного умножения. Наименьшее двоичное умножение также является наиболее часто используемым методом для сопоставления регрессионных линий. Для наблюдений он вычисляет наилучшую сопоставимую линию, минимизируя сумму квадратных вертикальных отклонений от линии каждой точки данных. Поскольку при сложении отклонения первые квадратные, положительные и отрицательные значения не компенсируются.

  

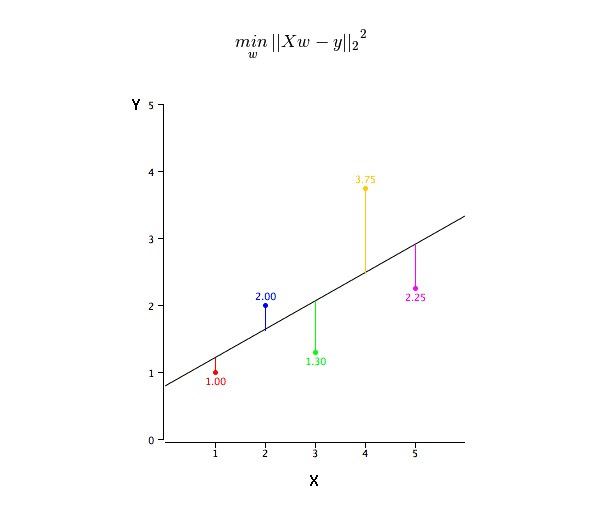
  Мы можем использовать R-квадратные показатели для оценки производительности моделей. Подробнее об этих показателях читайте: Показатели производительности моделей Part 1, Part 2 .

  Примечание:

  • Линейная взаимосвязь между самостоятельными и коэффициентными переменными
  • Множественная регрессия имеет множественную колинейность, корреляцию и дифференциальность.
  • Линейная регрессия очень чувствительна к аномальным значениям. Она может сильно повлиять на линию регрессии и в конечном итоге повлиять на прогнозные значения.
  • Множественная колинейность увеличивает дифференциацию коэффициентных оценок, что делает их очень чувствительными к незначительным изменениям модели. В результате коэффициентные оценки становятся неустойчивыми.
  • В случае с несколькими самоизменными мы можем выбрать наиболее важную самоизменную, используя метод выбора вперед, метод удаления вперед и метод поэтапного отбора.

• 2. Logistic Regression логическая регрессия

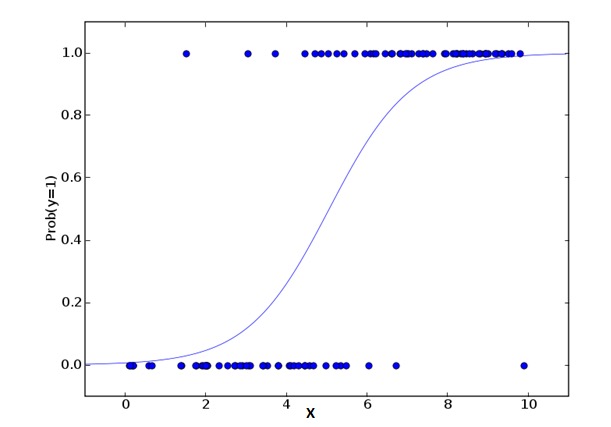
  Логическая регрессия используется для вычисления вероятности совпадения событий Success и Failure. Мы должны использовать логическую регрессию, когда тип переменной относится к двоичной переменной ((¹⁄₀, true/false, yes/no). Здесь значение Y от 0 до 1, которое может быть выражено следующим уравнением:

  odds= p/ (1-p) = probability of event occurrence / probability of not event occurrence
  ln(odds) = ln(p/(1-p))
  logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3....+bkXk
  

  В приведенных выше формулах p обозначает вероятность того, что оно имеет какую-то особенность. Вы должны задать вопрос: почему мы используем логические числа в формулах?

  Поскольку здесь мы используем двоичное распределение ((из переменной), нам нужно выбрать связующую функцию, наиболее подходящую для этого распределения. Это функция Logit. В вышеуказанном уравнении параметры выбираются путем оценки величины наибольшей вероятности наблюдения за образцом, а не путем минимизации квадрата и погрешности (как в обычной регрессии).

  

  Примечание:

  • Он широко используется для классификации.
  • Логическая регрессия не требует линейных отношений между самостоятельными и конечными переменными. Она может обрабатывать различные типы отношений, поскольку она использует нелинейную логическую преобразование относительно прогнозируемого ОРИ.
  • Чтобы избежать пересоответствия и несоответствия, мы должны включать все важные переменные. Есть хороший способ обеспечить это, используя методы поэтапного отбора для оценки логической регрессии.
  • Он требует большого количества образцов, поскольку при небольшом количестве образцов высокая вероятность оценки эффекта хуже, чем обычный минимальный коэффициент.
  • Самостоятельные переменные не должны быть взаимосвязаны, то есть не имеют множественной колониальности. Однако, в анализе и моделировании мы можем выбрать, чтобы включать влияние взаимодействия классифицируемых переменных.
  • Если значение переменной зависимости является последовательной переменной, то она называется последовательной логической регрессией.
  • Если переменная является многообразной, то она называется многообразной логической регрессией.

• 3. Полиномиальная регрессия

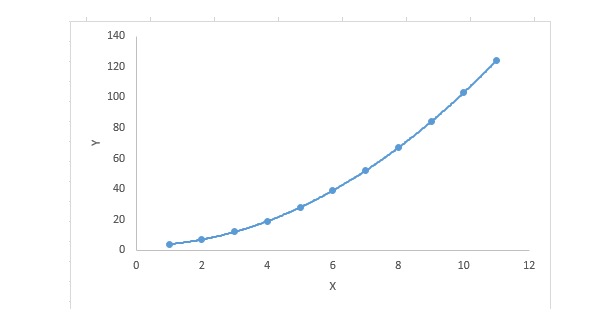
  Для регрессивного уравнения, если индекс самой переменной больше 1, то оно является многополюсным регрессивным уравнением.

  y=a+b*x^2
  

  В этой регрессионной технике оптимальная линия соответствия не является прямой, а является кривой, используемой для соответствия точек данных.

  

  Основные моменты:

  • Несмотря на то, что существует индукция, позволяющая сопоставить высокоуровневый полиметрический выражение и получить меньшую ошибку, это может привести к пересогласованности. Вам нужно регулярно рисовать диаграммы отношений, чтобы проверить соответствие, и сосредоточиться на том, чтобы убедиться, что соответствие является обоснованным и не является ни пересогласованным, ни недосогласованным. Ниже приведен пример, который поможет понять:

  

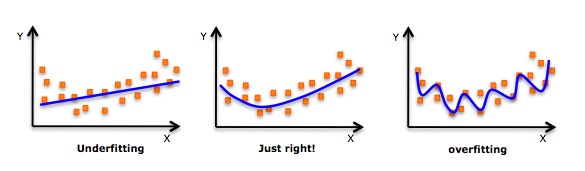
  • Очевидно, что нужно искать точки кривой на обоих концах, чтобы увидеть, имеют ли смысл эти формы и тенденции. Высокоуровневые полиномы могут в конечном итоге привести к странным выводам.

• 4. Пошаговая регрессия

  При обработке нескольких самовариантов мы можем использовать эту форму регрессии. В этой технике выбор самовариантов выполняется в автоматическом процессе, включающем нечеловеческие действия.

  Этот подвиг заключается в том, чтобы идентифицировать важные переменные, наблюдая за статистическими значениями, такими как R-square, t-stats и AIC. Постепенная регрессия приспосабливается к модели путем одновременного добавления/удаления коэффициентов, основанных на заданных критериях. Ниже перечислены некоторые из наиболее часто используемых методов поэтапной регрессии:

  • Стандартная пошаговая регрессия делает две вещи: добавляет и удаляет прогнозы, необходимые для каждого шага.
  • Продвигающийся подход начинается с наиболее заметных прогнозов модели, а затем добавляет переменные для каждого шага.
  • Метод удаления заднего ряда начинается одновременно со всеми прогнозами модели, а затем на каждом этапе устраняется наименее значимая переменная.
  • Целью этой моделирования является использование наименьшего количества прогнозных переменных для максимизации прогнозной способности. Это также один из способов обработки высокомерных наборов данных.

• 5. Регрессионный ридж

  Гиперрегрессионный анализ - это технология, используемая при наличии данных с множественной комолинейностью (высокой корреляцией с переменной). В случае с множественной комолинейностью, хотя минимальное двоичное умножение (OLS) является справедливым для каждой переменной, их различия настолько велики, что наблюдаемые значения смещаются и удаляются от истинных значений. Гиперрегрессионный анализ снижает стандартную ошибку, добавляя одно из отклонений к оценке возврата.

  Выше мы видели линейную регрессию.

  y=a+ b*x
  

  Это уравнение также имеет элемент погрешности.

  y=a+b*x+e (error term),  [error term is the value needed to correct for a prediction error between the observed and predicted value]
  => y=a+y= a+ b1x1+ b2x2+....+e, for multiple independent variables.
  

  В линейном уравнении ошибка прогноза может быть разбита на 2 поддобавки. Одна - отклонение, другая - дифференциал. Ошибка прогноза может быть вызвана этими двумя добавками или любой из них. Здесь мы поговорим об ошибках, вызванных дифференциалом.

  Глубокая регрессия решает множественную комолинейную задачу с помощью сжатого параметра λ{\displaystyle \lambda } . См. формулу ниже

  

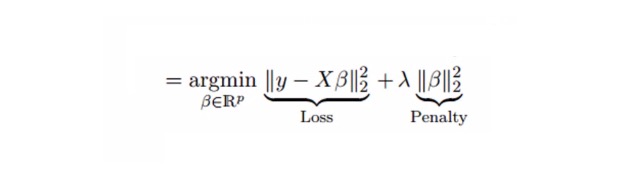
  В этой формуле имеются две составляющие. Первая - наименьшее двоичное число, другая - кратность λ β2 ((β-квадрат), где β является соответствующим коэффициентом. Для уменьшения параметров добавьте его к наименьшему двоичному числу, чтобы получить очень низкий дифференциал.

  Примечание:

  • Помимо константы, такая регрессия предполагается аналогично регрессии наименьшего двоичного числа;
  • Он уменьшает значение соответствующего коэффициента, но не достигает нуля, что указывает на отсутствие функции выбора признаков
  • Это метод регуляризации, и используется регуляризация L2.

• 6. Лассо регрессия

  Он похож на гибридный регресс, а Lasso (Least Absolute Shrinkage and Selection Operator) также наказывает за абсолютный размер коэффициента регрессии. Кроме того, он способен уменьшить степень изменения и повысить точность линейной регрессионной модели.

  

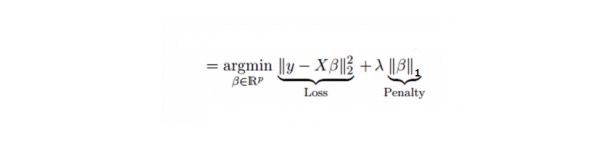
  Лассо-регрессия немного отличается от Ридж-регрессии тем, что использует функцию наказания, которая является абсолютной, а не квадратной. Это приводит к тому, что наказание (или сумма абсолютных значений, равная обязывающей оценке) приводит к тому, что некоторые параметры оценочного результата равны нулю. Чем больше значение наказания используется, тем больше дальнейшая оценка приближает сокращенное значение к нулю. Это приводит к тому, что мы выбираем переменную из данных n переменных.

  Примечание:

  • Помимо константы, такая регрессия предполагается аналогично регрессии наименьшего двоичного числа;
  • Его коэффициент сжатия приближается к нулю, что действительно помогает в выборе признаков;
  • Это метод регуляризации с использованием L1 регуляризации.
  • Если прогнозируемый набор переменных является высокосвязанным, Лассо выбирает один из них и сворачивает остальные до нуля.

• 7. Возвращение ElasticNet

  ElasticNet является гибридом технологий регрессии Лассо и Риджа. Он использует L1 для обучения и L2 в качестве приоритетной матрицы для нормализации. ElasticNet полезен, когда есть несколько связанных признаков.

  

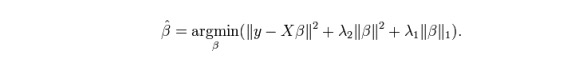
  Фактическое преимущество между Lasso и Ridge заключается в том, что это позволяет ElasticNet унаследовать некоторую стабильность Ridge в циклическом состоянии.

  Примечание:

  • В случае с высоко коррелирующими переменными, это создает групповой эффект.
  • Количество выбранных вариантов не ограничено.
  • Она выдерживает двойную сжатие.
  • В дополнение к этим семи наиболее часто используемым методам регрессии вы можете посмотреть на другие модели, такие как байесовская, экологическая и робустная регрессия.

• Как правильно выбрать модель регрессии?

  Жизнь обычно проще, когда вы знаете только одну или две техники. Я знаю одну учебную организацию, которая сказала своим студентам, что если результат непрерывный, то используйте линейную регрессию. Если двоичный, то используйте логическую регрессию! Однако, чем больше вариантов в нашей обработке, тем труднее выбрать правильный.

  В многообразной регрессионной модели очень важно выбрать наиболее подходящую технологию на основе типа самостоятельных и произвольных переменных, измерений данных и других основных характеристик данных. Вот ключевые факторы, которые помогут вам выбрать правильную регрессионную модель:

  Изучение данных является неотъемлемой частью построения прогнозных моделей. Это должен быть первоочередной шаг при выборе подходящей модели, например, для выявления взаимосвязей и влияния переменных.

  Для сравнения преимуществ различных моделей мы можем анализировать различные показательные параметры, такие как параметры статистической значимости, R-square, Adjusted R-square, AIC, BIC, а также элементы погрешности. Другой является Mallows’ Cp rule. Это в основном происходит путем сравнения модели со всеми возможными подмоделями (или их тщательного выбора) и проверки возможных отклонений в вашей модели.

  Кроссовка является наиболее эффективным способом оценки прогнозной модели. Здесь вы делите свой набор данных на две части (одна для тренировки, другая для проверки) и используете простую уравнительную разницу между наблюдаемым и прогнозируемым значением для измерения точности вашего прогноза.

  Если ваш набор данных состоит из нескольких смешанных переменных, то вы не должны использовать метод автоматического выбора модели, потому что вы не хотите, чтобы все переменные находились в одной модели одновременно.

  Это также будет зависеть от ваших целей. Может возникнуть ситуация, когда менее мощная модель будет более легко реализована, чем модель с высокой статистической значимостью.

  Методы регрессионной нормализации ((Lasso, Ridge и ElasticNet) хорошо работают в условиях многократной комолинейности между высокими измерениями и переменными набора данных.

Продолжение из CSDN