Интересное понимание наивного байесовского алгоритма

NavieBayes

  В жизни существует множество случаев, когда классификация требуется, например, для классификации новостей, классификации пациентов и т. д. Для того, чтобы вы могли представить себе это, в этой статье представлен простой, широко используемый классификационный алгоритм, начиная с практического применения - простой Бейес (Navie Bayes classifier).

• 01 Пример классификации пациентов

Позвольте мне начать с примера, и вы увидите, что классификатор Bayes понятен, и это не сложно. Одна больница приняла шесть пациентов на прием утром, как показано в таблице ниже.

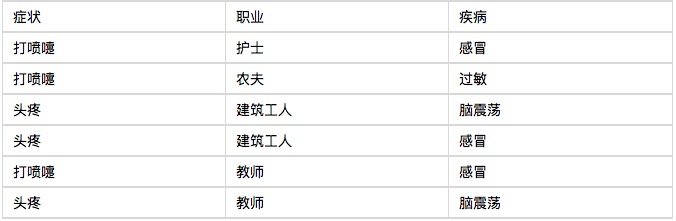
Теперь приходит седьмой пациент, строительный рабочий, который чихает. Спросите, какая вероятность того, что он простудится?

  P(A|B) = P(B|A) P(A) / P(B)

Вполне возможно:

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏x建筑工人|感冒) x P(感冒) 
  　　　　/ P(打喷嚏x建筑工人)

Предположим, что эти два признака - “пыркающий” и “строительный работник” - независимы, и, следовательно, вышеупомянутое уравнение становится

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒)
  　　　　/ P(打喷嚏) x P(建筑工人)

Это можно рассчитать.

  P(感冒|打喷嚏x建筑工人) 
  　　　　= 0.66 x 0.33 x 0.5 / 0.5 x 0.33 
  　　　　= 0.66

Таким образом, вероятность того, что строительный работник, который чихнул, заболел простудой, составляет 66%. Таким же образом, можно рассчитать вероятность того, что пациент страдает аллергией или сотрясением мозга. Сравнивая эти вероятности, можно узнать, какая болезнь наиболее вероятна для него.

Это и есть основной метод классификатора Байеса: на основе статистических данных, исходя из определенных характеристик, рассчитывается вероятность каждой категории, чтобы осуществить классификацию.

• 02 Формулы простого классификатора Бейса

Предположим, что у индивида есть n характеристик, F1, F2, … , Fn. Существует m категорий, C1, C2, … , Cm. Классификатор Байеса - это классификация, которая рассчитывает наибольшую вероятность, то есть максимальное значение следующего алгоритма:

  P(C|F1F2...Fn) 
  　　   = P(F1F2...Fn|C)P(C) / P(F1F2...Fn)

Поскольку P ((F1F2…Fn) одинаковы для всех категорий, их можно пропустить, и вопрос становится простым.

  P(F1F2...Fn|C)P(C)

Максимальное значение

Простая классификаторная классификаторная классификаторная классификаторная классификаторная классификаторная классификаторная классификаторная классификаторная классификаторная классификаторная классификаторная классификаторная классификаторная классификаторная классификаторная классификаторная классификаторная классификаторная классификаторная классификаторная классификация

  P(F1F2...Fn|C)P(C) 
  　　   = P(F1|C)P(F2|C) ... P(Fn|C)P(C)

Каждый элемент в правой части эквивалента может быть получен из статистических данных, из которых можно вычислить вероятность соответствия каждой категории, чтобы найти наиболее вероятную категорию.

Хотя гипотеза о том, что “все признаки независимы друг от друга”, вряд ли будет работать в реальности, она значительно упрощает расчет, и есть исследования, которые показывают, что это не влияет на точность результатов классификации.

Далее приведем два примера, как можно использовать примитивный классификатор Bayes.

• 03 Классификация аккаунтов

Согласно выборочной статистике одного из сайтов сообщества, 89% из 10000 аккаунтов на этом сайте являются реальными (установить C0), а 11% - фальшивыми (установить C1). Следующее, что нужно сделать, это использовать статистику для оценки подлинности аккаунта.

  C0 = 0.89 C1 = 0.11

Предположим, что учетная запись имеет три характеристики: F1: Количество дневников / число дней регистрации F2: Количество друзей / число дней регистрации F3: Используются ли реальные заголовки (например, реальные заголовки - 1, недействительные заголовки - 0) F1 = 0.1  F2 = 0.2  F3 = 0

Просьба, укажите, настоящий счет или поддельный? Метод состоит в том, чтобы использовать простой Bayesian классификатор и вычислить значение следующей формулы:

P(F1|C)P(F2|C)P(F3|C)P©

Хотя вышеперечисленные значения можно получить из статистических данных, однако здесь возникает проблема: F1 и F2 являются непрерывными переменными и не подходят для вычисления вероятности в зависимости от какого-либо конкретного значения.[0, 0.05]、(0.05, 0.2)、[0.2, +∞] три диапазона, а затем вычислить вероятность каждого диапазона. В нашем примере F1 равен 0.1, попавшему во второй диапазон, поэтому при вычислении используется вероятность наступления второго диапазона.

Согласно статистическим данным:

P(F1|C0) = 0.5, P(F1|C1) = 0.1  P(F2|C0) = 0.7, P(F2|C1) = 0.2  P(F3|C0) = 0.2, P(F3|C1) = 0.9

Поэтому

P(F1|C0) P(F2|C0) P(F3|C0) P(C0)  = 0.5 x 0.7 x 0.2 x 0.89  = 0.0623 P(F1|C1) P(F2|C1) P(F3|C1) P(C1)  = 0.1 x 0.2 x 0.9 x 0.11  = 0.00198 Можно увидеть, что, хотя пользователь не использовал подлинный профиль, вероятность того, что он является подлинным аккаунтом, более чем в 30 раз выше, чем вероятность использования поддельного аккаунта, и, следовательно, можно судить, что этот аккаунт является подлинным.

• 04 Сексуальная классификация

Ниже приведены статистические данные о группе характеристик человеческого тела.

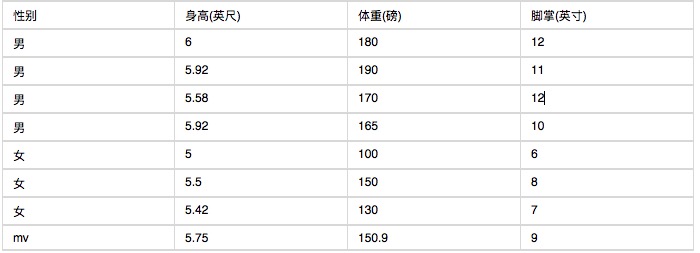
Известно ли, что человек ростом 6 футов, весом 130 фунтов, с ладонями 8 дюймов, является ли он мужчиной или женщиной?

P (рост и пол) x P (вес и пол) x P (рост и пол) x P (рост и пол)

Сложность заключается в том, что, поскольку рост, вес и ладони являются непрерывными переменными, вероятность не может быть рассчитана с помощью метода дифференцированных переменных. И, поскольку выборка слишком мала, она не может быть разделена на промежуточные вычисления. Что делать?

Эти данные позволяют рассчитать классификацию по полу.

P (высота = 6 человек) x P (вес = 130 человек) x P (площадь ног = 8 человек) x P (мужчина)

= 6.1984 x e-9

P (высота = 6 девушек) x P (вес = 130 девушек) x P (площадь ног = 8 девушек) x P (женщина)

= 5.3778 x e-4

Как видно, вероятность того, что это будет женщина, почти в 10 000 раз выше, чем вероятность того, что это будет мужчина.

Общественный номер Weibo, опубликованный на сайте Weibo.