Интуитивное понимание коинтеграции

Введение: В данной статье предлагается визуально представить концепцию интеграции, чтобы помочь вам понять ее основные значения, мотивы, которые приводят к концепции, и простые сценарии ее применения.

• Описание

Я просто хочу указать на то, что понятие целостности имеет интуитивное определение и не включает в себя строгие математические обозначения и формулы.

Если вы заинтересованы, то обратитесь к Википедии Cointegration.

Почему нужно быть сплоченным?

Когда речь заходит о сплоченности, то приходится говорить о равновесии.

Проще говоря, стационарность (англ. stationarity) - это свойство последовательности, которое сохраняет стабильность во времени, и это свойство нам очень нравится при аналитических прогнозах данных. Если набор данных временной последовательности является стабильным, это означает, что его средние и дифференциальные значения остаются неизменными, и мы можем легко использовать некоторые статистические методы для последовательности.

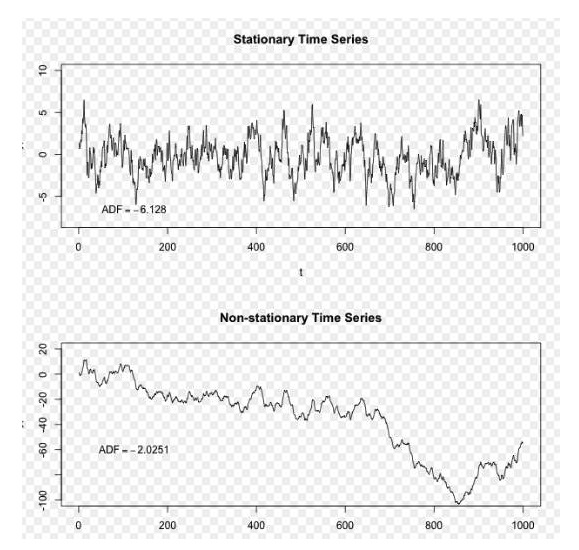
Изображение: Википедия

В приведенном выше рисунке верхняя последовательность является устойчивой, и мы видим, что она всегда колеблется вокруг долгосрочного среднего значения, а нижняя последовательность является неустойчивой, и мы видим, что ее долгосрочное среднее значение изменяется.

В качестве примера применения, если ценовая последовательность какого-либо актива (или цена между двумя последовательностями) является устойчивой, то, когда она отклоняется от средней стоимости, можно ожидать, что цена в будущем вернется к этой средней стоимости. Мы можем использовать это свойство для инвестирования, чтобы получить прибыль. Предположим, что долгосрочная средняя стоимость одной акции составляет 9 долларов, а ее нынешняя стоимость составляет 8 долларов.

Вот последовательность цен на акции, имеющая устойчивый характер:

Если две группы последовательностей не являются равномерными, но их линейная комбинация может дать равномерную последовательность, то мы можем сказать, что эти две группы данных временной последовательности обладают целостными свойствами, и мы также можем применить статистические свойства к этой комбинации. Но следует отметить, что целостная связь не является корреляцией.

Например, если разница между двумя группами данных временной серии является равномерной, то мы можем инвестировать в прибыль в соответствии с равномерностью разницы: когда цена двух акций слишком велика, в соответствии с равномерностью мы ожидаем, что разница в цене будет сокращаться, поэтому покупаем акции с низкой ценой, продаем акции с высокой ценой и ждем, пока цена вернется, чтобы получить прибыль.

Это и есть суть торговли парами.

• Стабильность и методы испытаний

Строго говоря, устойчивость может быть разделена на строго стационарную и слабую стационарную. Строго стационарная означает, что последовательность всегда имеет неизменную функцию распределения, а слабая - описательную статистическую величину постоянной величины последовательности. Все сильные и устойчивые последовательности удовлетворяют свойству слабой устойчивости, но наоборот.

Пример приложения

В первую очередь следует отметить, что корреляция не является корреляцией. Мы искусственно сконструировали две группы данных, чтобы визуализировать корреляцию. import numpy as np import pandas as pd import seaborn import statsmodels import matplotlib.pyplot as plt from statsmodels.tsa.stattools import coint

Конструктивные данные

Во-первых, мы построили две группы данных, каждая из которых имеет длину 100. Первая группа данных содержит 100 плюс один элемент нисходящего тренда, плюс стандартное нормальное распределение. Вторая группа данных основана на первой группе данных, плюс 30, плюс дополнительное стандартное нормальное распределение.

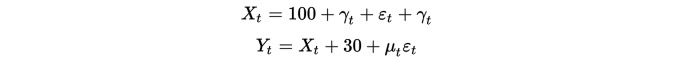
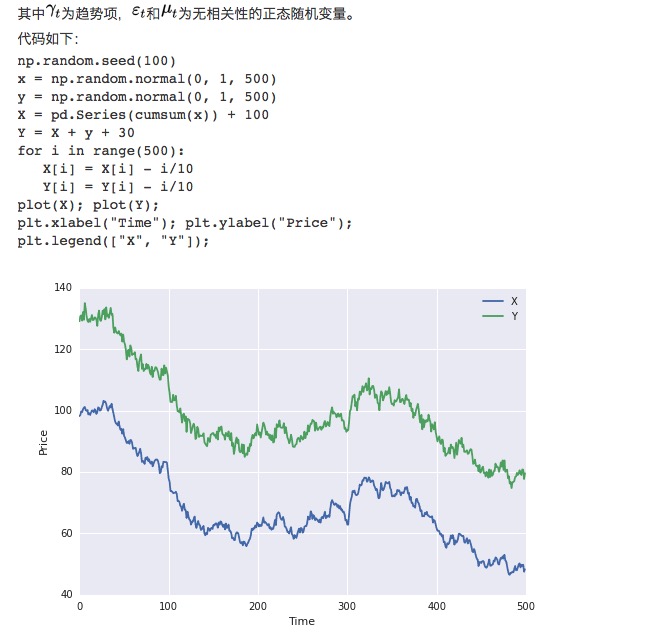
Очевидно, что эти две группы данных являются неравномерными, поскольку средние значения изменяются с изменением времени. Но эти две группы данных имеют интегральную связь, поскольку их дифференциальная последовательность является равномерной:

plot(Y-X); plt.axhline((Y-X).mean(),color=“red”, linestyle=“–”); plt.xlabel(“Time”); plt.ylabel(“Price”); plt.legend([“Y-X”, “Mean”]);

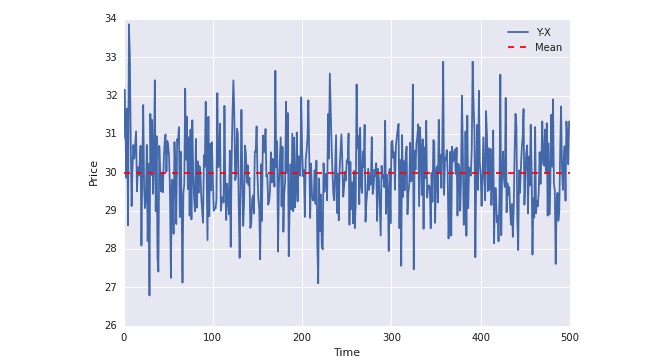
На рисунке выше видно, что синяя линия постоянно колеблется вокруг среднего значения. Среднее значение не изменяется со временем.

• Заключение

Если объединение будет рассматриваться с математической точки зрения, то это будет сложнее, и в будущем это будет затронуто в уроках количественной оценки. Мы просто делаем простое введение на уровне понимания (уровня-0), чтобы лучше объединить объединение с практическим применением.

Я хочу поделиться своим опытом с другими.