Юань Риккиё, Юань Сюй Чжунь, Юань Мовер и кривая богов

В предыдущем выпуске говорилось, что Якоб Бернули умер, не опубликовав свою книжную теорию гипотетики о теории вероятности. Работу над его рукописью поручили его племяннику Николаю II Бернули (именно тому гениальному утром). После исполнения завещания своего дяди, Николас снова начал искать уровень отклонения от истинной вероятности при условии, что было определено количество наблюдений. В некоторых местах “Авраам де Моивр” переводится как “Авраам Моивр”, но после просмотра его портрета я не очень-то согласен с последующим переводом. Это приглашение могло бы стать поводом для последнего поэтического поцелуя, но Моивр отказался. Причиной его отказа стало то, что он не считал себя достаточно сильным.

• Деммовер Позже французский король Людовик XIV издал указ, объявляющий местных протестантов низшими гражданами, и дети должны были обратиться в протестантство. Этот закон в основном сделал протестантство культовым в Франции, и по этой причине он провёл два года в тюрьме. После освобождения из тюрьмы, Монро пытался бежать в Англию, но он не получил преподавательской должности в академическом мире, несмотря на то, что он был другом Ньютона, и несмотря на то, что он был членом британской королевской семьи в возрасте 30 лет.

В 1711 году Том Мовер опубликовал басню о измерении удачи, на которой, если бы она была напечатана в то время, наверняка была бы написана рекомендация Ньютона: “Спроси мистера Том Мофера, он знает об этом больше, чем я”.

К сожалению, в то время этого не было, и поэтому Том Мовер не смог получить столько налога на авторские права.

Вы, наверное, помните, что в нашей предыдущей статье мы задали вопрос: “Рисковая история” (III): Рядовой Бернулли: для 5000 каменных глыб в ящике мы можем произвести 25500 попыток, чтобы оценить пропорцию общего количества каменных глыб. Но вы также должны обнаружить, что 25500 повторных попыток - это слишком много, и лучше всего выбросить камень на один номер.

Используя методы алгебры и Паскальского треугольника, Монмовер использовал методы групповой выборки. Он предположил, что каждый раз вынимая из ящика 100 керамических камней, записывает пропорции черно-белых керамических камней, а затем кладет их обратно, а затем делает тот же выбор.

Да, это нормальное распределение, с которым мы все знакомы. Кривая нормального распределения похожа на колокольную кривую, где большинство наблюдений сосредоточено в центре, близко к среднему значению всех наблюдений, а затем из среднего значения наклоняется симметрично к обеим концам, и количество наблюдений на обеих концах среднего значения одинаково. Вначале кривая наклонена в быстром направлении, а на обеих концах такая наклонность становится плоской, что означает, что вероятность появления наблюдений, находящихся дальше от среднего значения, меньше.

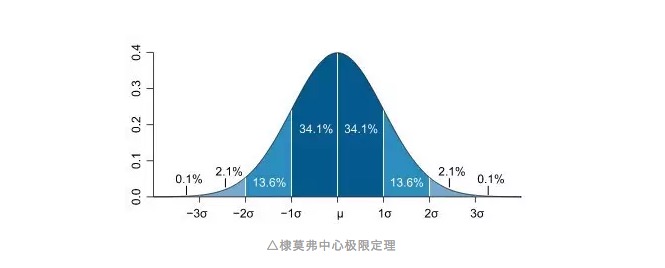
Таким образом, мы можем ввести понятие стандартного отклонения, о котором мы уже упоминали в других статьях в “Общественном номере”: “Почему стандартное отклонение? Измерение риска в глазах Бога”? Стандартное отклонение на самом деле описывает степень отклонения наблюдаемого значения от среднего значения, или мы понимаем его как единицу отклонения от среднего значения.

Будучи набожным человеком, Дюмовер считал, что часовые кривые - это творение Бога. По его мнению, с помощью таких измерений мы можем преодолеть неопределенность и, следовательно, победить все риски, поскольку на кривых уже описаны все возможные явления и их вероятности, возможно, из-за случайности возникают так называемые отклонения, но с течением времени эти отклонения больше не влияют на закон, который мы подводим.

В средней школе есть еще классический предмет (((Ой, почему я всегда использую предмет средней школы)) о пропускной способности продукции. Если для партии продукции, отраслевые стандарты считают, что уровень отходов не превышает 0,1%, это означает, что мы случайно выбираем 10000 из продукции, из которых, если отходов не более 10, то они проходят. Но в результате из этих 10000 в конечном итоге появляются 12, если в среднем уровень отходов продукции составляет 0,1%, фактически мы можем использовать метод Вэн Мофора, чтобы рассчитать, какова вероятность появления 12 отходов.

Но в большинстве случаев этот вопрос не имеет для нас никакого смысла. Поскольку мы, возможно, не знаем, каков будет средний уровень отходов в продуктах, то каковы шансы, что наша партия продуктов пройдет проверку, если средний уровень отходов выше, чем стандартный? Если взять 20 000 продуктов для тестирования, то результаты 10 000 продуктов могут быть получены для прямого использования?

Копировано из Китайского института количественных инвестиций