Опорные векторные машины в мозге

Поддержка векторной машины (SVM) является важным классификатором машинного обучения, который умело использует нелинейные преобразования, чтобы проецировать низкомерные характеристики в высокое измерение и выполнять более сложные классификационные задачи. SWM, похоже, использует математический трюк, который, как оказалось, соответствует механизму кодирования мозга. Название статьи: The importance of mixed selectivity in complex cognitive tasks (by Omri Barak al. ) (англ. The importance of mixed selectivity in complex cognitive tasks (by Omri Barak al. )) (англ. The importance of mixed selectivity in complex cognitive tasks (by Omri Barak al. ) (англ. The importance of mixed selectivity in complex cognitive tasks (by Omri Barak al. ) (англ. The importance of mixed selectivity in complex cognitive tasks) (англ. The importance of mixed selectivity in complex cognitive tasks (by Omri Barak al.))

• #### SVM

Сначала мы поговорим о сути нейронного кодирования: животные принимают определенный сигнал и ведут себя в соответствии с ним, один из них - преобразование внешнего сигнала в нейроэлектрический сигнал, другой - преобразование нейроэлектрического сигнала в сигнал принятия решения, первый процесс называется кодированием, а второй - декодированием. Истинная цель нейронного кодирования - это декодирование, а затем принятие решения. Поэтому, используя визуальное декодирование машинного обучения, самый простой способ сделать это - посмотреть на классификатор, даже на линейный классификатор логистической модели, чтобы отнести входящий сигнал к определенной классификации по определенным характеристикам.

Итак, давайте посмотрим, как происходит нейронное кодирование. Во-первых, нейрон можно рассматривать как RC-схему, регулирующую сопротивление и емкость в зависимости от внешнего напряжения. Когда внешний сигнал достаточно велик, он будет направлен, а в противном случае - закрыт.

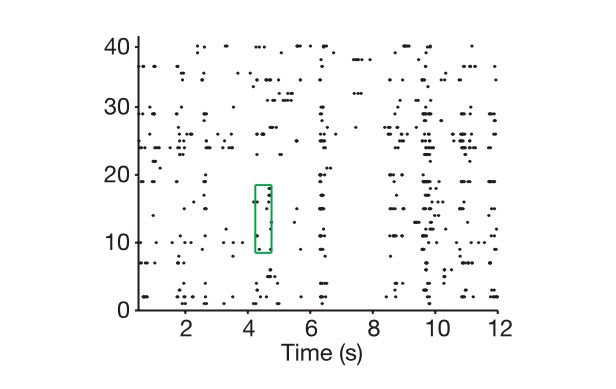
На диаграмме - клетки, на горизонтальной - время, и это показывает, как мы извлекаем нейронный код.

Конечно, существует разница между истинными измерениями N-мерного вектора и нейронного кода, и как определить истинные измерения нейронного кода? Во-первых, мы входим в N-мерное пространство, обозначенное этим N-мерным вектором, затем мы даем все возможные комбинации задач, например, показываем вам тысячу изображений, предполагая, что эти изображения представляют весь мир, обозначая каждый полученный нами нейронный код как точку в этом пространстве, и, наконец, мы используем мышление векторной алгебры, чтобы посмотреть на измерения подпространства, составляющие тысячу точек, то есть на истинные измерения нейронной символики.

В дополнение к кодированию, мы имеем понятие о реальном измерении внешнего сигнала, который представляет собой внешний сигнал, выраженный нейронной сетью, и, конечно, мы должны повторить все детали внешнего сигнала. Это бесконечная проблема, но основой для нашей классификации и принятия решений всегда были ключевые характеристики, процесс уменьшения измерений, это и есть идея PCA. Здесь мы можем рассматривать ключевые переменные в реальной задаче как реальное измерение задачи, например, если вы хотите управлять движением руки, вам обычно нужно только контролировать угол вращения сустава, и если вы используете это в качестве задачи физической механики, то размерность, вероятно, не будет выше десяти, мы называем это K. Даже если это проблема распознавания человеческого лица, размерность задачи все равно будет намного ниже, чем количество отдельных нейронов.

И тогда ученые сталкиваются с ключевой проблемой: почему они пытаются решить эту проблему с помощью кодирования и количества нейронов, которые намного больше, чем реальная проблема?

А вычислительная нейробиология и машинное обучение вместе говорят нам о том, что высокомерные свойства нейронных обозначений являются основой для их высокой способности к обучению. Чем выше измерение кодирования, тем выше способность к обучению. Обратите внимание, что мы даже не начинаем с глубинных сетей.

Обратите внимание, что нейронное кодирование, обсуждаемое здесь, в основном относится к нейронному кодированию высших нервных центров, таких как префронтальная кортекс (PFC), о котором говорится в статье, поскольку законы кодирования низших нервных центров не так сильно связаны с классификацией и принятием решений.

Высокие участки мозга, представленные PFC

Во-первых, мы предполагаем, что при использовании линейного классификатора мы не сможем решить нелинейную классификационную проблему, когда наша кодируемая величина равна величине ключевой переменной в реальной задаче (предположим, что вы хотите отделить кавуна от кавуна, но вы не можете выделить кавуна от кавуна с помощью линейной границы), и это типичная проблема, которую мы не смогли бы решить, когда глубокое обучение и SVM не вошли в машинное обучение.

SVM ((поддерживает векторные машины):

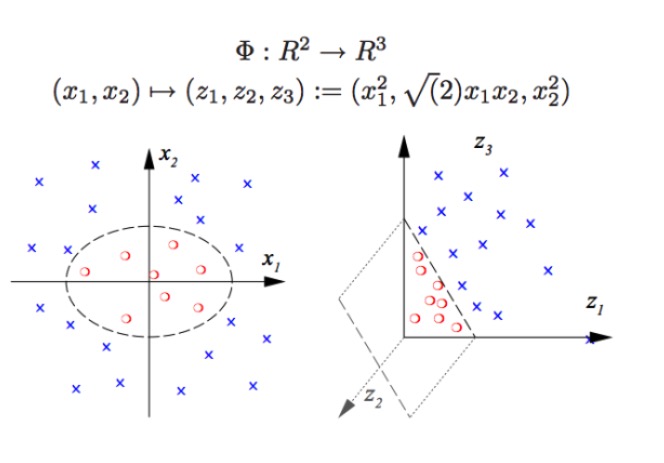
SVM может проводить нелинейную классификацию, например, разделить красные и синие точки на графике, с помощью линейных границ мы не можем разделить красные и синие точки (рисунок слева), поэтому метод SVM - увеличение измерения. Вместо того, чтобы просто увеличивать число переменных, это невозможно, например, отобразить (x1, x2) в (x1, x2, x1 + x2) система на самом деле является двумерным линейным пространством (нарисовать линию означает, что красные и синие точки находятся в одной плоскости), используя только нелинейные функции (x1 ^ 2, x1)*x2, x2^2) мы получили существенный переход от низкого к высокому измерению, когда вы бросаете голубую точку в воздух, а затем вы рисуете плоскость в воздухе, отделяющую голубую точку от красной, как показано на рисунке справа.

На самом деле, то, что делают настоящие нейронные сети, очень похоже на это. Такой линейный классификатор (декодер) может проводить значительное увеличение видов классификации, то есть мы получаем гораздо более мощную способность распознавать модели, чем раньше. Здесь высокое измерение - это высокая энергия, высокое измерение - это правда.

Как же получить высокое измерение нейронного кода? Большое количество фотонейронов бесполезно. Поскольку мы знаем из линейной алгебры, что если у нас есть огромное количество N нейронов, и скорость выброса каждого из них линейно связана только с K ключевой характеристикой, то измерение, которое мы в конечном итоге охарактеризуем, будет равняться измерению самого вопроса, а ваши N нейронов не будут иметь никакого значения (все выделяемые нейроны являются линейной комбинацией K нейронов).

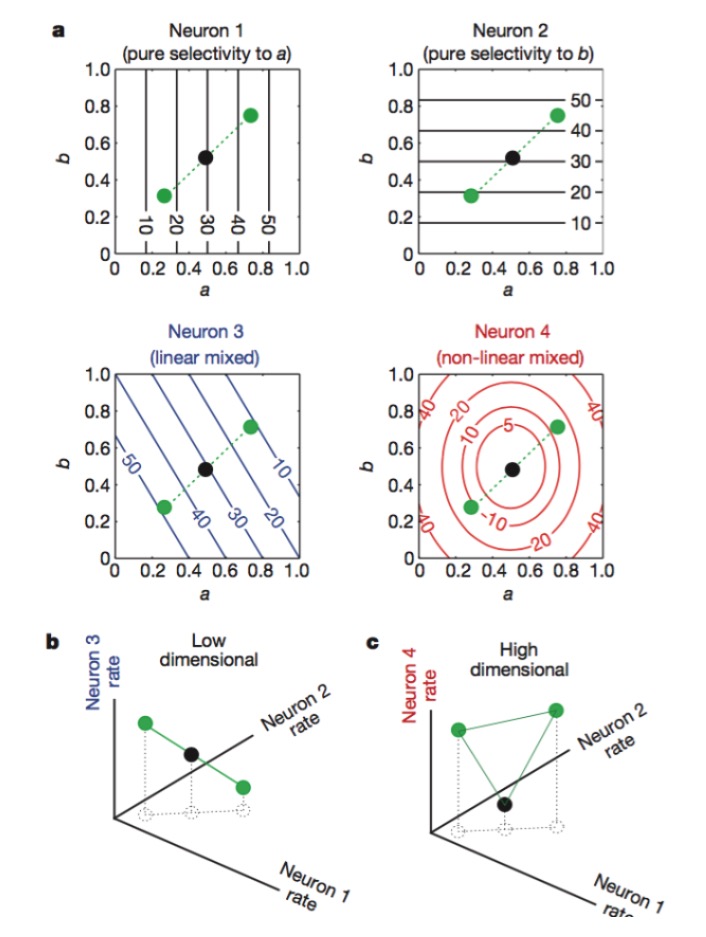
Рисунок: нейроны 1 и 2 чувствительны только к признакам a и b, 3 - к линейной смеси признаков a и b, а 4 - к нелинейной смеси признаков. В конечном итоге только комбинация нейронов 1, 2, 4 повышает размер нейрокодирования (рисунок ниже).

В окружающей нервной системе нейроны действуют как датчики, извлекающие и распознающие различные признаки сигналов. Функции каждой нервной клетки довольно специфичны, например, роды и конусы в сетчатке зрения отвечают за прием фотонов, а затем продолжает кодировать Gangelion cell, и каждый нейрон похож на специально обученного стражника. В более высоких областях мозга, где эта четкая разметка затрудняется, мы обнаруживаем, что одна и та же нервная клетка может быть чувствительна к различным признакам, и эта чувствительность не является линейной.

Каждая деталь природы содержит в себе приставку, большое количество избыточностей и смешанное кодирование, это выглядит не профессионально, выглядит как беспорядочный сигнал, в конечном итоге получается лучшая вычислительная мощность.

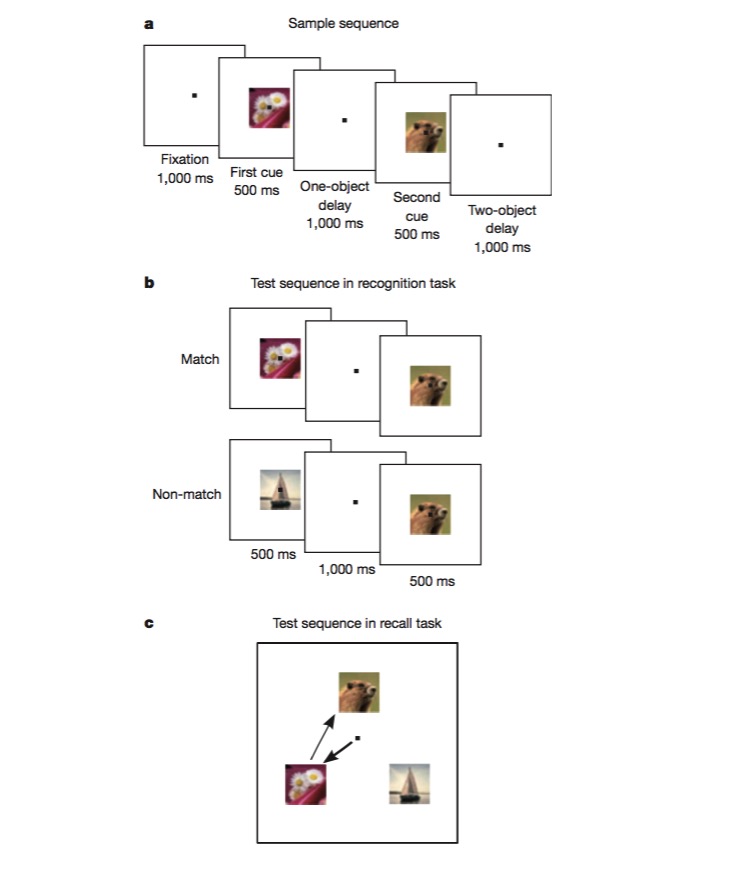
В этой задаче мыши сначала обучаются различать, является ли изображение идентичным предыдущему (признание), а затем обучаются судить о последовательности появления двух разных изображений (воспоминание). Для выполнения такой задачи мыши должны иметь возможность кодировать различные аспекты задачи, такие как тип задачи (воспоминание или признание), тип изображения и т. Д. Именно это является идеальным тестом на наличие смешанного нелинейного кодирования.

В этой статье мы узнали, что внедрение нелинейных элементов в дизайн нейронных сетей может значительно улучшить способность к распознаванию паттернов, и что SVM использует это для решения нелинейных классификационных задач.

Мы изучаем функцию мозга, обрабатывая данные методами машинного обучения, например, находя ключевые измерения проблемы с помощью ПЦА, а затем используя мысли, идентифицирующие модели машинного обучения, для понимания нейронного кодирования и расшифровки, и в конечном итоге, если мы получим новое вдохновение, мы сможем улучшить методы машинного обучения. Для мозга или алгоритма машинного обучения, в конечном итоге, самое важное - получить наиболее подходящий способ отображения информации, а с хорошей отображением все становится проще.

Снимок из фильма “Круизный корабль”