Лук-порей и спред спроса и предложения: предварительное исследование модели EKOP

• #### 1 Преамбула

В последнее время я была очень занята, и с момента последней статьи прошло уже несколько месяцев. За эти месяцы произошло многое, некоторые из которых были черными лебедями для моей собственной жизни. Но эти переживания показали мне, что жизнь, как и торговля, имеет свои взлеты и падения, полная неизвестности.

Мы все знаем, что активные акции обычно имеют небольшую разницу в цене покупки и продажи (spread), а неактивные акции - наоборот. Почему это происходит? Можно ли объяснить разницу в цене с помощью простой красивой математической модели?[В этой статье я расскажу об основах этой модели. Применение модели будет подвергнуто дальнейшему анализу в последующих статьях (если у меня будет время). Красота математической модели в том, что в этой статье показана ее простота.

• #### 2 Предположения о процессе сделки

Когда мы говорим о финансовой модели, самое важное - обратить внимание на предположения этой модели. Хорошие финансовые модели имеют свои собственные предположения: они не будут слишком сильными, чтобы не иметь универсальности; они не будут слишком слабыми, чтобы не получать красивых и простых результатов. Основные предположения модели EKOP следующие:

Гипотеза 1: мы говорим о сделках с акциями, торги совершаются в разрозненные дни, в течение суток. Гипотеза 2. То есть, сделки трейдеров происходят в 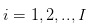в разрозненные торговые дни.

• Плохие новости: мы записываем стоимость акций как
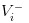
• Хорошие новости: мы записываем стоимость акций в
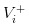
• Если нет новостей, мы запишем стоимость акций в

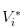
Очевидно, что у нас есть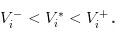

Гипотеза 2: В какой-то день

вероятность возникновения события, влияющего на цену акции, при 1-α вероятности не возникновения события, влияющего на цену акции. В те дни, когда происходит событие, также есть вероятность возникновения δ плохого события, которое приведет к снижению цены акции, а вероятность возникновения 1-δ хорошего события, которое приведет к повышению цены акции.

Предположение 3: участники торговли акциями являются маркетологами (market makers, MM), информированными трейдерами (informed traders, IT) и неинформированными трейдерами (uninformed traders, UT). Они следуют следующему поведению:

MM всегда готов к тому, чтобы купить или продать одну единицу, выполняя свои обязанности в качестве маркетолога. MM является нейтральным к риску, поэтому цена, на которую он размещает свою заявку, является справедливой, по его мнению.

ИТ торгует только в дни, когда происходят новости, их торговое поведение является пассивным процессом. В какой-то день, если происходят плохие новости, он выставляет проданную цену со скоростью прибытия в μ; а в дни, когда происходят хорошие новости, он выставляет покупательную цену со скоростью прибытия в μ.

UT, то есть наша бедная капуста, из-за преимущества отсутствия новостей, их торговая деятельность также является бесперебойным процессом, в течение каждого дня они вешают куплю и продажу на прибытии. Заметьте, что все процессы подзона здесь независимы друг от друга. Мы можем представить гипотезу 3 на графике, как следует.

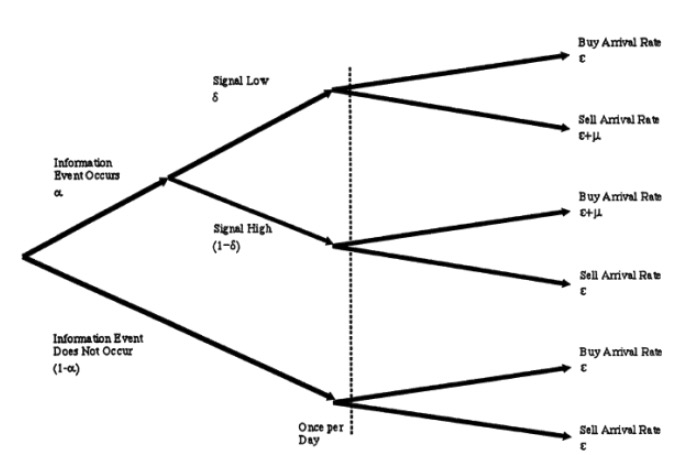
• #### 3 Обновление сделок и цен

Мы знаем, что рыночные торговцы, как правило, работают в крупных компаниях. Они очень умны, и в течение долгой борьбы с ИТ и ИТ они подвели итог всех модельных параметров в этой древообразной диаграмме с помощью большого количества исторических данных. Но, к счастью, они не настолько хороши, как осведомленные торговцы, и они не знают, как осведомленные торговцы, что произошло что-то важное в этот день.

Теперь давайте попробуем взять на себя роль MM, который борется с ИТ и ИТ. В какой-то момент времени t, мы записываем себя как вектор для предположений о вероятности того, что что-то произойдет - ничего, что-то хорошее, что-то плохое.

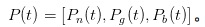。 Очевидно, что в начале дня, то есть в начале /upload/asset/7a5565722b92d2accf331f58923d6bab702659de.png, я не видел ни одного отчета, поэтому все, что я могу сделать, это предположить, что вероятность того, что ничего не произойдет, составляет α, вероятность того, что что что-то хорошее произойдет, составляет /upload/asset/c9cf50c6146a25c662c593ed229845822bfac7a5.png, а вероятность того, что что-то плохое произойдет, составляет /upload/asset/87418f07b12fce65f4c3f70b24e0d94e2e19f769a.png.

Как же обновить эту вероятность? Хорошо, мы, рыночные торговцы, знаем формулу Байеса. Когда мы наблюдаем, как приходит продажа, мы используем закон Байеса, чтобы обновить нашу собственную оценку вероятности.

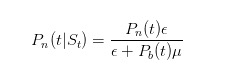
Молекула этого выражения говорит, что только неосведомленный трейдер будет продавать в случае отсутствия новостей; а делитель говорит, что в любой момент неосведомленный трейдер будет продавать в случае нет новостей, а осведомленный трейдер будет продавать в случае неудач в случае неудач. Аналогично, мы можем предположить, что

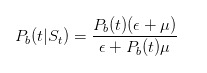
и

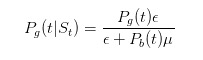
Перед тем как мы продолжим делать выводы, давайте сделаем несколько простых тестов. Мы сказали, что если мы увидим проданный билет, то мы должны увеличить нашу оценку вероятности того, что что-то плохое произойдет.

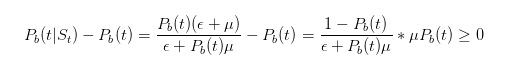
Это говорит о том, что наши выводы подтверждают нашу интуицию.

После того, как мы получим обновленную вероятность, мы сможем рассчитать справедливую цену, которая будет нашей рыночной ценой покупки, выраженной как

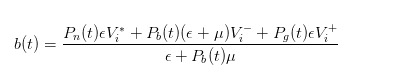
С помощью аналогичных выводов, мы можем увидеть, что, когда приходит покупатель, цена продажи, которую мы, как маркетологи, сообщаем, должна быть

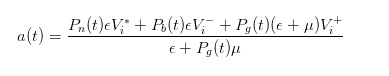
• #### 4 Выражение разницы в цене после изменения цены

Вышеуказанное выражение цены покупки и продажи недостаточно интуитивно, мы можем ввести ожидаемую стоимость акции в момент t для упрощения выражения.

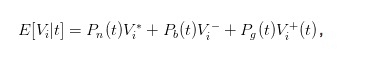
Таким образом, мы можем преобразовать выражения bid и ask в

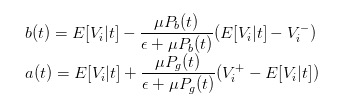
Таким образом, мы можем четко выразить разницу в цене как

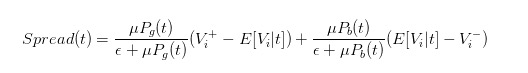
• #### 5 Влияние поведения трейдеров на разницу в ценах

Теперь, когда мы знаем, что такое разница в цене, мы можем проанализировать, как разные трейдеры влияют на разницу в цене.

Чем больше соломы, тем меньше разрыв. Обратите внимание, что ε - это доходность для неосведомленных торговцев (давайте назовем их соломы), и если есть ε >> μ, мы можем обнаружить, что / upload/asset/539e0cfb1aae368277dd0e3840448b6a39abd087.png оба элемента будут приближаться к нулю, что означает, что распространение также будет приближаться к нулю. Если мы перейдем к другой крайности, предположим, что на рынке нет салата, а есть только группа осведомленных трейдеров, то мы увидим, что цена, которую мы вывешиваем, будет 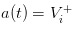и /upload/asset/1248ca7d3d472490982c9d0aa7b2e04b51269b18.png, поэтому осведомленные трейдеры обнаруживают, что они не могут получить прибыль от покупки и продажи, и рынок неизбежно замернет.

Посмотрите, мы можем сделать такие интересные и глубокие выводы, основываясь на некоторых предположениях, используя очень простые математические выводы, и это, наверное, огромная прелесть математических моделей.

[1] Easley, David, et al. “Liquidity, information, and infrequently traded stocks.” The Journal of Finance 51.4 (1996): 1405-1436.