Мысли о стратегиях высокочастотной торговли (1)
 3
3
 4856
4856

В статье рассматриваются стратегии высокочастотной торговли цифровыми валютами, включая источники прибыли (в основном за счет колебаний рынка и скидок на биржевые комиссии), вопросы размещения ордеров и управления позициями, а также метод моделирования объема торгов с использованием распределения Парето. Кроме того, для бэктестинга использовались данные о транзакциях и оптимальных ордерах, предоставленные Binance, а другие вопросы стратегий высокочастотной торговли планируется подробно обсудить в последующих статьях.
Ранее я написал две статьи о высокочастотной торговле цифровыми валютами. Подробное введение в высокочастотные стратегии для цифровых валют, Заработайте 80 раз за 5 дней, сила высокочастотной стратегии. Но это можно рассматривать только как обмен опытом и общие разговоры. На этот раз я планирую написать серию статей, чтобы представить идеи высокочастотной торговли с самого начала. Я надеюсь быть максимально кратким и понятным. Однако из-за моего ограниченного уровня и глубокого понимания высокочастотной торговля, эта статья — только отправная точка. Надеюсь, эксперты меня поправят.
Высокочастотные источники прибыли
Как упоминалось в предыдущих статьях, высокочастотные стратегии особенно подходят для рынков с чрезвычайно волатильными подъемами и падениями. Изучите изменение цен на товар за короткий период времени, которое состоит из общих тенденций и колебаний. Если мы сможем точно предсказать изменения в трендах, мы, безусловно, сможем заработать деньги, но это также и самое сложное. В этой статье в основном представлены стратегии высокочастотных мейкеров, и мы не будем затрагивать этот вопрос. На волатильном рынке, если стратегия размещения ордеров вверх и вниз выполняется достаточно часто, а размер прибыли достаточно велик, она может покрыть возможные убытки, вызванные тенденцией, так что вы можете получать прибыль, не прогнозируя рынок. В настоящее время все транзакции мейкеров на биржах получают скидки на транзакционные сборы, что также является компонентом прибыли. Чем интенсивнее конкуренция, тем выше должна быть доля скидок.
Проблема, которую необходимо решить
Стратегия размещает ордера на покупку и ордера на продажу одновременно. Первый вопрос — где размещать ордера. Чем ближе ордер к рынку, тем выше вероятность транзакции. Однако на нестабильном рынке мгновенная цена транзакции может быть далека от рыночной. Если ордер размещен слишком близко, вы не сможете получить достаточную прибыль. Вероятность исполнения ордеров, размещенных слишком далеко, низкая. Это проблема, которую необходимо оптимизировать.
Контролируйте свое положение. Чтобы контролировать риски, стратегия не может накапливать слишком много позиций в течение длительного времени. Эту проблему можно решить, контролируя расстояние между ордерами, объем ордера, общий лимит позиций и т. д.
Для достижения вышеуказанных целей необходимо смоделировать и оценить вероятность транзакции, прибыль от транзакции, оценку рынка и другие аспекты. Существует множество статей и документов в этой области, которые можно найти по ключевым словам, таким как High-Frequency Trading , Книга заказов и т.д. В Интернете есть много рекомендаций, но я не буду на них здесь останавливаться. Кроме того, лучше всего установить надежную и быструю систему бэктестинга. Хотя высокочастотные стратегии можно легко проверить с помощью реальной торговли, чтобы убедиться в их эффективности, бэктестинг все равно может предоставить больше идей и сократить стоимость проб и ошибок.
Требуемые данные
Binance предоставляет данные по каждой транзакции и лучшим ордерамскачатьГлубокие данные необходимо загружать с помощью API из белого списка, или вы можете собрать их самостоятельно. Для целей бэктестинга вы можете просто использовать собранные данные о транзакциях. В данной статье в качестве примера взяты данные HOOKUSDT-aggTrades-2023-01-27.
from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
Столбцы транзакций следующие:
- agg_trade_id: идентификатор агрегированного транзакционного ордера,
- Цена: цена сделки
- Количество: Количество транзакций
- first_trade_id: В коллекции может быть несколько транзакций одновременно, учитываются только одни данные, это идентификатор первой транзакции
- last_trade_id: идентификатор последней транзакции
- transact_time: время транзакции
- is_buyer_maker: направление транзакции, True означает, что ордер на покупку размещается мейкером, а ордер на продажу размещается тейкером
Видно, что в тот день было 660 000 транзакционных данных, и транзакции были очень активными. CSV-файл будет приложен в разделе комментариев.
trades = pd.read_csv('COMPUSDT-aggTrades-2023-07-02.csv')
trades
664475 rows × 7 columns
| agg_trade_id | price | quantity | first_trade_id | last_trade_id | transact_time | is_buyer_maker |
|---|---|---|---|---|---|---|
| 120719552 | 52.42 | 22.087 | 207862988 | 207862990 | 1688256004603 | False |
| 120719553 | 52.41 | 29.314 | 207862991 | 207863002 | 1688256004623 | True |
| 120719554 | 52.42 | 0.945 | 207863003 | 207863003 | 1688256004678 | False |
| 120719555 | 52.41 | 13.534 | 207863004 | 207863006 | 1688256004680 | True |
| … | … | … | … | … | … | … |
| 121384024 | 68.29 | 10.065 | 210364899 | 210364905 | 1688342399863 | False |
| 121384025 | 68.30 | 7.078 | 210364906 | 210364908 | 1688342399948 | False |
| 121384026 | 68.29 | 7.622 | 210364909 | 210364911 | 1688342399979 | True |
Моделирование объема отдельной транзакции
Сначала обработайте данные и разделите исходные сделки на группу активных транзакций ордеров на покупку и группу активных транзакций ордеров на продажу. Кроме того, исходные агрегированные данные транзакций представляют собой часть данных в одно и то же время, по одной и той же цене и в одном и том же направлении. Может быть активный заказ на покупку 100. Если он разделен на несколько транзакций с разными ценами, например как 60 и 40, будут сгенерированы два фрагмента данных, влияющих на оценку объема ордера на покупку. Поэтому необходимо выполнить повторное агрегирование на основе transact_time. После агрегации объем данных сократился на 140 000 записей.
trades['date'] = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index = trades['date']
buy_trades = trades[trades['is_buyer_maker']==False].copy()
sell_trades = trades[trades['is_buyer_maker']==True].copy()
buy_trades = buy_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
sell_trades = sell_trades.groupby('transact_time').agg({
'agg_trade_id': 'last',
'price': 'last',
'quantity': 'sum',
'first_trade_id': 'first',
'last_trade_id': 'last',
'is_buyer_maker': 'last',
'date': 'last',
'transact_time':'last'
})
buy_trades['interval']=buy_trades['transact_time'] - buy_trades['transact_time'].shift()
sell_trades['interval']=sell_trades['transact_time'] - sell_trades['transact_time'].shift()
print(trades.shape[0] - (buy_trades.shape[0]+sell_trades.shape[0]))
146181
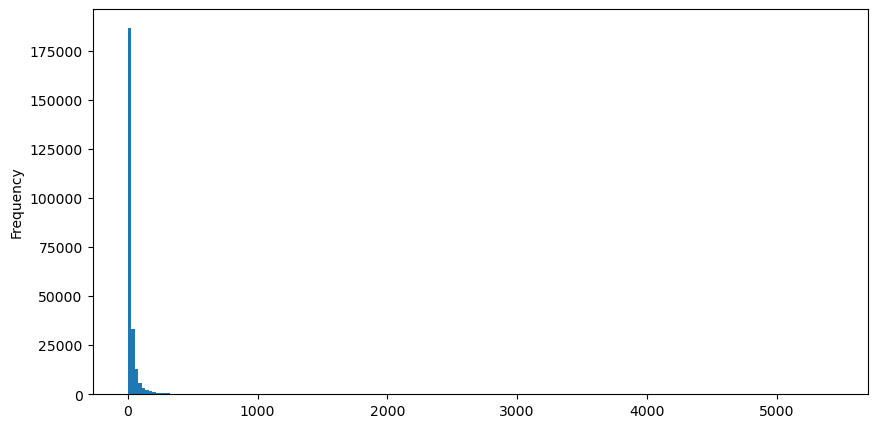
Взяв в качестве примера ордера на покупку, сначала нарисуйте гистограмму. Вы можете видеть, что эффект длинного хвоста очень очевиден. Большая часть данных сосредоточена в крайнем левом углу, но есть также небольшое количество крупных транзакций, распределенных в хвосте .
buy_trades['quantity'].plot.hist(bins=200,figsize=(10, 5));
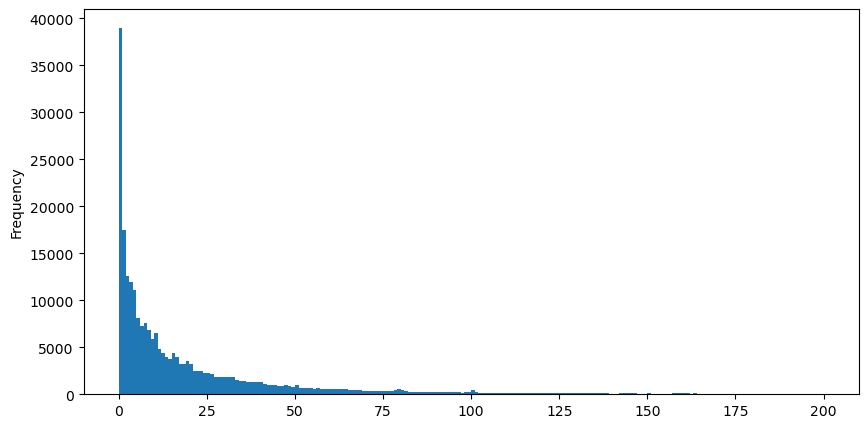
Для удобства наблюдения отсекаем хвост и наблюдаем. Видно, что чем больше объем торгов, тем ниже частота появления и тем быстрее тенденция к снижению.
buy_trades['quantity'][buy_trades['quantity']<200].plot.hist(bins=200,figsize=(10, 5));
Существует множество исследований распределения удовлетворенности объемом. Его степенное распределение также называется распределением Парето и является распространенной формой распределения вероятностей в статистической физике и социальных науках. В степенном законе распределения вероятность события определенного размера (или частоты) пропорциональна некоторому отрицательному показателю размера этого события. Главной особенностью этой формы распределения является то, что крупные события (т. е. далекие от среднего значения) происходят чаще, чем можно было бы ожидать во многих других распределениях. Это характеристика распределения объема торгов. Форма распределения Парето: P(x) = Cx^(-α). Ниже это будет продемонстрировано.
Рисунок ниже показывает вероятность того, что объем торговли больше определенного значения. Синяя линия — это фактическая вероятность, а оранжевая — смоделированная вероятность. Не беспокойтесь о конкретных параметрах здесь. Вы можете видеть, что это так удовлетворяют распределению Парето. Поскольку вероятность того, что объем заказа больше 0, равна 1, и для соответствия требованиям стандартизации уравнение распределения должно иметь следующий вид:
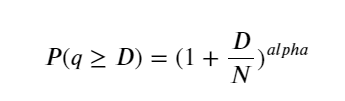
Где N — стандартизированный параметр. Здесь мы выбираем средний объем М и альфу -2,06. Конкретную оценку альфа можно рассчитать путем обратного вычисления значения P, когда D=N. В частности: альфа = log(P(d>M))/log(2) . Выбор разных точек приведет к немного разным значениям альфа.
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
alpha = np.log(np.mean(buy_trades['quantity'] > mean_quantity))/np.log(2)
mean_quantity = buy_trades['quantity'].mean()
probabilities_s = np.array([(1+depth/mean_quantity)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
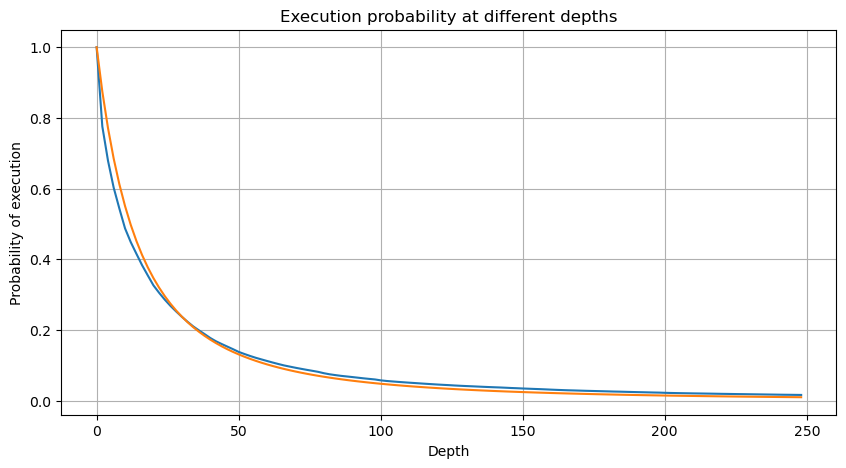
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
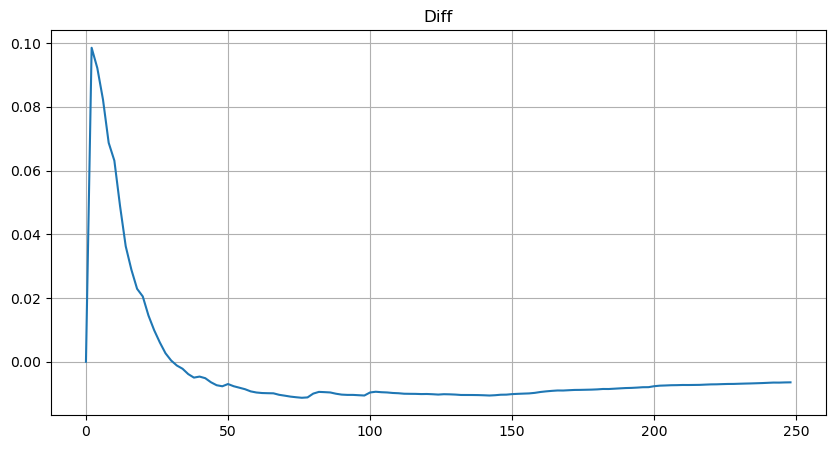
Но эта оценка только выглядит так. На рисунке выше мы отображаем разницу между смоделированным значением и фактическим значением. При небольшом объеме торгов отклонение велико, вплоть до 10%. Вероятность точки можно сделать более точной, выбирая разные точки при оценке параметров, но это не решает проблему отклонения. Это определяется разницей между степенным распределением и фактическим распределением. Для получения более точных результатов необходимо скорректировать уравнение степенного распределения. Я не буду вдаваться в подробности конкретного процесса, но меня осенило, и я понял, что на самом деле все должно быть следующим образом:
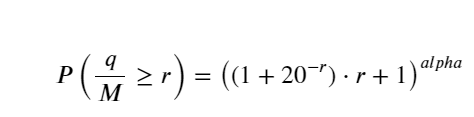
Для простоты здесь используется r = q/M для представления стандартизированного объема торговли. Параметры можно оценить таким же образом, как указано выше. На рисунке ниже показано, что максимальное отклонение после коррекции не превышает 2%. Теоретически коррекцию можно продолжать, но этой точности вполне достаточно.
depths = range(0, 250, 2)
probabilities = np.array([np.mean(buy_trades['quantity'] > depth) for depth in depths])
mean = buy_trades['quantity'].mean()
alpha = np.log(np.mean(buy_trades['quantity'] > mean))/np.log(2.05)
probabilities_s = np.array([(((1+20**(-depth/mean))*depth+mean)/mean)**alpha for depth in depths])
plt.figure(figsize=(10, 5))
plt.plot(depths, probabilities)
plt.plot(depths, probabilities_s)
plt.xlabel('Depth')
plt.ylabel('Probability of execution')
plt.title('Execution probability at different depths')
plt.grid(True)
plt.figure(figsize=(10, 5))
plt.grid(True)
plt.title('Diff')
plt.plot(depths, probabilities_s-probabilities);
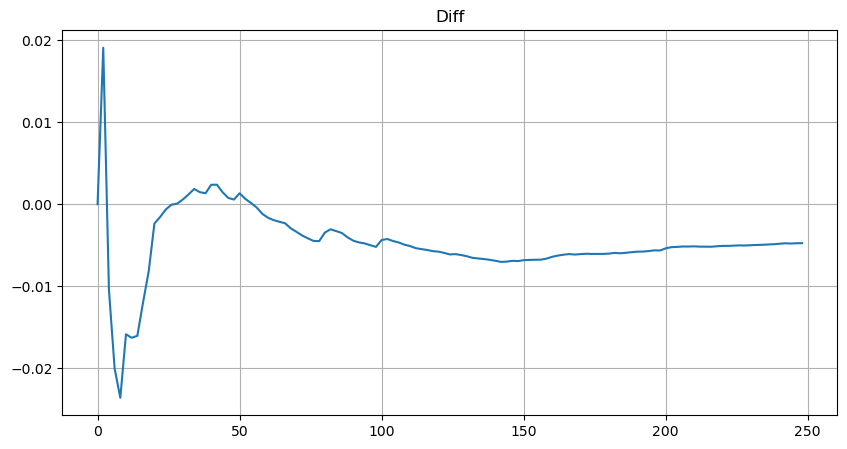
Принимая во внимание оценочное уравнение для распределения объема, следует отметить, что вероятность уравнения — это не истинная вероятность, а условная вероятность. На этом этапе мы можем ответить на вопрос: если произойдет следующий заказ, какова вероятность того, что этот заказ будет больше определенного значения? Другими словами, какова вероятность исполнения ордеров разной глубины (идеальная ситуация, не такая строгая, в теории в книге ордеров есть новые ордера и отмены, а также очереди на одной глубине).
Статья почти закончена, и есть еще много вопросов, на которые нужно ответить. Следующая серия статей попытается дать ответы.