В предыдущей статье был изучен интервал поступления заказов и показано, почему нам необходимо динамически корректировать параметры и как оценить качество оценки. В этой статье основное внимание будет уделено подробным данным и изучению средней цены (также называемой справедливой ценой, микроценой и т. д.).

Данные о глубине

Binance предоставляет возможность загрузки исторических данных о лучших котировках, включая best_bid_price: лучшую цену спроса, т. е. максимальную цену спроса, best_bid_qty: номер лучшей цены спроса, best_ask_price: лучшую цену спроса, best_ask_qty: номер лучшей цены спроса , transaction_time: временная метка. Эти данные не включают в себя отложенные ордера второго уровня и более глубокие. Анализируемая здесь рыночная ситуация относится к YGG на 7 августа. Колебания рынка в тот день были очень резкими, а объем данных достиг более 9 миллионов.

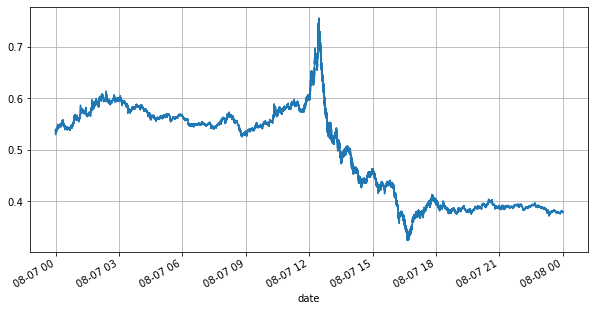
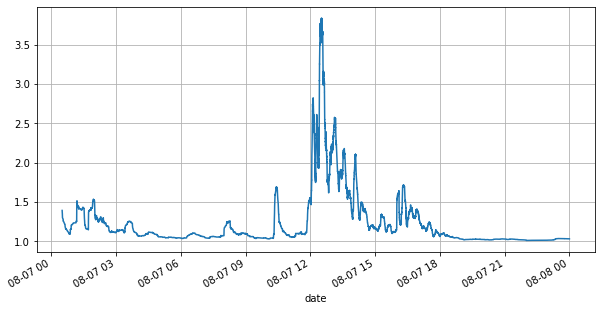
Сначала давайте посмотрим на рынок дня. Он имеет большие взлеты и падения. Кроме того, количество отложенных ордеров в день также сильно изменилось с колебаниями рынка. В частности, спред (разница между цена продажи и цена покупки) в значительной степени продемонстрировали колебательную ситуацию на рынке. Согласно статистике рынка YGG в тот день, в 20% случаев спред был больше 1 тика. В эту эпоху, когда на рынке конкурируют различные роботы, такая ситуация встречается редко.

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

books = pd.read_csv('YGGUSDT-bookTicker-2023-08-07.csv')

tick_size = 0.0001

books['date'] = pd.to_datetime(books['transaction_time'], unit='ms')
books.index = books['date']

books['spread'] = round(books['best_ask_price'] - books['best_bid_price'],4)

books['best_bid_price'][::10].plot(figsize=(10,5),grid=True);

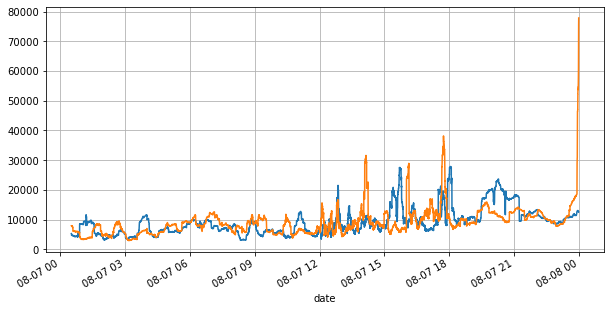
books['best_bid_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);
books['best_ask_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);

(books['spread'][::10]/tick_size).rolling(10000).mean().plot(figsize=(10,5),grid=True);

books['spread'].value_counts()[books['spread'].value_counts()>500]/books['spread'].value_counts().sum()

0.0001    0.799169
0.0002    0.102750
0.0003    0.042472
0.0004    0.022821
0.0005    0.012792
0.0006    0.007350
0.0007    0.004376
0.0008    0.002712
0.0009    0.001657
0.0010    0.001089
0.0011    0.000740
0.0012    0.000496
0.0013    0.000380
0.0014    0.000258
0.0015    0.000197
0.0016    0.000140
0.0017    0.000112
0.0018    0.000088
0.0019    0.000063
Name: spread, dtype: float64

Несбалансированные котировки

Из вышесказанного видно, что объемы заказов на покупку и продажу в большинстве случаев сильно различаются. Эта разница имеет сильный предсказательный эффект на краткосрочные рыночные условия. Причина аналогична причине, упомянутой в предыдущей статье: небольшие ордера на покупку часто приводят к снижению. Если отложенные ордера на одной стороне значительно меньше, чем на другой стороне, и если предположить, что объемы активных ордеров на покупку и продажу близки, то сторона с меньшими отложенными ордерами, скорее всего, будет поглощена, тем самым двигая цену. изменения. Несбалансированные котировки обозначены как I: 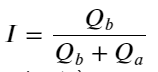Где Q_b представляет собой объем ордера на покупку (best_bid_qty), а Q_a представляет собой объем ордера на продажу (best_ask_qty).

Определить среднюю цену: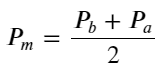

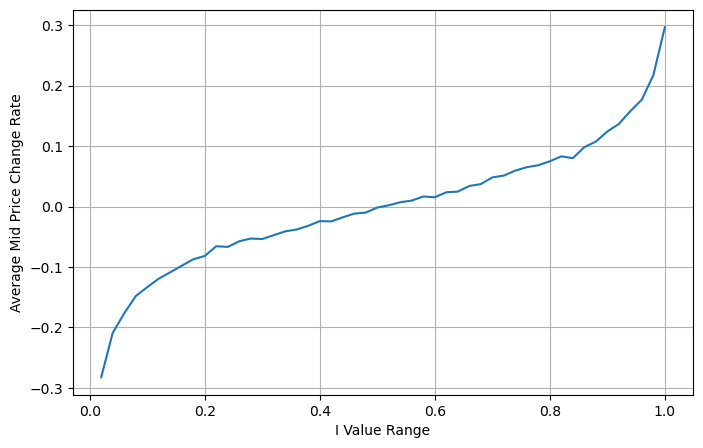
На следующем рисунке показана взаимосвязь между скоростью изменения средней цены в следующем интервале и дисбалансом I. Как и ожидалось, по мере увеличения I цена, скорее всего, вырастет, и чем ближе она к 1, тем больше величина дисбаланса. Изменение цен также ускоряется. В высокочастотной торговле целью введения средней цены является лучшее прогнозирование будущих изменений цен. Другими словами, чем меньше разница с будущей ценой, тем лучше определяется средняя цена. Очевидно, что дисбаланс отложенных ордеров дает дополнительную информацию для прогноза стратегии. Учитывая это, определяем средневзвешенную цену:

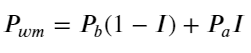
books['I'] = books['best_bid_qty'] / (books['best_bid_qty'] + books['best_ask_qty'])

books['mid_price'] = (books['best_ask_price'] + books['best_bid_price'])/2

bins = np.linspace(0, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['price_change'] = (books['mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Average Mid Price Change Rate');
plt.grid(True)

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['weighted_price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

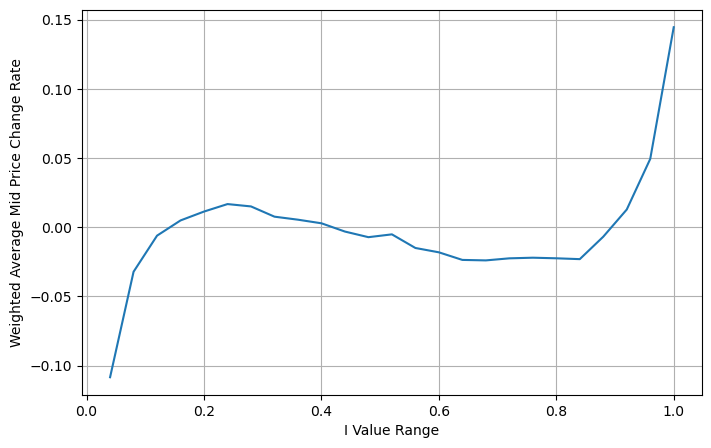
Скорректировать средневзвешенную цену

Из рисунка видно, что средневзвешенная цена изменяется гораздо меньше, чем разность I, а это значит, что средневзвешенная цена подходит лучше. Но все же есть некоторые закономерности, например, около 0,2 и 0,8, где отклонения относительно велики. Это показывает, что я все еще могу предоставить дополнительную информацию. Поскольку взвешенная средняя цена предполагает, что срок коррекции цены полностью линейный с I, это, очевидно, не так. Как видно из приведенного выше рисунка, когда I близко к 0 и 1, отклонение происходит быстрее и это не линейная зависимость.

Для более интуитивного взгляда I переопределено здесь:

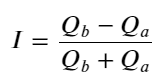
в это время:

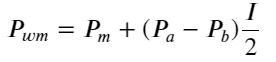
Наблюдая эту форму, мы можем обнаружить, что взвешенная средняя цена является поправкой к средней средней цене. Коэффициент поправочного члена — это Spread, а поправочный член является функцией I. Взвешенная средняя цена просто предполагает, что это отношение равно I/2. В это время проявляется преимущество скорректированного распределения I (-1,1). I симметрично относительно начала координат, что делает удобным для нас поиск подходящего соотношения функции. Обратите внимание на график, эта функция должна удовлетворять отношению нечетной степени I, что согласуется с быстрым ростом с обеих сторон и симметрией относительно начала координат. Кроме того, можно заметить, что значение вблизи начала координат близко к линейному, и когда I равно 0, результат функции равен 0, а когда I равно 1, результат функции равен 0,5. Итак, предположим, эта функция выглядит так:

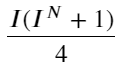
Здесь N — положительное четное число. После реальных испытаний лучше, когда N равно 8. На данный момент в данной статье предлагается пересмотренная средневзвешенная цена:

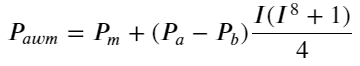
На данный момент изменение прогнозируемой средней цены по сути не имеет ничего общего с I. Хотя этот результат лучше, чем простая взвешенная средняя цена, его нельзя применять в реальной торговле. Это всего лишь идея, приведенная здесь. В статье С. Стойкова 2017 года был представлен метод цепей Маркова.Micro-Price, и дает соответствующий код, вы также можете его изучить.

books['I'] = (books['best_bid_qty'] - books['best_ask_qty']) / (books['best_bid_qty'] + books['best_ask_qty'])

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
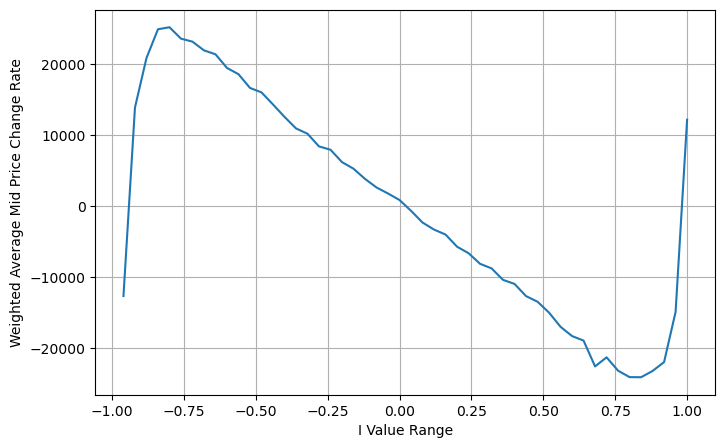
avg_change = books.groupby('I_bins')['weighted_price_change'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

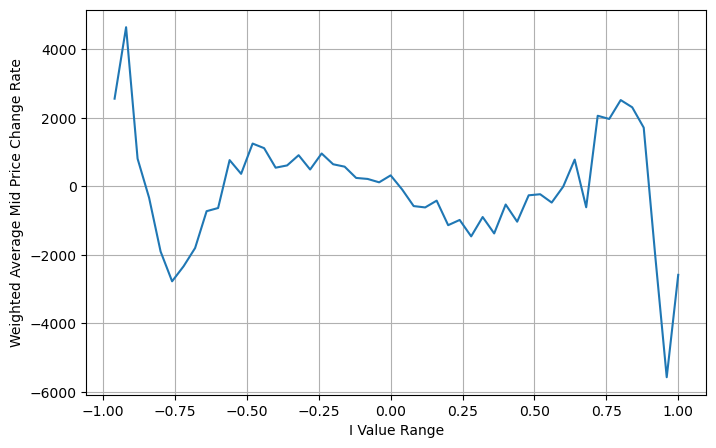
books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I'])*(books['I']**8+1)/4
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I']**3)/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

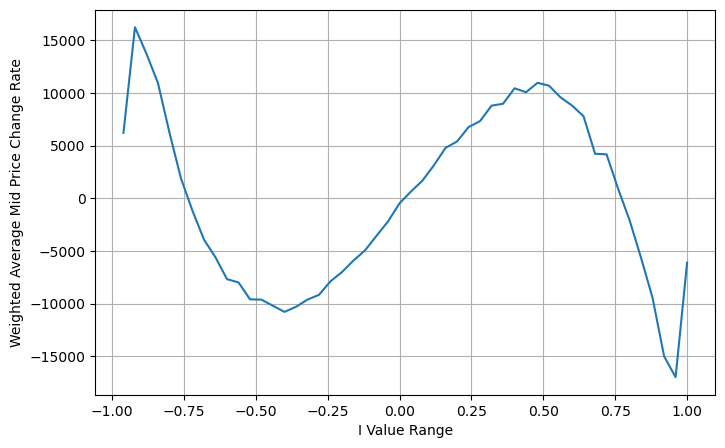
Подвести итог

Средняя цена очень важна для высокочастотных стратегий. Это прогноз будущих краткосрочных цен, поэтому средняя цена должна быть максимально точной. Все представленные выше средние цены основаны на рыночных данных, поскольку в анализе используется только одна рыночная цена. В реальной торговле стратегия должна максимально использовать все данные, особенно при наличии торговых обменов в реальной торговле, а прогноз средней цены должен быть проверен фактической ценой сделки. Я помню, что Стойков, кажется, опубликовал твит, в котором говорилось, что реальная средняя цена должна быть средневзвешенной вероятностью сделки «купи-продай». Этот вопрос как раз изучался в предыдущей статье. Из-за ограниченного объема эти вопросы будут подробно рассмотрены в следующей статье.