Стратегия прогнозирования временных рядов AR-GARCH
Почему традиционный технический анализ не работает на сложных рынках?
В области количественных сделок мы часто сталкиваемся с таким недоразумением: почему стратегии, основанные на простых движущихся средних или RSI, превосходно работают в некоторых рыночных условиях, а часто терпят неудачу в других? Ответ заключается в сложности финансовых временных рядов, которые не только связаны между собой, но и характеризуются волатильностью, изменяющейся с течением времени.
Эта стратегия, которую мы рассмотрим сегодня, искусно объединяет модель AR(2) с регрессией и модель GARCH(1,1) с условным дифференциалом, чтобы попытаться решить эту проблему с точки зрения статистики. Это не простое наложение технических показателей, а глубокое изучение основных особенностей финансовой временной серии.
AR2) Как модель улавливает эффект памяти цены?
В основе стратегии лежит применение модели саморегуляции AR[2]: что такое саморегуляция? Проще говоря, это использование прошлого себя для прогнозирования будущего себя[3].
r_t = φ₁ × r_{t-1} + φ₂ × r_{t-2} + ε_t
В коде уравнение Юле-Уокера решает коэффициенты φ1 и φ2:
c0 = calcAutoCovariance(returns, 0, lengthReg) // 滞后0期自协方差
c1 = calcAutoCovariance(returns, 1, lengthReg) // 滞后1期自协方差
c2 = calcAutoCovariance(returns, 2, lengthReg) // 滞后2期自协方差
phi1 = (c1 * c0 - c2 * c1) / denominator // 第一个自回归系数
phi2 = (c2 * c0 - c1 * c1) / denominator // 第二个自回归系数
Преимущество этого метода заключается в том, что он не полагается на субъективные суждения, а позволяет данным “говорить” сами за себя, обнаруживая закономерности, скрытые в ценовой последовательности.
Почему модель GARCH лучше отражает рыночные риски?
Одно только AR-модели недостаточно, поскольку волатильность финансовых рынков не является постоянной. Мы все знаем, что волатильность сосредотачивается, когда большие колебания часто сопровождаются большими колебаниями, а спокойные периоды обычно длятся дольше.
Модель GARCH ((1,1) была создана именно для этого:
σ²_t = ω + α × ε²_{t-1} + β × σ²_{t-1}
Это ясно видно из логики реализации в коде:
omega = (1 - adjustedAlpha - adjustedBeta) * longTermVar
garchVariance := omega + adjustedAlpha * math.pow(arResidual[1], 2) + adjustedBeta * garchVariance[1]
Ключевое понимание здесь заключается в том, что текущая условная сторона зависит не только от остаточного квадрата предыдущего периода ((короткосрочный удар), но и от условной сторон предыдущего периода ((долгосрочная устойчивость)). Параметр α контролирует влияние краткосрочного удара, β контролирует устойчивость колебаний.
Как логика торговли в стратегии может сбалансировать риск и выгоду?
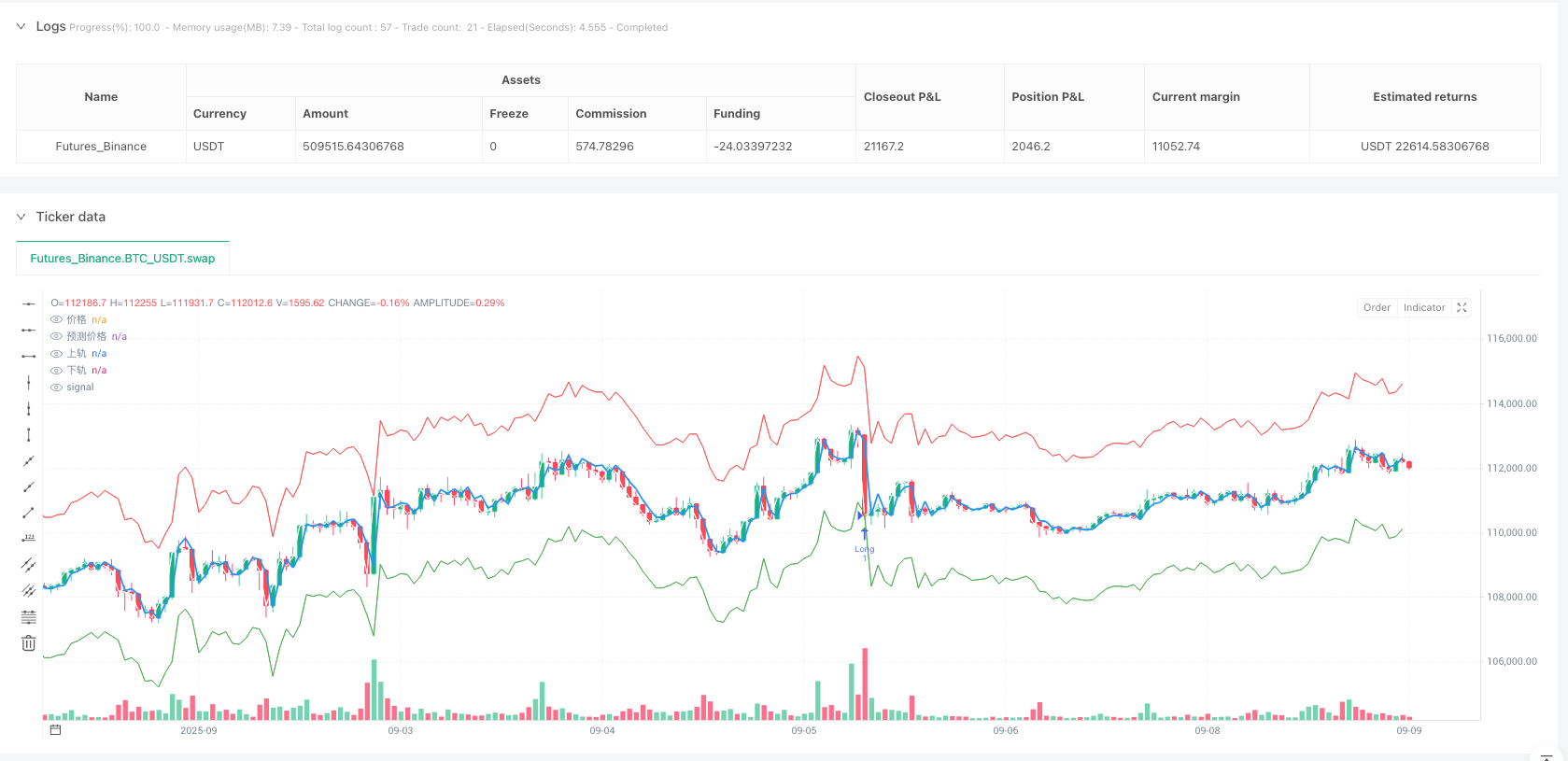
С помощью AR-прогнозов и оценки волатильности GARCH, стратегия создает динамические доверительные интервалы:
upperReturnBand = arReturnPredict + stdevFactor * garchStd
lowerReturnBand = arReturnPredict - stdevFactor * garchStd
Логика генерирования торговых сигналов отражает идею среднезначной регрессии:
- Если цена падает вниз по диапазону, то мы делаем больше.
- При повышении цены в верхнем диапазоне (shortSignal = rawPrice > upperPriceBand)
Хитрость этой конструкции заключается в том, что ширина доверительного диапазона динамически корректируется в зависимости от волатильности рынка. В периоды высокой волатильности диапазон становится шире, уменьшая частоту торговли; в периоды низкой волатильности диапазон сужается, увеличивая торговые возможности.
Какие ключевые вопросы требуют внимания в практическом применении?
1. Проверка стабильности модели В коде содержится важная проверка стабильности:
if stabilityCheck >= 0.99 or math.abs(phi2) >= 0.99
scaleFactor = 0.95 / math.max(stabilityCheck, math.abs(phi2) + 0.01)
Это обеспечивает стабильность AR-моделей и предотвращает рассеянные прогнозы.
2. Ограничение конвергентности параметров Модель GARCH требует, чтобы α + β < 1 гарантировало существование долгосрочной дифференциации:
if sumParam >= 0.999
scale = 0.99 / sumParam
3. Необходимость фильтрации Стратегия предоставляет опцию фильтрации RSI, что важно в практическом применении. Чисто статистические модели могут игнорировать тенденционные характеристики рынка, а добавление технических показателей может предоставить дополнительные подтверждающие сигналы.
Ограничения стратегии и пути улучшения
Несмотря на то, что эта стратегия в теории изящна, в практическом применении необходимо учитывать:
Выбор частоты данныхМодель AR-GARCH отличается значительным образом в различных периодах. Высокочастотные данные дают больше информации, но также вводят больше шума.
Временная изменчивость: В текущей реализации допускается, что параметры AR и GARCH постоянны в течение окна оценки, но реальная структура рынка может измениться.
Влияние на стоимость сделкиСтатистическая арбитражная стратегия обычно требует более высокой частоты сделок, а комиссионные и стоимость скольжения нельзя игнорировать.
В заключение: ценность статистического моделирования в количественных сделках
Стратегия AR-GARCH демонстрирует мощную силу современной статистики в финансовом моделировании. Это не просто совокупность технических показателей, а глубокое изучение статистических особенностей финансовых временных рядов.
Для квантовых трейдеров понимание таких стратегий имеет значение не только в их непосредственном применении, но и в развитии способности анализировать рынок с помощью статистического мышления. В современном мире искусственного интеллекта и машинного обучения эти классические статистические модели по-прежнему являются важным фундаментом для понимания рынка и построения стратегии.
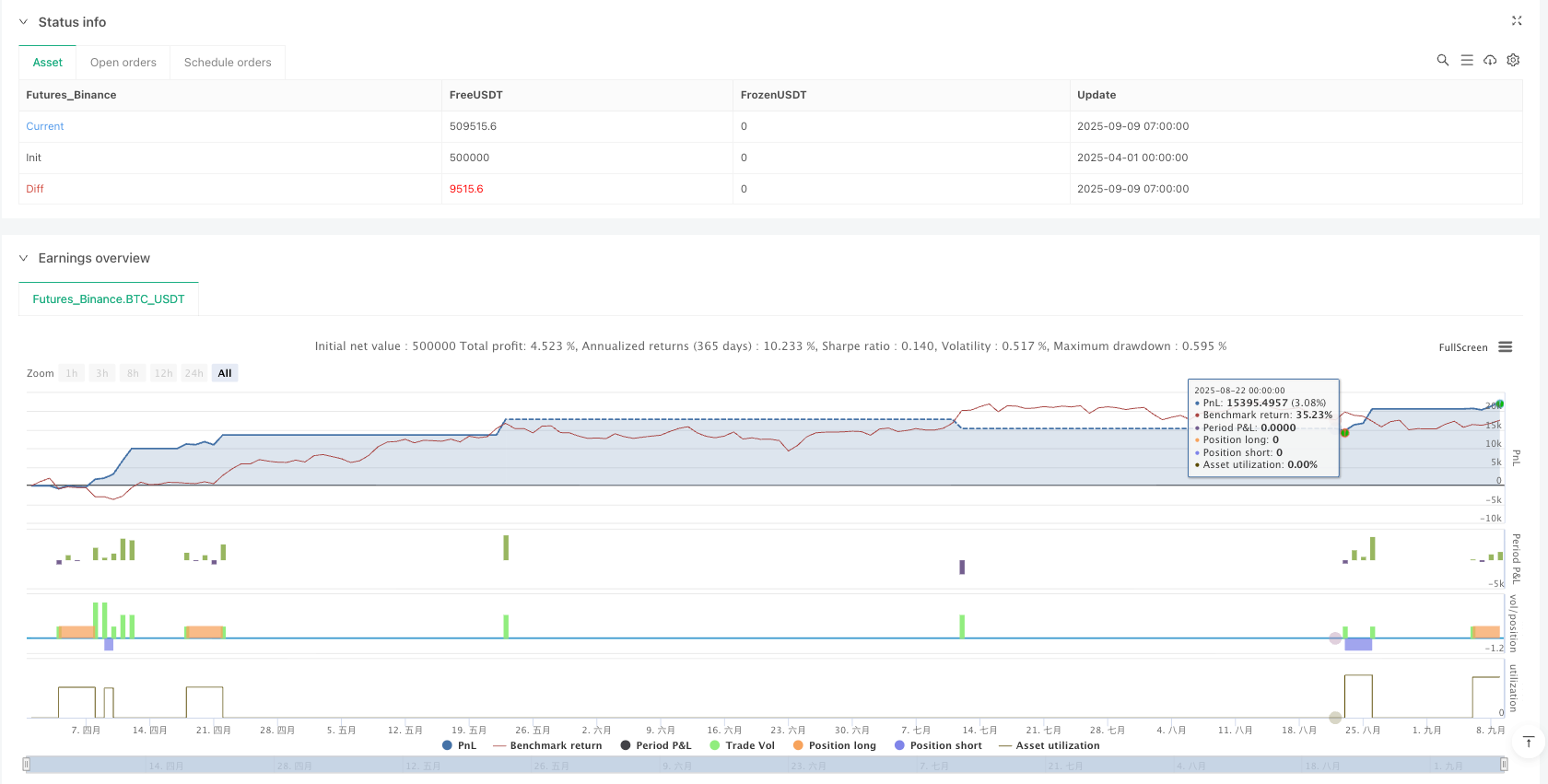
/*backtest
start: 2025-04-01 00:00:00
end: 2025-09-09 08:00:00
period: 1h
basePeriod: 1h
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT","balance":500000}]
*/
//@version=5
strategy("AR(2)-GARCH Strategy", overlay=true)
//策略参数设置:配置AR模型、GARCH模型和交易信号的各项参数
lengthReg = input.int(50, "AR估计窗口", minval=50, maxval=200);//AR模型回归窗口长度
//GARCH波动率模型参数:控制条件方差的计算
useGarch = input.bool(true, "启用GARCH波动率");//是否启用GARCH波动率建模
garchAlpha = input.float(0.1, "GARCH Alpha", minval=0.01, maxval=0.3, step=0.01);//GARCH模型alpha参数
garchBeta = input.float(0.85, "GARCH Beta", minval=0.5, maxval=0.95, step=0.01);//GARCH模型beta参数
//交易信号生成参数:控制买卖信号的敏感度
stdevFactor = input.float(2.0, "标准差倍数", minval=1.0, maxval=3.0, step=0.1);//交易波段的标准差倍数
//风险控制参数:设置止损止盈水平
stopLossPerc = input.float(2.0, "止损 (%)", minval=0.5, maxval=5.0, step=0.1);//止损百分比
takeProfitPerc = input.float(4.0, "止盈 (%)", minval=1.0, maxval=10.0, step=0.1);//止盈百分比
//RSI过滤器参数:添加技术指标过滤条件
useRsiFilter = input.bool(false, "启用RSI过滤");//是否启用RSI过滤器
rsiLen = input.int(14, "RSI周期", minval=7, maxval=21);//RSI指标计算周期
rsiOB = input.float(70, "RSI超买线", minval=60, maxval=80);//RSI超买阈值
rsiOS = input.float(30, "RSI超卖线", minval=20, maxval=40);//RSI超卖阈值
//数据预处理:计算收益率序列
rawPrice = close;//原始收盘价
returns = math.log(rawPrice / rawPrice[1]);//对数收益率序列
//获取滞后收益率数据:AR(2)模型需要前两期的收益率数据
returns1 = returns[1];//滞后1期的收益率
returns2 = returns[2];//滞后2期的收益率
//计算收益率序列的移动平均值:作为AR模型的均值项
returnsMean = ta.sma(returns, lengthReg);//收益率的简单移动平均
//AR(2)模型系数计算:使用Yule-Walker方程求解自回归系数
//自协方差函数计算:计算不同滞后期的自协方差
calcAutoCovariance(data, lag, length) =>
mean = ta.sma(data, length);//计算数据的均值
sum = 0.0;//协方差累计值
count = 0;//有效数据点计数
for i = lag to length - 1
if not na(data[i]) and not na(data[i-lag])
sum := sum + (data[i] - mean) * (data[i-lag] - mean);//计算协方差分子
count := count + 1;//累计有效数据点
count > 0 ? sum / count : 0.0;//返回协方差值
//计算AR(2)模型所需的自协方差:用于Yule-Walker方程
c0 = calcAutoCovariance(returns, 0, lengthReg);//滞后0期的自协方差(即方差)
c1 = calcAutoCovariance(returns, 1, lengthReg);//滞后1期的自协方差
c2 = calcAutoCovariance(returns, 2, lengthReg);//滞后2期的自协方差
//Yule-Walker方程求解:计算AR(2)模型的两个自回归系数
// φ₁ = (c₁c₀ - c₂c₁) / (c₀² - c₁²)
// φ₂ = (c₂c₀ - c₁²) / (c₀² - c₁²)
denominator = c0 * c0 - c1 * c1;//分母计算
phi1 = denominator != 0 ? (c1 * c0 - c2 * c1) / denominator : 0.0;//第一个自回归系数
phi2 = denominator != 0 ? (c2 * c0 - c1 * c1) / denominator : 0.0;//第二个自回归系数
//AR(2)稳定性检验:确保模型稳定性条件 |φ₁| + |φ₂| < 1 且 |φ₂| < 1
stabilityCheck = math.abs(phi1) + math.abs(phi2);//计算系数绝对值之和
if stabilityCheck >= 0.99 or math.abs(phi2) >= 0.99
scaleFactor = 0.95 / math.max(stabilityCheck, math.abs(phi2) + 0.01);//计算缩放因子
phi1 := phi1 * scaleFactor;//调整第一个系数
phi2 := phi2 * scaleFactor;//调整第二个系数
//AR(2)收益率预测:根据历史收益率和AR系数预测下一期收益率
arReturnPredict = returnsMean + phi1 * (returns1 - returnsMean) + phi2 * (returns2 - returnsMean);//AR(2)预测公式
//计算AR模型的预测残差:用于GARCH建模
arResidual = returns - arReturnPredict;//AR模型的预测残差
//GARCH(1,1)波动率建模:对AR残差进行条件方差建模
var float garchVariance = na;//GARCH方差变量
var float longTermVar = na;//长期方差变量
//长期方差初始化:使用历史残差计算初始方差值
if na(longTermVar) and bar_index > lengthReg
longTermVar := ta.variance(arResidual, lengthReg);//计算长期方差
//GARCH参数调整:确保参数满足收敛条件
adjustedAlpha = garchAlpha;//调整后的alpha参数
adjustedBeta = garchBeta;//调整后的beta参数
sumParam = garchAlpha + garchBeta;//参数和
if sumParam >= 0.999
scale = 0.99 / sumParam;//计算参数缩放比例
adjustedAlpha := garchAlpha * scale;//调整alpha参数
adjustedBeta := garchBeta * scale;//调整beta参数
//GARCH(1,1)递归更新:根据GARCH公式更新条件方差
if useGarch and not na(longTermVar) and not na(arResidual)
if na(garchVariance)
garchVariance := longTermVar;//初始化GARCH方差
else
omega = (1 - adjustedAlpha - adjustedBeta) * longTermVar;//GARCH常数项
garchVariance := omega + adjustedAlpha * math.pow(arResidual[1], 2) + adjustedBeta * garchVariance[1];//GARCH递归公式
//条件标准差计算:从条件方差计算标准差
garchStd = useGarch and not na(garchVariance) ? math.sqrt(math.max(garchVariance, 0.0001)) : ta.stdev(arResidual, 20);//启用GARCH时使用条件标准差,否则使用历史标准差
//收益率空间的置信区间构建:基于AR预测和GARCH波动率
upperReturnBand = arReturnPredict + stdevFactor * garchStd;//上轨:预测收益率加上标准差倍数
lowerReturnBand = arReturnPredict - stdevFactor * garchStd;//下轨:预测收益率减去标准差倍数
//将置信区间转换为价格空间:用于实际交易信号生成
//基于预测收益率计算预测价格
predictedPrice = rawPrice[1] * math.exp(arReturnPredict);//根据预测收益率计算预测价格
upperPriceBand = rawPrice[1] * math.exp(upperReturnBand);//上轨价格
lowerPriceBand = rawPrice[1] * math.exp(lowerReturnBand);//下轨价格
//交易信号生成:基于当前价格相对于置信区间的位置
longSignal = rawPrice < lowerPriceBand;//做多信号:当前价格低于下轨
shortSignal = rawPrice > upperPriceBand;//做空信号:当前价格高于上轨
//RSI过滤器:使用RSI指标过滤交易信号
if useRsiFilter
rsi = ta.rsi(rawPrice, rsiLen);//计算RSI指标
longSignal := longSignal and rsi < rsiOS;//做多信号需要RSI超卖确认
shortSignal := shortSignal and rsi > rsiOB;//做空信号需要RSI超买确认
//策略执行:根据交易信号开仓和平仓
//开仓操作:根据信号建立多头或空头仓位
if longSignal
strategy.entry("Long", strategy.long);//开多仓
if shortSignal
strategy.entry("Short", strategy.short);//开空仓
//风险控制:设置止损止盈条件
if strategy.position_size > 0
strategy.exit("Long Exit", "Long",
stop=strategy.position_avg_price * (1 - stopLossPerc/100),
limit=strategy.position_avg_price * (1 + takeProfitPerc/100));//多仓止损止盈
if strategy.position_size < 0
strategy.exit("Short Exit", "Short",
stop=strategy.position_avg_price * (1 + stopLossPerc/100),
limit=strategy.position_avg_price * (1 - takeProfitPerc/100));//空仓止损止盈
//图表显示:在图表上绘制价格、预测线和交易信号
//主要价格线和预测线:显示实际价格和基于收益率预测的价格
plot(rawPrice, color=color.white, linewidth=1, title="价格");//绘制实际价格线
plot(predictedPrice, color=color.blue, linewidth=2, title="预测价格");//绘制预测价格线
plot(upperPriceBand, color=color.red, linewidth=1, title="上轨");//绘制上轨线
plot(lowerPriceBand, color=color.green, linewidth=1, title="下轨");//绘制下轨线
//交易信号标记:在图表上标记买卖信号点
plotshape(longSignal, style=shape.triangleup, location=location.belowbar,
color=color.green, size=size.small, title="买入");//标记买入信号
plotshape(shortSignal, style=shape.triangledown, location=location.abovebar,
color=color.red, size=size.small, title="卖出");//标记卖出信号