ریاضی اور جوا

• ہم جانتے ہیں کہ جوئے بازی امکانات کا کھیل ہے ، اور یہ کچھ عجیب جوئے کے نتائج ہیں جو ریاضی دانوں پاسکل اور عظیم ریاضی دان فرماٹ کی دلچسپی کا باعث بنے ہیں ، جنہوں نے خط و کتابت کے ذریعے ، امکانات کے نظریہ کے کچھ اصول پیش کیے ، جس سے امکان کی بنیاد رکھی گئی ہے۔ آج کا شمارہ جوئے میں امکانات کے کچھ دلچسپ موضوعات کا تعارف پیش کرتا ہے ، تاکہ آپ کو معلوم ہو کہ جوئے بازی کے لئے ، آپ کو اچھی طرح سے سوچنے کی ضرورت ہے۔

• 1، کامل جوا

این بی اے کی ٹیم لیکوسٹ اور کوئلو ٹیم کا ایک میچ ہے ، دونوں ٹیموں کے وفادار پرستار ہیں ، انہیں کوئین کلب کلب اور کوئین کلب کلب کہیں۔ شائقین کو یقینی طور پر لگتا ہے کہ ان کی حمایت کرنے والی ٹیم جیتنے کا زیادہ امکان ہے ، لہذا وہ آپ سے شرط لگانا پسند کریں گے۔ فرض کریں کہ کوئین کلب کلب کا خیال ہے کہ لیکوسٹ جیتنے کا امکان p ہے ، کوئین کلب کلب کا خیال ہے کہ کوئین کلب جیتنے کا امکان q ، p اور q دونوں 50٪ سے زیادہ ہونا چاہئے۔

اس کا طریقہ کار یہ ہے کہ ہم اسی طرح کی شرط لگاتے ہیں جس طرح ہم نے فینسی اور گینس کے جوتے لگائے تھے۔ اگر ہم جیت جاتے ہیں تو ہمیں y ڈالر ملتے ہیں اور اگر ہم ہار جاتے ہیں تو ہم x ڈالر کھو دیتے ہیں۔ جب تک کہ y> x ہم جیت جاتے ہیں۔ اور x اور y کو صرف مندرجہ ذیل دو سادہ عدم مساوات کو پورا کرنے کی ضرورت ہے ، فینسی اور گینس کے جوتے کی متوقع آمدنی مثبت ہے ، ہم سے شرط لگائیں گے:

```
p * x - ( 1-p ) * y > 0
q * x - ( 1-q ) * y > 0
```

y>x کی پابندی کے ساتھ، جو تصویر تیار کی گئی ہے وہ تین سیدھی لائنوں سے گھرا ہوا علاقہ ہے، جس میں کسی بھی نقطہ کی کوآرڈینیٹ ویلیو ((x، y) ایک لازمی حل ہے۔ اگر p>q، تو حل مندرجہ ذیل گراف میں نیلے رنگ کا حصہ ہے:

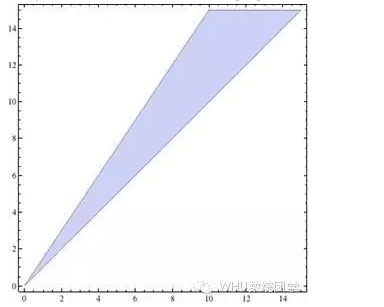
یہ سوال بالکل حل ہو گیا ہے، لیکن اس میں ایک اور سوال بھی ہے، جس کے بارے میں یقین ہے کہ قارئین جلد ہی اس کی مضحکہ خیز بات کو جان لیں گے: چاہے وہ فنگس یا گینگ کی نسل کے لوگ ہوں، ان کی آمدنی کی توقعات مثبت ہیں، یعنی، وہ طویل عرصے میں پیسہ کمائیں گے، اور ہم مستحکم اور منافع بخش ہیں، تو پھر اتنا پیسہ کہاں سے آتا ہے، اور یہ کیسے ممکن ہے کہ ہر کوئی پیسہ کمائے؟

• ### 2 اور 3 کارڈ کا دھوکہ

یہ ایک اور ہوشیار چال ہے، ہم نے پہلے تین کارڈ تیار کیے ہیں، پہلا کارڈ اس کے برعکس سیاہ ہے، دوسرا کارڈ اس کے برعکس سرخ ہے، تیسرا کارڈ ایک طرف سیاہ اور دوسری طرف سرخ ہے۔ پھر کارڈ کو ایک خانے میں ڈال کر ہلا دیا جائے، اور مخالف کھلاڑی کو ایک فلیٹ کھینچ کر میز پر رکھ دیا جائے۔ اس کے بعد اس کے مخالف رنگ اور اس کے مخالف رنگ کا رنگ اور اس کے مخالف رنگ کا رنگ ایک ہی ہے۔ یہ چال منصفانہ نظر آتی ہے، مثلاً اگر ایک سطح پر سیاہ کارڈ کھینچ لیا جائے، تو کارڈ نمبر 1 یا نمبر 3 نہیں ہوتا، مخالف رنگ کا رنگ سیاہ یا سرخ نہیں ہوتا، اور اس کا امکان تقریباً ¹⁄₂ ہوتا ہے۔

حقیقت یہ ہے کہ ہمارے جیتنے کا امکان ¹⁄₂ نہیں ہے، بلکہ ²⁄₃ ہے۔ اس کھیل میں سب سے زیادہ پریشان کن بات یہ ہے کہ کارڈوں کی دو رخا شکل ہے۔ کھلاڑیوں کو تین نہیں، بلکہ چھ کارڈ ملتے ہیں: تین سیاہ اور تین سرخ۔ ہم ان چھوں کو A، B، C، D، E، F کے نام سے نمبر دیتے ہیں۔

جب کھلاڑی سیاہ رخ پر جاتا ہے تو ، A ، C ، D ، وغیرہ کے تین ممکنہ حالات ہیں ، اور ان کے پیچھے بالترتیب D ، F ، A ہیں ، جس میں سیاہ رنگ کا ²⁄₃ حصہ ہے۔

اس مسئلے کو سب سے پہلے 1889 میں فرانسیسی ریاضی دان جوزف لوئس فرانسوا برٹرینڈ نے پیش کیا تھا۔ اس مسئلے کے نتیجے کی وجہ سے یہ غیر متوقع تھا اور اسے برٹرینڈ کے باکس پیراڈوکس کے نام سے جانا جاتا ہے۔ 1950 میں امریکی ریاضی دان وارن ویور نے مذکورہ بالا کارڈ کھیل کا تعارف کیا ، جسے مارٹن گارڈنر نے تین کارڈوں کی دھوکہ دہی کہا۔

• ### 3، اتنی غیر معمولی نیچری اے

کبھی کبھی ہم جوا کھیلنا شروع کرتے ہیں تو پانی چھوڑ دیتے ہیں، پہلے دوسروں کو تھوڑا سا پیسہ جیتنے دیتے ہیں، لمبی تار ڈال کر بڑی مچھلی پکڑتے ہیں، اور آخر میں ایک ایک جال ختم کر دیتے ہیں۔ ذیل میں ایک بہترین مثال ہے۔ چار لوگ بریج کارڈ کھیل رہے ہیں، میں نے پہلے کہا: آؤ ایک ڈنڈہ کھیلتے ہیں، میرے پاس اب ایک اے ہے، کیا آپ اندازہ لگا سکتے ہیں کہ میرے پاس مزید اے ہیں؟ اس صورت میں آپ کا ہارنا بہت ممکن ہے، اس وقت آپ اپنے دل میں چپکے سے ایک پھولوں کا اے مقرر کرتے ہیں، مثلاً بلیک چیچ اے، جب کسی دور کے بعد ایک بلیک چیچ اے پکڑا جاتا ہے، تو یہ موقع آتا ہے: آؤ ایک اور ڈنڈہ کھیلتے ہیں، اب میرے پاس بلیک چیچ اے ہے، کیا آپ اندازہ لگا سکتے ہیں کہ میرے پاس مزید اے نہیں ہیں؟

بہت سے لوگوں کا خیال ہے کہ دو مٹر میں کوئی فرق نہیں ہے۔ ایک مٹر کے ساتھ کوئی فرق نہیں پڑتا۔ لیکن ان کے درمیان فرق ناقابل یقین حد تک بڑا ہے۔ آئیے پہلے مٹر کے ہونے کے امکانات کا حساب لگائیں:

  没有A的情形：C（48，13）
  至少有1张A的情形：C（52，13）－C（48，13）
  恰好有1张A的情形：4＊C（48，12）
  至少有2张A的情形：C（52，13）－C（48，13）－4＊C（48，12）
  事件X为至少有两张A，事件Y为至少有一张A，那么条件概率为：

  P（X｜Y）＝P（XY）／P（Y）=(C（52，13）－C（48，13）－4＊C（48，12）)/(C（52，13）－C（48，13）)≈37%

اس وقت میں نے اپنے آپ کو ایک اور A، کھونے کے لئے زیادہ آسان ہے ۔ لیکن پہلی جھاڑو کے بعد، تمام شرط لگانے کی مرضی کو متحرک کیا گیا ہے، ایک بار جب دوسری جھاڑو نے اپنے کپڑے تبدیل نہیں کیا تھا، تو انہوں نے بہت زیادہ شرط لگائی، اور پھر میں نے مزید A نہیں کیا، اور ہم اس کے نیچے ہیں۔ ذیل میں ہم دیکھیں گے کہ دوسری جھاڑو کی امکانات بہت مختلف ہیں:

  有黑桃A的情形：C（51，12）
  没有其它A的情形：C（48，12）
  还有其它A的情形：C（51，12）－C（48，12）
  事件X为还有其它A，事件Y为有黑桃A，条件概率为：

  P（X｜Y）＝P（XY）／P（Y）＝（C（51，12）－C（48，12））／C（51，12）≈56%。

WHU شماریاتی گروپولوجی سے ماخوذ