گاس اور بلیک سوان

---

• ### سیاہ سوان

میرے پاس ایک عرفیت ہے جو کہ چکن نظریہ نگار چکن ہے، جو کہ شاید کتابیوں کے لئے بھی ایک طعنہ ہے، کیونکہ میں واقعی بہت بیوقوف ہوں، اور ایک اصول کا خلاصہ بہت سی چیزوں سے کرنا پسند کرتا ہوں۔ میں شماریات کا ماہر ہوں، اور ہر طرح کی چیزوں کی اوسط تلاش کرنا پسند کرتا ہوں، ان کے چکن کے اصل چکن کو پکڑنے کے لئے، اور ہر طرح کی چھوٹی چھوٹی تفصیلات کو نظر انداز کرنے کے لئے، سوچتا ہے کہ صرف چیزوں کے مجموعی رجحان کو پکڑنے کے لئے، میں اپنے دماغ میں چکن اصول چکن کو زندگی میں حقیقت میں بدل سکتا ہوں، لیکن حقیقت میں میں ایک لکڑی کا بیوقوف ہوں، اور یہاں تک کہ پکا ہوا چکن کو اڑاتا ہوں۔

میرے والد نے بہت سی کتابیں نہیں پڑھی ہیں، لیکن وہ ایک مشہور جرات مندانہ فاکس ہیں، جو اکثر حقیقی زندگی میں حیرت انگیز طور پر جیت جاتے ہیں۔ ان کا ایک جملہ جو وہ اکثر مجھ سے کہتے تھے وہ یہ تھا: جیت یا شکست تفصیلات میں ہے۔

اس نے مجھے ، ایک نظریاتی طور پر ، الجھن میں ڈال دیا ، کیونکہ تفصیلات میرے لئے ریڈیو میں شور کی طرح نظرانداز کرنے کے قابل ہیں۔ میرا عقیدہ مشہور گاؤس ڈسٹری بیوشن (نیچے ملاحظہ کریں) سے آیا ہے ، جو ہمیں بتاتا ہے کہ کامیابی اور ناکامی انفرادی تفصیلات پر نہیں ، بلکہ مجموعی خصوصیات پر منحصر ہے۔

لیکن حقیقت میں والد صاحب کی بات درست ثابت ہوئی۔

اور میں سوچ رہا تھا کہ اس دنیا میں کیا غلط ہے جس پر میں نے ہمیشہ فخر کیا ہے، جس میں خوبصورت گیس کی گھنٹی کی شکل اور نیوٹن کے ہم آہنگی کے قوانین ہیں۔ میں نے حیاتیات کا مطالعہ شروع کیا اور رینگنے والے جانوروں کی دنیا میں اس کا جواب پایا، کیونکہ ایک جانور، بلیک سوان۔

اس سے پہلے کہ کالا سوان نمودار ہو ، سوان کی جھیل میں موجود سوان برف کے رنگ کے تھے۔ آپ تصور کر سکتے ہیں کہ اس طرح کی آسمان کی نیلی جھیل پر لاکھوں سفید سوان اڑ رہے ہیں اور دور سے ایسا لگتا ہے جیسے کیلی مزارو میں برف ہے۔ اس لئے میں نے سوچا کہ یہ سفید سوان کی علامت ہے ، اور میں نے 100٪ امکان کی طرف بڑھتے ہوئے پیش گوئی کی کہ تمام سوان سفید ہیں۔ یہاں تک کہ ایک دن ایک خالص سیاہ سوان جھیل پر اڑ گیا ، گویا یہ کسی اور دنیا سے آیا تھا ، لیکن اس نے میرے سوان کے خوابوں کو توڑ دیا۔ اس کے بعد سے میں نے سمجھا کہ حیاتیات کی دنیا میں خاصیتیں اس کی اصل ہوتی ہیں ، اوسط نہیں۔ خاصیتیں ہمیشہ آپ کی توقع سے کہیں زیادہ امکانات کے ساتھ آتی ہیں ، اور اس سے پہلے کی تھیوری کو توڑ دیتی ہیں۔

کلاسیکی طبیعیات کی دنیا اوسط کی دنیا ہے، جہاں تفصیلات اور استثناء کو نظر انداز کیا جاسکتا ہے۔ لیکن ایک بار جب وہ حیاتیاتی طور پر غالب علاقوں میں داخل ہوتے ہیں تو وہ راج کرتے ہیں۔

گندگی اور افراتفری سے بھری حیاتیاتی دنیا میں جانے سے پہلے ، آئیے ہم گوسٹ قانون کے تحت چلنے والے چمکتے ہوئے دن کی روشنی کے رقص کو یاد کریں۔

• ### Gauss کی تقسیم اور بڑی تعداد تھیوری اوسط کی طاقت

ہم اکثر چیزوں کی مجموعی حالت کو اوسط سے بیان کرتے ہیں، جیسے چینی مرد کی اونچائی ایک میٹر 7 ہے، اور اعداد و شمار کرنے والے لوگوں کے لیے اوسط تقریباً ایک عقیدہ بن جاتا ہے، ہم اکثر اس عقیدے کے پیچھے بنیادی مفروضہ بھول چکے ہیں- جوس کی تقسیم، اور صرف اس صورت میں جب ہمارے اعداد و شمار کی چیزیں جوس کی تقسیم کی نمائندگی کرتی ہیں، اوسط واقعی چیزوں کی خصوصیات کی نمائندگی کر سکتی ہے۔

ضروری معلومات: جمع کرنا اوسط کے برابر ہے۔ اوسط کا حساب کتاب اعداد و شمار پر انحصار کرتا ہے جس میں اعداد و شمار کو تقسیم کیا جاتا ہے جس میں بہت سارے اعداد و شمار کو شامل کیا جاتا ہے۔ اوسط کے قریب نمونہ کے انحراف کی مقدار کو معیاری فرق سے ظاہر کیا جاتا ہے۔ کلاسیکی نظریہ ہمیں بتاتا ہے کہ نمونہ کی گنجائش جتنی زیادہ ہوگی ، اوسط اس گروپ کی نمائندگی کرے گی جس کا مطالعہ کیا جارہا ہے۔

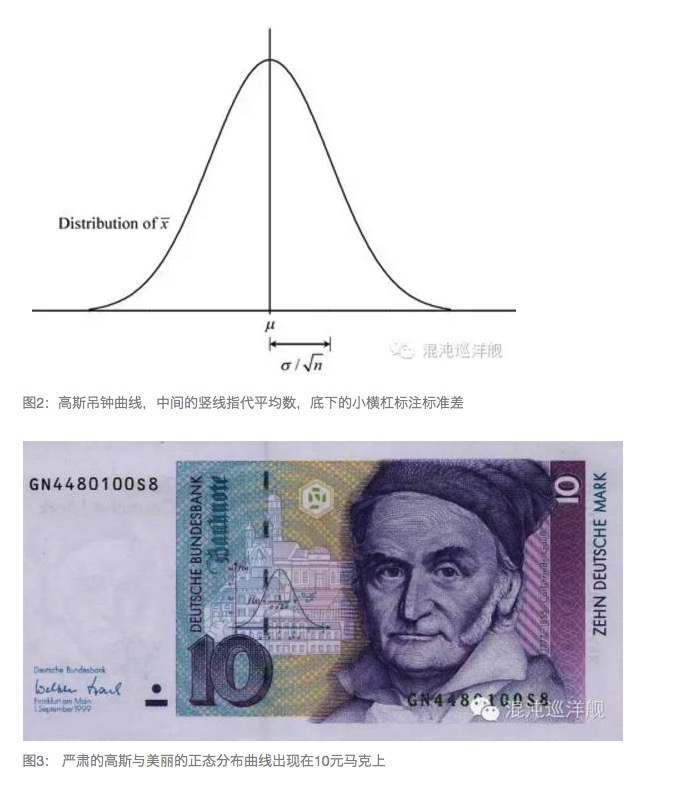
Gauss نے ہمیں جمع کی طاقت بتائی۔ ایک بے ترتیب واقعہ کے لئے، جیسے کہ جوئے بازی کے اڈوں میں جوتے، ہر بار ایک سے چھ تک کے نتائج کی مکمل طور پر پیشن گوئی نہیں کی جاسکتی ہے، لیکن اگر آپ دس ہزار بار شرط لگاتے ہیں، اور آپ ہر بار جو پوائنٹس حاصل کرتے ہیں وہ جمع کرتے ہیں تو آپ کو ایک ایسا نمبر ملتا ہے جو زیادہ سے زیادہ درست طریقے سے پیش گوئی کی جاسکتی ہے۔ اس نتیجے کو Gauss کی منحنی خطوط کے نام سے جانا جاتا ہے، جس میں دو خصوصیات ہیں، اوسط اور معیاری فرق۔ اوسط مجموعی رجحان کی وضاحت کرتا ہے اور معیاری فرق آپ کو غیر یقینی صورتحال کی مقدار بتاتا ہے۔ Gauss نے ہمیں بتایا کہ جیسے جیسے اضافہ ہوتا ہے ، معیاری فرق اوسط کے سامنے زیادہ سے زیادہ معمولی ہوتا جاتا ہے ، یہاں تک کہ اس کو نظرانداز کیا جاسکتا ہے ، یا اس کا کہنا ہے کہ بے ترتیب جمع کرنے کے ذریعے ، ایک بے ترتیب واقعہ ایک مقررہ واقعہ بن جاتا ہے ، اور ہمیں زیادہ سے زیادہ درست اوسط ملتا ہے۔ یہ قانون بڑی تعداد کا قانون کہا جاتا ہے۔

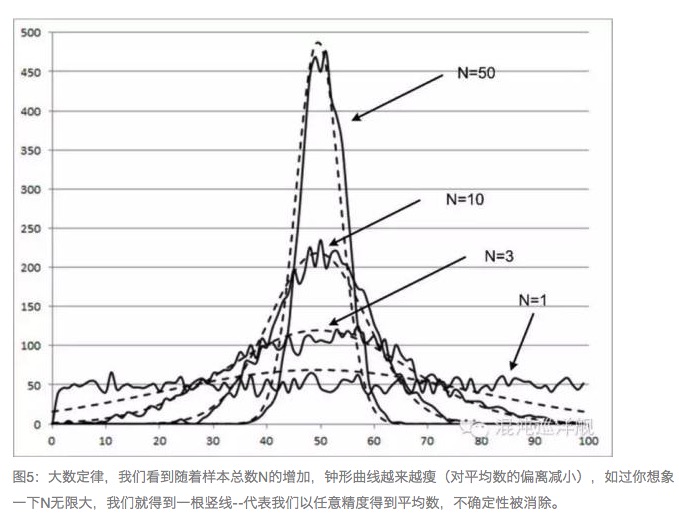
اکثریت کے قانون کی طاقت اس میں ہے کہ اس نے ایک یقینی دنیا کو بہت بڑی غیر یقینی صورتحال پر پیدا کرنے کی اجازت دی ہے۔ جیسے کل سورج طلوع ہوتا ہے تو موسم بہار میں پھول کھلیں گے ، ہم جانتے ہیں کہ ایسا نہ ہونے کا امکان تقریبا 0 ہے۔ دراصل ، یہ گاؤس کی تقسیم اور اکثریت کے نظریہ کی ضمانت ہے ، کیونکہ سورج طلوع ہونے کا پھول سورج اور پھولوں کے بے شمار ایٹموں اور انوولوں کے مشترکہ عمل کا نتیجہ ہے۔ جب ایک بار گڑھے پر بے شمار گڑھے مشترکہ طور پر کام کرتے ہیں تو ، اکثریت کا نظریہ اس بات کی ضمانت دیتا ہے کہ کسی بھی اعلی صحت سے متعلق چیز کا ہونا یقینی ہے۔ جیسے آپ کے پاس بے شمار فوجیوں کا ایک گروپ ہے ، آپ اب بھی تعداد پر بھروسہ کرکے جنگ جیت سکتے ہیں۔

عام تقسیم اور بڑی تعداد کے نظریات تمام یقین کی جڑ ہیں، کیونکہ ہماری نظر آنے والی دنیا بے شمار غیر یقینی مائیکرو عوامل کے مسلسل جمع کا نتیجہ ہے۔

تفصیلات کی اہمیت کے بارے میں انکشافات: وہ ہمیں بتاتے ہیں کہ جب فیصلہ کن واقعات کے لئے کافی عوامل موجود ہیں ، اور ہر چیز کے لئے کافی تعداد میں تجربات کیے جاتے ہیں ، تو چھوٹی چھوٹی تفصیلات کی کوئی اہمیت نہیں رہتی ہے ، کیونکہ وہ بہت زیادہ اضافے میں اوسط ہوجاتی ہیں۔

لیکن بہت جلد خوش نہ ہوں۔

• ### گوسٹ قانون کے پیچھے کی چالیں

A. تفصیلات کے عوامل آزاد ہیں

یہ تھوڑا سا تجریدی لگتا ہے، لیکن اصل میں یہ ہے کہ جو کچھ جمع ہے - جو چیزیں بناتی ہیں وہ ایک دوسرے کے ساتھ خفیہ طور پر بات چیت نہیں کر سکتی ہیں، جیسے کہ اگر آپ جانتے ہیں کہ تمام خواتین خفیہ طور پر آپ کے بارے میں اچھی یا بری بات کر رہی ہیں، تو آپ کو ملنے والے زیادہ سے زیادہ لوگوں کو آپ کے مثالی اوسط سے طے شدہ نتائج نہیں ملیں گے۔ کیونکہ تمام خواتین کو آپ کے ساتھ ملنے والے افراد کے بارے میں ایک ہی خیال ملتا ہے. آپ کو صرف ایک بڑے پیمانے پر معیاری فرق ملتا ہے، آپ کی پہلی ملاقات کی بے ترتیب زندگی کے نتائج میں بڑھا دیا جاتا ہے. ابتدائی اثرات کو بڑھا دیا جاتا ہے، ایمیزون کے جنگل کے نام نہاد تیتلی پنکھوں، اٹلانٹک پر ایک طوفان پیدا ہوتا ہے.

B. وقت کا فلیٹ شکل نہیں بدلتا

یہ ایک چھوٹی سی بات ہے۔ ایک سادہ سی مثال کے طور پر، اگر آپ پھینکتے ہیں تو آپ کے پاس ایک چھوٹا سا ٹکڑا ہوتا ہے، جس کے ساتھ آپ کے پاس ایک چھوٹا سا ٹکڑا ہوتا ہے، جس کے ساتھ آپ کے پاس ایک چھوٹا سا ٹکڑا ہوتا ہے، جس کے ساتھ آپ کے پاس ایک چھوٹا سا ٹکڑا ہوتا ہے، اور اس کے بعد آپ کو کبھی بھی ایک مستحکم اوسط نہیں ملتا ہے، لیکن آپ کو ایک گوسٹین اصول کے ساتھ جمع کرنا ہے، امید ہے کہ آپ اس رقم کو جیت لیں گے جو آپ کو اوسط سے ملتا ہے، آپ کو دھوکہ دیا گیا ہے.

بڑے پیمانے پر نظریہ ہماری بے ترتیب دنیا کی شناخت کی بنیاد ہے ، وہ ہمیں بتاتا ہے کہ کس طرح یقینی طور پر اتفاق کی بنیاد پر ابھرتا ہے۔ لیکن وہ نیوٹن کے پہلے قانون اور مثالی گیس ماڈل کی طرح ، ہموار سطحوں اور غیر باہمی تعامل والے بنیادی ذرات کی طرح حقیقی حیاتیات کی دنیا میں اس طرح کے خیالی طور پر موجود نہیں ہے ، حالانکہ ہمارے پاس کچھ قریب قریب حالات موجود ہیں۔

• ### بلیک سوان اثر اور طنزیہ تقسیم

گاسک منحنی خطوط اور بڑے پیمانے پر قوانین نے نظریاتی طبیعیات کی شاندار دنیا کو برقرار رکھا ، جہاں اچھی طرح سے سیکھنے سے دن بہ دن ترقی ہوتی ہے ، سیڈی لڑکی یقینی طور پر شہزادے سے ملتی ہے۔ تاہم ، بلیک سوان نے کہانیوں کو تباہ کردیا ہے۔

سیاہ سوان کی نوعیت یہ ہے کہ انفرادی مجموعی طور پر ، تفصیلات مجموعی طور پر فیصلہ کن اثرات مرتب کرتی ہیں۔ جب ایک سیاہ سوان پانی کی سطح پر آتا ہے تو ، سوان کی پوری جماعت کی خصوصیات بدل جاتی ہیں ، جب ایک خالص سفید ورلڈ سوان ہوتا ہے تو وہ مڈ گرے ہوجاتا ہے۔

Gaussian orthodoxy کے نقطہ نظر سے ، سیاہ سوان کے ظہور کا امکان نظرانداز کیا جاسکتا ہے ، کیونکہ ہم نے پہلے ہی دن کی روشنی میں بڑے پیمانے پر نمونوں کا حساب کتاب کیا تھا ، لیکن پھر بھی سیاہ سوان ظاہر ہوا ، اور اس کا ظہور غیر متوقع طور پر اتفاق سے ہوا ، کیا یہ ہماری خاص طور پر بدقسمتی ہے؟ غلط۔ لیکن غلط آپ نہیں ہیں ، یہ نارمل ڈسٹری بیوشن ہے۔

حیاتیات کی دنیا میں، غالب ہے طوطے کی تقسیم-power law، دراصل یہ بھی power کے انگریزی اصل معنی کی طرح، حقوق اور دولت سے متعلق ہے (دیکھیں شکل 6، پارلیٹو کی تقسیم) ۔ طوطے کی تقسیم کی ریاضی کا اظہار بہت سادہ ہے، مختلف طوطے کی تقسیم صرف طوطے کے اشاریہ کے فرق پر ظاہر ہوتی ہے۔ یہ گاسس کی تقسیم سے بنیادی طور پر مختلف ہے کہ، طوطے کی باقاعدہ تقسیم کے تحت ان واقعات کا امکان چھوٹا ہے جو نظرانداز کیا جا سکتا ہے، لیکن طوطے کی تقسیم کے تحت اتنے غیر معمولی نہیں ہیں۔ طوطے کے قانون کے نقطہ نظر سے، سیاہ سوان کی موجودگی قابل فہم ہے۔

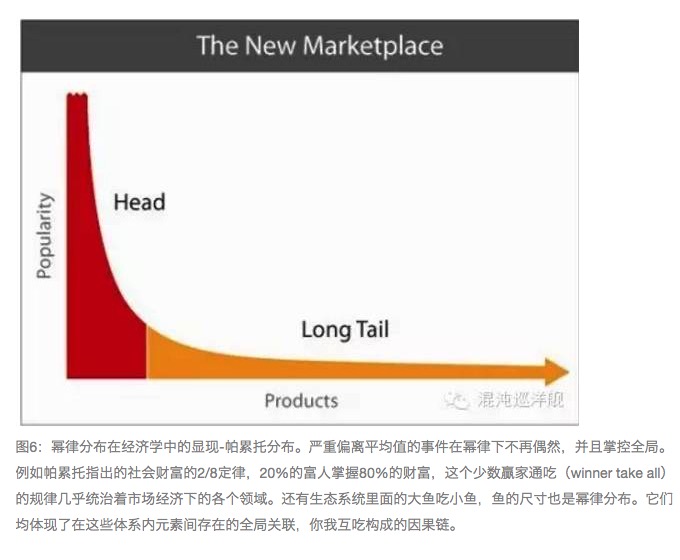
اس کے اثرات اتنے بڑے کیوں ہوتے ہیں؟ - یہاں جدید طبیعیات کے مرحلے کے نظریے نے اس کا حیران کن جواب دیا ہے۔ میں اس کی ایک خاص مثال پیش کرتا ہوں - برفانی تودہ۔ برفانی تودہ ایک پہاڑ کی چوٹی کے بڑے علاقے میں برفانی تودہ گرنا ہے ، جو کہ برفانی تودہ کی طرف جانے کے لئے تقریبا impossible ناممکن ہے۔ برفانی تودہ کلاسیکی سیاہ تودے کے واقعات کی تعریف پر پورا اترتا ہے ، جو عام طور پر تقریبا never کبھی نہیں ہوتا ہے ، اور اگر یہ ہوتا ہے تو ، یہ مہلک ہے۔

انتہائی حالت ایک نازک توازن کی حالت ہے ، جس میں برف کے ٹکڑوں کو ایک ساتھ رکھنے کی طاقت اور برف کے ٹکڑوں کو تحلیل کرنے کی طاقت تقریبا equal مساوی ہے ، لیکن جب تک کہ اس کی سطح تھوڑا سا جھکا ہوا ہو تب تک یہ تباہ کن ہے۔ آپ بڑے پیمانے پر برف کے ڈھلوان پر ایک چھوٹا سا پتھر پھینک دیتے ہیں ، اس پتھر کی کارروائی کا اثر مقامی برف کے ٹکڑوں میں جذب نہیں ہوتا ہے بلکہ پورے برف کے ٹکڑے میں پھیل جاتا ہے ، جیسے اونٹ کو کچلنے والے آخری گھاس کی طرح ، جس سے مجموعی طور پر توازن ختم ہوجاتا ہے۔

اس کے علاوہ ، یہ بھی کہا گیا ہے کہ اس کے بعد سے ، بلیک سوان نے اس کے خلاف جنگ لڑی ہے۔

برفانی تودے کی تھیوری کا مرکز اہم حالت میں تفصیلات کے کردار کی لامحدود توسیع ہے (مثبت آراء) ۔ ایک چھوٹا سا عنصر جو صرف مقامی طور پر محدود ہوتا ہے وہ اہم حالت میں پورے جسم میں پھیل جاتا ہے۔ برفانی تودے کی تھیوری ہر طرح کے شعبوں میں پھیل جاتی ہے ، جیسے زلزلے ، اسٹاک مارکیٹ میں تباہی ، مالی بحران ، اور یہاں تک کہ معاشرتی انقلاب کا آغاز۔

مساوی دشمنی کے دوران ، کسی بھی چھوٹی سی کردار کو بڑھاوا دیا جاسکتا ہے اور اس سے جنگ کا رخ موڑ سکتا ہے۔ مثال کے طور پر ، دونوں فریقوں کی طاقت برابر ہونے والی ایک لڑائی میں ، کسی ٹیم کے ایک ممبر کا موبائل فون بجتا ہے ، اس نے گھبراہٹ سے اپنا منہ کھولا ، اور اس کے نتیجے میں پوری ٹیم میں گھبراہٹ پھیل گئی ، جس کے نتیجے میں ایک موبائل فون کی گھنٹی بجنے سے ایک میچ تباہ ہوگیا۔ کہا جاتا ہے کہ ایک کیل کھو گئی ، ایک لوہا ٹوٹ گیا ، ایک لوہا ٹوٹ گیا ، ایک جنگی گھوڑا ٹوٹ گیا ، ایک جنگی گھوڑا ٹوٹ گیا ، ایک سوار زخمی ہوگیا ، ایک سوار زخمی ہوگیا ، ایک لڑائی ہار گئی ، ایک لڑائی ہار گئی ، ایک سلطنت ہلاک ہوگئی۔ اگر ایک گروہ جنگی گھوڑے ایک اہم جنگ میں ٹوٹ جاتے ہیں اور دونوں فورسز کو فتح کرنا مشکل ہے تو ، ایک سلطنت تباہ ہوجائے گی۔

زندگی کے سیلاب کی نوعیت ایک خاص تبدیلی ہے۔ اس لیے حیاتیات سے متعلق چیزیں، بشمول حیاتیات کی تاریخ اور ہماری انسانی تاریخ اور ہم میں سے ہر ایک کی زندگی، ایک اہم حالت میں ہوتی ہیں، وہ حالت جس میں بڑے بڑے اور چھوٹے چھوٹے برفانی تودے بھرے ہوتے ہیں، وہ غیر متوقع تفصیل جو مجموعی حالت کا تعین کرتی ہے۔ چونکہ آپ کل زندہ ہوں گے، تو سیاہ سوان اُڑ جائے گا۔ اصل میں، زندگی کی پیدائش، ارتقاء، ہماری پیدائش تک، ایک سلسلہ سیاہ سوان اُڑنے کا نتیجہ ہے، ہم خود ہی سیاہ سوان ہیں، پھر کیوں خوفزدہ ہوں کہ کل یہ پھر سے آپ کی سامنے والی کھڑکی پر سے گزر جائے گا۔

نوٹ: حیاتیاتی ارتقاء سب سے زیادہ اصلی نوعیت کا بلیک سوان اثر ہے ، جس میں حیاتیات کی تغیرات پہلے سے ہی استثنا ہیں ، اور جو تغیرات زندہ رہ سکتے ہیں وہ اس سے بھی زیادہ استثنا ہیں ، اور یہ وہی ہے جو اس طرح کے استثناؤں کی بجائے مرکزی دھارے میں ہے (اوسط) جس نے حیاتیات کے ارتقاء پر حکمرانی کی ہے۔ ہمارے دنیا پر حکمرانی کرنے والے جانوروں کے آباء و اجداد نے اربوں سالوں سے اس وقت کے مرکزی دھارے میں آنے والے رینگنے والے جانوروں (ڈائنوسار) کے سائے میں چھپے ہوئے ان کی باقیات کو کھا لیا ، جب تک کہ ایک دن ، بلیک سوان نہیں آیا - ایک آفت نے رینگنے والے جانوروں کی بالادستی کا خاتمہ کیا …

بلیک سوان نے ہماری روز مرہ کی زندگی میں بے یقینی کو بہت گہرائی سے شامل کیا ہے۔ ایک نظریہ نگار کی حیثیت سے مجھے لگتا ہے کہ یہ دنیا جو کامل لکیروں، پیرالیپس اور نیوٹن کے قوانین سے بھری ہوئی ہے، ایک خالی شہر کی طرح ہے۔ اس کے بڑے پیمانے پر اسٹیل اور سیمنٹ نے آج بھی جدید صنعت کو سہارا دیا ہے اور یہاں تک کہ ہمیں بلیک سوان کے رازوں کو جاننے میں مدد دی ہے، لیکن ہمیں خود کو جاننے سے روک دیا ہے۔

• مکاشفہ

  • #### بلیک سوان کا چہرہ - مواقع کا سامنا کرنا:

زندہ رہنا ایک سخت عقیدہ ہے۔ ہماری ثقافت ہیروز کی حوصلہ افزائی کرتی ہے ، لیکن تاریخ زندہ بچ جانے والوں کی طرف سے لکھی جاتی ہے۔ زندہ رہنا ، دل کھولنا ، آنکھیں کھولنا ، فعال طور پر تیاری کرنا ، آپ کو اپنے سیاہ سوان کا انتظار کرنے کے لئے زیادہ مواقع ملتے ہیں۔

• #### منفی سیاہ سونا - ٹائین خطرے سے دوچار:

بلیک سوان کی خصوصیت یہ ہے کہ وہ سیاہ ہے، وہ ظاہر ہونے سے پہلے اندھیرے میں چھپا رہتا ہے، یہاں تک کہ اگر وہ آپ کے پیچھے آپ کو دیکھ رہا ہے، تو آپ کو یہ معلوم نہیں ہوسکتا ہے۔ اس کے بارے میں سوچ کر مجھے کوئی تشویش نہیں ہے۔ کیونکہ ان تمام نامعلوم خطرات میں سے کوئی بھی خطرہ نہیں ہے، حقیقی خطرہ آپ کو معلوم نہیں ہے۔

• #### خطرے کا کنٹرول:

نقصان کو روکنا۔ جب ایک منفی سیاہ سونا گرتا ہے تو ، اس کے اثرات کو مقامی طور پر محدود کرنے کے سوا کچھ نہیں کیا جاسکتا ہے اور اس سے برفانی تودے پیدا نہیں ہوتے ہیں۔

• #### تعلیمی رویہ:

اس کے باوجود ، گاس کو حقیر نہ سمجھیں ، کیوں کہ یہاں تک کہ اگر آپ کو گاس کے بارے میں کچھ معلوم ہو تو ، آپ کو اس کی قیمت معلوم ہوگی۔

ٹویٹ ایمبیڈ کریں