سات رجعت کی تکنیکوں میں آپ کو مہارت حاصل کرنی چاہئے۔

**اس مضمون میں رجعت تجزیہ اور اس کے فوائد کی وضاحت کی گئی ہے۔ اس میں سب سے زیادہ استعمال ہونے والی سات رجعت تکنیکوں اور ان کے اہم عناصر کا خلاصہ کیا گیا ہے جن پر قابو پانا چاہئے۔ ** ** ریگولیشن تجزیہ ماڈلنگ اور اعداد و شمار کا تجزیہ کرنے کا ایک اہم ذریعہ ہے۔ اس مضمون میں ریگولیشن تجزیہ کے معنی اور اس کے فوائد کی وضاحت کی گئی ہے۔ اس مضمون میں سب سے زیادہ استعمال ہونے والی ریگولیشن تکنیک اور اس کے اہم عناصر جیسے لکیری ریگولیشن ، منطقی ریگولیشن ، کثیر جہتی ریگولیشن ، مرحلہ وار ریگولیشن ، فولڈنگ ریگولیشن ، سوئنگ ریگولیشن ، اور ElasticNet ریگولیشن کا خلاصہ کیا گیا ہے۔**

• ### رجعت تجزیہ کیا ہے؟

رجعت تجزیہ (انگریزی: Regression analysis) ایک پیش گوئی کرنے والی ماڈلنگ تکنیک ہے جو اس وجہ سے متغیرات (targets) اور خود متغیرات (predictors) کے مابین تعلقات کا مطالعہ کرتی ہے۔ اس تکنیک کو عام طور پر پیش گوئی کرنے والے تجزیہ ، ٹائم سیریز ماڈل اور دریافت متغیرات کے مابین وجوہات کے مابین تعلقات کے لئے استعمال کیا جاتا ہے۔ مثال کے طور پر ، ڈرائیوروں کی لاپرواہی ڈرائیونگ اور سڑک کے ٹریفک حادثات کی تعداد کے مابین تعلقات کا مطالعہ کرنے کا بہترین طریقہ رجعت ہے۔

رجعت تجزیہ اعداد و شمار کو ماڈلنگ اور تجزیہ کرنے کا ایک اہم ذریعہ ہے۔ یہاں ، ہم ان اعداد و شمار کے پوائنٹس کو فٹ کرنے کے لئے منحنی خطوط / لائنوں کا استعمال کرتے ہیں ، اور اس طرح ، منحنی خطوط یا لائنوں سے اعداد و شمار کے پوائنٹس تک فاصلے میں فرق کم سے کم ہوتا ہے۔ میں اس کے بارے میں مزید تفصیل سے وضاحت کروں گا۔

• ### ہم رجعت تجزیہ کیوں استعمال کرتے ہیں؟

جیسا کہ اوپر بیان کیا گیا ہے ، رجعت تجزیہ دو یا زیادہ متغیرات کے مابین تعلقات کا اندازہ لگاتا ہے۔ ذیل میں ، آئیے اس کو سمجھنے کے لئے ایک آسان مثال دیں:

مثال کے طور پر، موجودہ اقتصادی حالات میں، آپ کو ایک کمپنی کی فروخت میں اضافہ کا اندازہ لگانا ہے. اب آپ کے پاس کمپنی کے تازہ ترین اعداد و شمار ہیں، جو ظاہر کرتے ہیں کہ فروخت میں اضافہ تقریباً 2.5 گنا زیادہ ہے. پھر رجعت تجزیہ کا استعمال کرتے ہوئے، ہم موجودہ اور ماضی کی معلومات کی بنیاد پر مستقبل میں کمپنی کی فروخت کا اندازہ لگا سکتے ہیں.

رجعت تجزیہ کا استعمال کرنے کے بہت سے فوائد ہیں۔ خاص طور پر:

یہ خود متغیر اور متغیر کے درمیان ایک اہم تعلق ظاہر کرتا ہے؛

اس سے ظاہر ہوتا ہے کہ ایک سے زیادہ خود متغیرات کے ایک متغیر پر اثر انداز ہونے کی شدت۔

رجعت تجزیہ ہمیں مختلف پیمانوں پر متغیرات کے مابین باہمی اثر و رسوخ کا موازنہ کرنے کی بھی اجازت دیتا ہے ، جیسے قیمتوں میں تبدیلی اور پروموشنل سرگرمیوں کی تعداد کے مابین روابط۔ یہ مارکیٹ کے محققین ، اعداد و شمار کے تجزیہ کاروں اور اعداد و شمار کے سائنسدانوں کو بہتر متغیرات کے ایک گروپ کو خارج کرنے اور ان کا اندازہ لگانے میں مددگار ثابت ہوتا ہے جس کے لئے پیش گوئی کے ماڈل تیار کیے جاسکتے ہیں۔

• ### ہمارے پاس کتنی قسم کی ریگریشن ٹکنالوجی ہے؟

مختلف قسم کی رجعت کی تکنیک پیش گوئی کے لئے استعمال کی جاتی ہیں۔ ان تکنیکوں میں بنیادی طور پر تین پیمائشیں ہیں: خود متغیر کی تعداد ، خود متغیر کی قسم اور رجعت کی لکیر کی شکل۔ ہم ان کے بارے میں ذیل میں تفصیل سے گفتگو کریں گے۔

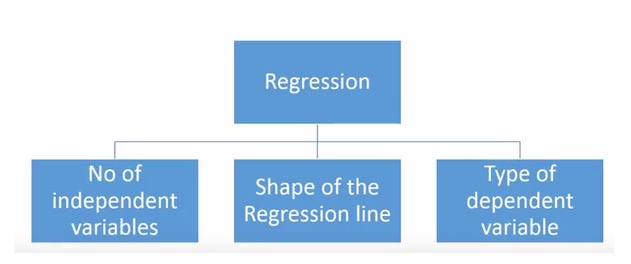
تخلیقی لوگوں کے لئے ، اگر آپ کو مندرجہ بالا پیرامیٹرز کا ایک مجموعہ استعمال کرنے کی ضرورت محسوس ہوتی ہے تو ، آپ ایک رجعت ماڈل بھی تشکیل دے سکتے ہیں جو استعمال نہیں کیا گیا ہے۔ لیکن شروع کرنے سے پہلے ، سب سے زیادہ استعمال ہونے والے رجعت کے طریقوں کے بارے میں جانیں:

• 1. لکیری رجعت

  یہ سب سے مشہور ماڈلنگ تکنیکوں میں سے ایک ہے۔ لکیری رجعت عام طور پر لوگوں کی پیش گوئی کرنے والے ماڈل سیکھنے کے لئے ترجیحی تکنیکوں میں سے ایک ہے۔ اس تکنیک میں ، رجعت کی لکیر کی نوعیت لکیری ہے کیونکہ متغیر مسلسل ہے ، خود متغیر مسلسل ہوسکتا ہے یا الگ تھلگ ہوسکتا ہے۔

  لکیری رجعت بہترین انضمام کی لکیری ((یعنی رجعت کی لکیری) کا استعمال کرتا ہے تاکہ متغیرات ((Y) اور ایک یا ایک سے زیادہ متغیرات ((X)) کے مابین ایک رشتہ قائم کیا جاسکے۔

  اس کو ایک مساوات سے بیان کریں، Y=a+b*X + e، جہاں a کٹائی ہے، b سیدھی لکیروں کا مائل ہے، اور e غلطی ہے۔ یہ مساوات ہدف متغیر کی اقدار کی پیش گوئی کر سکتی ہے، جس کی پیش گوئی کی گئی متغیر کی بنیاد پر کی جاسکتی ہے۔

  

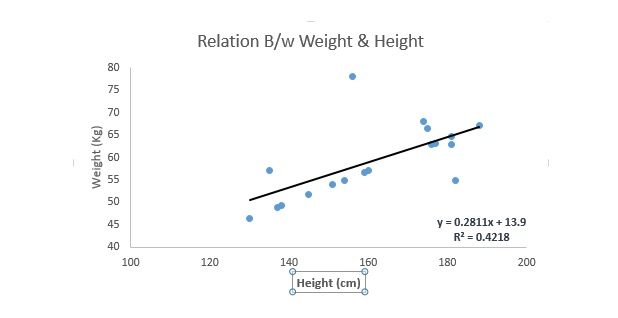
  یکطرفہ لکیری رجعت اور کثیر جہتی لکیری رجعت میں فرق یہ ہے کہ کثیر جہتی لکیری رجعت میں ((>1) خود متغیر ہوتا ہے ، جبکہ یکطرفہ لکیری رجعت میں عام طور پر صرف ایک خود متغیر ہوتا ہے۔ اب سوال یہ ہے کہ ہم ایک بہترین فٹ لائن کیسے حاصل کریں؟

  بہترین فٹ لائن (a اور b) کی قیمت کیسے حاصل کی جائے؟

  اس مسئلے کو کم سے کم دو ضرب سے آسانی سے پورا کیا جاسکتا ہے۔ کم سے کم دو ضرب بھی رجعت کی لائن کو فٹ کرنے کے لئے سب سے زیادہ استعمال ہونے والا طریقہ ہے۔ مشاہداتی اعداد و شمار کے ل it ، یہ بہترین فٹ لائن کا حساب لگانے کے لئے ہر اعداد و شمار کے نقطہ کو کم سے کم کرکے عمودی انحراف کے مربع کا مجموعہ کرتا ہے۔ چونکہ جب جمع کیا جاتا ہے تو ، انحراف پہلے مربع ہوتا ہے ، لہذا مثبت اور منفی اقدار کو آفسیٹ نہیں کیا جاتا ہے۔

  

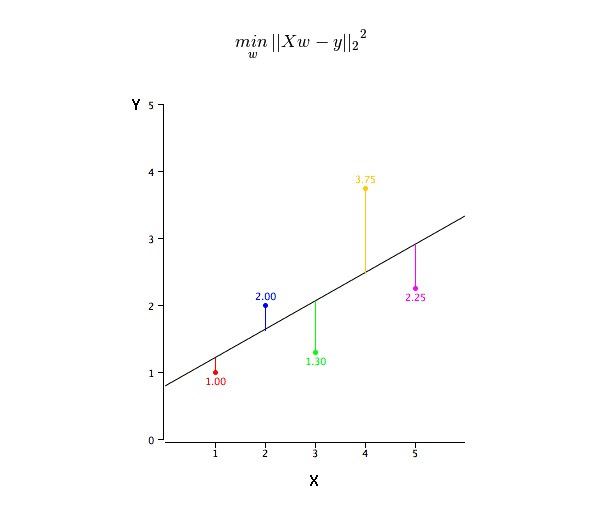
  ہم ماڈل کی کارکردگی کا اندازہ لگانے کے لئے آر اسکوائر اشارے استعمال کرسکتے ہیں۔ ان اشارے کے بارے میں مزید معلومات کے لئے ، ماڈل کی کارکردگی کے اشارے حصہ 1 ، حصہ 2 پڑھیں۔

  اہم نکات:

  • خود متغیر اور اسباب متغیر کے درمیان لکیری تعلق ہونا ضروری ہے
  • کثیر رجعت میں کثیر ہم لکیری ، خود سے متعلق اور متضاد ہے۔
  • لکیری رجعت غیر معمولی اقدار کے لئے بہت حساس ہے۔ اس سے رجعت کی لکیر پر شدید اثر پڑتا ہے ، اور آخر کار اس کی پیش گوئی کی قیمت پر اثر پڑتا ہے۔
  • کثیر کالمینیٹائزیشن کوفیکٹینٹ تخمینے کی قدر میں فرق بڑھاتا ہے، جس سے ماڈل میں معمولی تبدیلیوں کے ساتھ، تخمینے بہت حساس ہوتے ہیں۔ نتیجے کے طور پر، کوفیکٹینٹ تخمینے کی قدر غیر مستحکم ہوتی ہے
  • ایک سے زیادہ خود متغیرات کے معاملے میں ، ہم سب سے اہم خود متغیر کو منتخب کرنے کے لئے فارورڈ سلیکشن ، بیک سلیکشن اور مرحلہ وار سلیکشن کا استعمال کرسکتے ہیں۔

• لاجسٹک رجریشن 2.

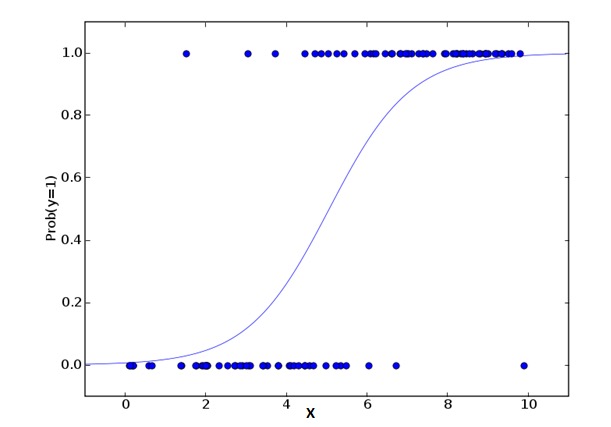
  منطقی رجعت کا استعمال اس بات کا تعین کرنے کے لئے کیا جاتا ہے کہ کس قسم کے واقعات = کامیابی اور کس قسم کے واقعات = ناکامی ہیں۔ جب متغیر کی قسم دوہری ((¹⁄₀ ، سچ / جھوٹا ، ہاں / نہیں) متغیر سے متعلق ہوتی ہے تو ، ہمیں منطقی رجعت کا استعمال کرنا چاہئے۔ یہاں ، Y کی قیمت 0 سے 1 تک ہے ، جس کو مندرجہ ذیل مساوات سے ظاہر کیا جاسکتا ہے۔

  odds= p/ (1-p) = probability of event occurrence / probability of not event occurrence
  ln(odds) = ln(p/(1-p))
  logit(p) = ln(p/(1-p)) = b0+b1X1+b2X2+b3X3....+bkXk
  

  مندرجہ بالا فارمولے میں، p کسی خاص خصوصیت کا اظہار کرنے کا امکان ظاہر کرتا ہے۔ آپ کو یہ سوال پوچھنا چاہئے کہ ہم فارمولے میں لاگ ان کیوں استعمال کرتے ہیں؟

  چونکہ ہم یہاں دوہری تقسیم کا استعمال کر رہے ہیں ((غیر متغیر کی وجہ سے) ، ہمیں اس تقسیم کے لئے بہترین منسلک فنکشن کا انتخاب کرنے کی ضرورت ہے۔ یہ لوگٹ فنکشن ہے۔ مندرجہ بالا مساوات میں ، پیرامیٹرز کو نمونے کے انتہائی متوقع تخمینے کی طرف سے منتخب کیا گیا ہے ، نہ کہ کم سے کم مربع اور غلطی (جیسا کہ عام رجعت میں استعمال ہوتا ہے) ۔

  

  اہم نکات:

  • یہ وسیع پیمانے پر درجہ بندی کے مسائل کے لئے استعمال کیا جاتا ہے.
  • منطقی رجعت کو خود متغیر اور متغیر کی وجہ سے لکیری تعلقات کی ضرورت نہیں ہے۔ یہ مختلف اقسام کے تعلقات کو سنبھال سکتا ہے کیونکہ اس نے پیش گوئی کے متعلقہ رسک انڈیکس OR پر غیر لکیری لاگ تبادلوں کا استعمال کیا ہے۔
  • ہم نے تمام اہم متغیرات کو شامل کرنا چاہئے تاکہ ہم زیادہ سے زیادہ فٹ اور غیر فٹ ہونے سے بچ سکیں۔ اس بات کو یقینی بنانے کا ایک اچھا طریقہ یہ ہے کہ منطقی واپسی کا اندازہ لگانے کے لئے مرحلہ وار فلٹرنگ کا استعمال کریں۔
  • اس کے لیے نمونے کی بڑی مقدار درکار ہوتی ہے، کیونکہ نمونے کی کم تعداد کے ساتھ، بہت زیادہ امکان ہے کہ اندازہ لگایا گیا اثر معمولی کم سے کم دوگنا سے بھی خراب ہوگا۔
  • خود متغیرات کو ایک دوسرے کے ساتھ منسلک نہیں ہونا چاہئے ، یعنی ان میں کثیر کالمینیٹیٹی نہیں ہے۔ تاہم ، تجزیہ اور ماڈلنگ میں ، ہم درجہ بندی کے متغیرات کے باہمی اثر و رسوخ کو شامل کرنے کا انتخاب کرسکتے ہیں۔
  • اگر کسی متغیر کی قدر ترتیب وار متغیر ہے تو اسے ترتیب کی منطقی واپسی کہا جاتا ہے۔
  • اگر متغیر متعدد ہے تو ، اسے کثیر منطقی واپسی کہا جاتا ہے۔

• 3. polynomial رجعت

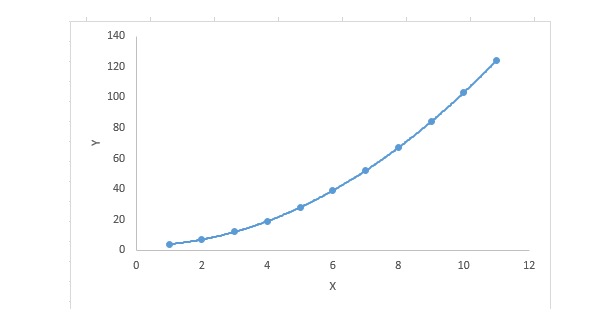
  ایک رجعت مساوات کے لئے، اگر خود متغیر کا اشاریہ 1 سے زیادہ ہے تو یہ کثیرالاضلاع رجعت مساوات ہے۔ جیسا کہ مندرجہ ذیل مساوات میں دکھایا گیا ہے:

  y=a+b*x^2
  

  اس رجعت کی تکنیک میں، بہترین فٹ لائن ایک سیدھی لائن نہیں ہے۔ بلکہ اعداد و شمار کے پوائنٹس کو فٹ کرنے کے لئے ایک منحنی خطوط ہے۔

  

  اہم نکات:

  • اگرچہ ایک حوصلہ افزائی کی جا سکتی ہے کہ ایک اعلی درجے کی کثیرالاضلاع کو فٹ کیا جا سکے اور کم غلطی حاصل کی جا سکے ، لیکن اس سے زیادہ فٹ ہونا ممکن ہے۔ آپ کو فٹ ہونے کی صورت کو دیکھنے کے لئے باقاعدگی سے رشتہ دار چارٹ تیار کرنے کی ضرورت ہے ، اور اس بات کو یقینی بنانے پر توجہ مرکوز کریں کہ فٹ مناسب ہے ، نہ ہی زیادہ فٹ اور نہ ہی کم فٹ۔ ذیل میں ایک مثال ہے جو سمجھنے میں مدد کر سکتی ہے:

  

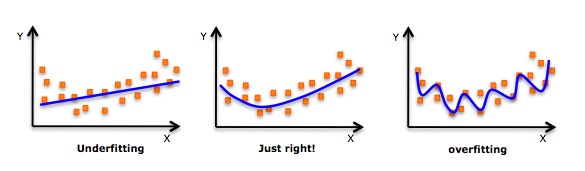
  • واضح طور پر دونوں سروں پر منحنی خطوط کی تلاش کریں اور دیکھیں کہ کیا ان شکلوں اور رجحانات کا کوئی معنی ہے۔ اعلی درجے کی کثیرالاضلاع کے نتیجے میں عجیب و غریب نتائج برآمد ہوسکتے ہیں۔

• مرحلہ وار رجعت

  جب ہم ایک سے زیادہ خود متغیر کے ساتھ کام کرتے ہیں تو ، ہم اس قسم کی واپسی کا استعمال کرسکتے ہیں۔ اس تکنیک میں ، خود متغیر کا انتخاب ایک خودکار عمل میں کیا جاتا ہے ، جس میں غیر انسانی آپریشن بھی شامل ہے۔

  یہ کارنامہ اہم متغیرات کی شناخت کے لئے اعدادوشمار کی اقدار جیسے آر اسکوائر ، ٹی اسٹیٹس اور اے آئی سی اشارے کو دیکھ کر کیا گیا ہے۔ مرحلہ وار رجعت کو ماڈل میں فٹ کرنے کے لئے ایک ہی وقت میں مخصوص معیار پر مبنی ہم آہنگی متغیرات کو شامل / حذف کرکے۔ ذیل میں کچھ عام طور پر استعمال ہونے والے مرحلہ وار رجعت کے طریقے درج ہیں:

  • معیاری تدریجی رجعت دو کام کرتی ہے۔ یعنی ہر قدم کے لئے درکار پیش گوئیوں کو شامل کرنا اور ختم کرنا۔
  • فارورڈ سلیکشن ماڈل میں سب سے نمایاں پیش گوئی سے شروع ہوتا ہے اور پھر ہر قدم کے لئے متغیرات شامل کرتا ہے۔
  • پسماندہ ہٹانے کا طریقہ ماڈل کی تمام پیش گوئیوں کے ساتھ ساتھ شروع ہوتا ہے ، اور پھر ہر قدم پر کم سے کم نمایاں متغیرات کو ختم کرتا ہے۔
  • اس ماڈلنگ تکنیک کا مقصد کم سے کم پیش گوئی متغیرات کی تعداد کا استعمال کرتے ہوئے پیش گوئی کی صلاحیت کو زیادہ سے زیادہ کرنا ہے۔ یہ بھی اعلی جہتی ڈیٹا سیٹ کے ساتھ کام کرنے کا ایک طریقہ ہے۔

• ریج رجریشن

  ریگولیشن تجزیہ ایک ایسی تکنیک ہے جس کا استعمال کثیر الاضلاع کے اعداد و شمار کے لئے کیا جاتا ہے۔ کثیر الاضلاع کے حالات میں ، اگرچہ کم سے کم ضرب دوہرا ((OLS) ہر متغیر کے لئے منصفانہ ہے ، لیکن ان میں بہت زیادہ اختلافات ہیں ، جس کی وجہ سے مشاہداتی اقدار انحراف اور حقیقی اقدار سے دور ہیں۔ ریگولیشن کو کم کرنے کے لئے ، ریگولیشن کے تخمینے میں ایک اضافی انحراف شامل کرکے معیاری غلطی کو کم کیا گیا ہے۔

  اوپر ہم نے لکیری رجعت کی مساوات دیکھی۔ یاد ہے؟ یہ اس طرح ظاہر ہوتی ہے:

  y=a+ b*x
  

  اس مساوات میں بھی ایک غلطی ہے۔ مکمل مساوات یہ ہے:

  y=a+b*x+e (error term),  [error term is the value needed to correct for a prediction error between the observed and predicted value]
  => y=a+y= a+ b1x1+ b2x2+....+e, for multiple independent variables.
  

  ایک لکیری مساوات میں ، پیش گوئی کی غلطی کو دو ذیلی حصوں میں تقسیم کیا جاسکتا ہے۔ ایک انحراف ہے ، اور دوسرا فرق ہے۔ پیش گوئی کی غلطی ان دونوں حصوں یا ان دونوں میں سے کسی ایک کی وجہ سے ہوسکتی ہے۔ یہاں ، ہم اس سے متعلق غلطیوں پر تبادلہ خیال کریں گے جو فرق کی وجہ سے پیدا ہوتی ہیں۔

  لیمبڈا ریگریشن نے کثیر کالمینیٹائزیشن کے مسئلے کو حل کرنے کے لئے کمپیکٹ پیرامیٹرز λ{\displaystyle \lambda } کا استعمال کیا ہے۔ ذیل میں فارمولہ دیکھیں۔

  

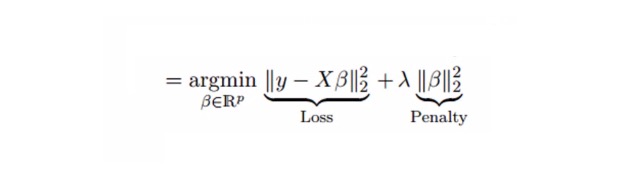
  اس فارمولے میں دو اجزاء ہیں۔ پہلا کم از کم دو ضرب ہے اور دوسرا β2 ((β - مربع) کا λ گنا ہے، جہاں β متعلقہ عنصر ہے۔ اس کو کم سے کم دو ضرب میں شامل کرنے کے لئے اس کو کم سے کم تقسیم میں شامل کیا گیا ہے۔

  اہم نکات:

  • اس رجعت کا مفروضہ کم سے کم دو ضرب رجعت کے مترادف ہے سوائے اس کے کہ اس میں مستقل اعداد ہوں؛
  • اس نے متعلقہ فیکٹر کی قدر کو کم کیا لیکن صفر تک نہیں پہنچا ، جس سے یہ ظاہر ہوتا ہے کہ اس میں خصوصیت کا انتخاب کرنے کا فنکشن نہیں ہے
  • یہ ایک باقاعدگی سے طریقہ ہے اور L2 باقاعدگی سے استعمال کیا جاتا ہے.

• 6۔ لاسسو رجعت پسندی

  اس کا استعمال کم از کم مطلق سکڑنے اور انتخاب کے آپریٹر (Lasso) کی طرف سے کیا جاتا ہے۔ یہ لکیری رجعت کی طرح ہے اور رجعت کے عنصر کی مطلق قیمت کی مقدار کو بھی سزا دیتا ہے۔ اس کے علاوہ ، یہ تبدیلی کی مقدار کو کم کرنے اور لکیری رجعت کے ماڈل کی درستگی کو بڑھانے کے قابل ہے۔ مندرجہ ذیل فارمولا دیکھیں:

  

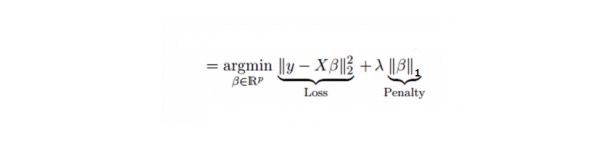
  لاسو ریگریشن ریج ریگریشن سے تھوڑا سا مختلف ہے ، جس میں سزا کا فنکشن استعمال کیا جاتا ہے جو مطلق ہے ، مربع نہیں ہے۔ اس سے سزا کا نتیجہ ہوتا ہے ((یا اس کے مساوی مطلق قدر کی رقم جس کا تخمینہ لگایا گیا ہے) کچھ پیرامیٹرز کے تخمینے کے نتائج کو صفر کے برابر بناتا ہے۔ سزا کی قدر کا استعمال کرتے ہوئے ، مزید تخمینہ لگانے سے سکڑنے والی قدر صفر کے قریب ہوجاتی ہے۔ اس سے ہمیں دیئے گئے n متغیرات میں سے متغیر کا انتخاب کرنا پڑے گا۔

  اہم نکات:

  • اس رجعت کا مفروضہ کم سے کم دو ضرب رجعت کے مترادف ہے سوائے اس کے کہ اس میں مستقل اعداد ہوں؛
  • اس کا سکڑنے کا فیکٹر صفر کے قریب ہے (یعنی صفر کے برابر) ، جو کہ خصوصیت کے انتخاب میں مدد کرتا ہے۔
  • یہ ایک باقاعدگی کا طریقہ ہے، L1 باقاعدگی کا استعمال کرتے ہوئے؛
  • اگر متغیرات کی ایک پیش گوئی کی گئی سیٹ انتہائی متعلقہ ہے تو ، لاسسو ان میں سے ایک متغیر کو منتخب کرتا ہے اور باقی کو صفر تک کم کرتا ہے۔

• 7. ElasticNet کی واپسی

  ElasticNet لاسسو اور رِج رجعت تکنیکوں کا ایک ہائبرڈ ہے۔ یہ L1 کو تربیت دینے کے لئے استعمال کرتا ہے اور L2 کو باقاعدگی سے میٹرکس کے طور پر ترجیح دیتا ہے۔ جب متعدد متعلقہ خصوصیات موجود ہیں تو ElasticNet مفید ہے۔ لاسسو ان میں سے ایک کو تصادفی طور پر منتخب کرے گا ، جبکہ ElasticNet دو کو منتخب کرے گا۔

  

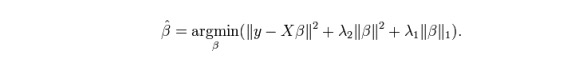
  لیسسو اور رِج کے مابین عملی فائدہ یہ ہے کہ یہ لچکدار نیٹ ورک کو لپیٹ کی حالت میں رِج کی کچھ استحکام کی وراثت کی اجازت دیتا ہے۔

  اہم نکات:

  • اس کے نتیجے میں، یہ ایک گروپ اثر پیدا کر سکتا ہے، خاص طور پر جب یہ انتہائی متعلقہ متغیرات کے ساتھ ہوتا ہے.
  • متغیرات کی تعداد کی کوئی حد نہیں ہے۔
  • یہ ڈبل کمپریشن برداشت کر سکتا ہے.
  • ان 7 سب سے زیادہ استعمال ہونے والی رجعت کی تکنیکوں کے علاوہ ، آپ کو دیگر ماڈل بھی دیکھنا چاہیں گے ، جیسے بائیشین ، ماحولیاتی اور مضبوط رجعت۔

• رجعت کے ماڈل کا انتخاب کیسے کریں؟

  جب آپ صرف ایک یا دو تکنیک جانتے ہیں تو زندگی آسان ہوجاتی ہے۔ میں جانتا ہوں کہ ایک ٹریننگ انسٹی ٹیوٹ نے اپنے طلباء کو بتایا کہ اگر نتیجہ تسلسل کا ہے تو ، لکیری رجعت کا استعمال کریں۔ اگر ثنائی ہے تو ، منطقی رجعت کا استعمال کریں۔

  کثیر قسم کے رجعت ماڈل میں ، خود متغیر اور متغیر کی قسم ، اعداد و شمار کی جہت اور اعداد و شمار کی دیگر بنیادی خصوصیات کی بنیاد پر ، سب سے موزوں تکنیک کا انتخاب کرنا بہت ضروری ہے۔ آپ کو صحیح رجعت ماڈل کا انتخاب کرنے کے لئے اہم عوامل یہ ہیں:

  اعداد و شمار کی کھوج پیش گوئی کے ماڈل کی تعمیر کا ایک لازمی حصہ ہے۔ جب مناسب ماڈل کا انتخاب کرتے ہو تو ، جیسے متغیرات کے تعلقات اور اثرات کی نشاندہی کرنا ، یہ ایک ترجیحی قدم ہونا چاہئے۔

  مختلف ماڈلز کے فوائد کے لئے زیادہ موزوں ، ہم مختلف اشارے کے پیرامیٹرز کا تجزیہ کرسکتے ہیں ، جیسے اعدادوشمار کے معنی کے پیرامیٹرز ، آر اسکوائر ، ایڈجسٹڈ آر اسکوائر ، اے آئی سی ، بی آئی سی ، اور غلطی کے عناصر ، دوسرا مالوز کا سی پی اصول ہے۔ یہ بنیادی طور پر ماڈل کو تمام ممکنہ ذیلی ماڈلز کے ساتھ موازنہ کرکے کیا جاتا ہے (یا احتیاط سے ان کا انتخاب کریں) ، آپ کے ماڈل میں ممکنہ انحراف کی جانچ پڑتال کریں۔

  کراس توثیق پیش گوئی کے ماڈل کا جائزہ لینے کا بہترین طریقہ ہے۔ یہاں ، اپنے ڈیٹا سیٹ کو دو حصوں میں تقسیم کریں (ایک تربیت اور ایک توثیق کے لئے) ۔ آپ کی پیش گوئی کی درستگی کی پیمائش کرنے کے لئے مشاہدے اور پیش گوئی کی قیمتوں کے مابین ایک سادہ مساوی فرق کا استعمال کریں۔

  اگر آپ کے ڈیٹا سیٹ میں متعدد مخلوط متغیرات ہیں تو آپ کو خود کار طریقے سے ماڈل سلیکشن کا انتخاب نہیں کرنا چاہئے کیونکہ آپ کو ایک ہی وقت میں تمام متغیرات کو ایک ہی ماڈل میں نہیں رکھنا چاہئے۔

  اس کا انحصار آپ کے مقصد پر بھی ہوگا۔ ایسے حالات ہوسکتے ہیں کہ ایک کم طاقتور ماڈل اعلی اعدادوشمار کے ماڈل کے مقابلے میں زیادہ آسانی سے قابل عمل ہو۔

  ریگریشن ریگولائزیشن کے طریقوں ((Lasso، Ridge اور ElasticNet) اعلی طول و عرض اور ڈیٹاسیٹ متغیرات کے مابین متعدد ہم آہنگی کے ساتھ اچھی طرح سے کام کرتے ہیں۔

سی ایس ڈی این سے نقل کیا گیا