Naive Bayes کی دلچسپ تفہیم

NavieBayes

  زندگی کے بہت سارے مواقع میں درجہ بندی کی ضرورت ہوتی ہے ، جیسے خبروں کی درجہ بندی ، مریضوں کی درجہ بندی وغیرہ۔ آپ کو تصوراتی سمجھنے کے ل this ، اس مضمون میں عملی اطلاق سے شروع ہونے والے ایک سادہ عام طور پر استعمال ہونے والے درجہ بندی کے الگورتھم کا تعارف کرایا گیا ہے۔

• 01 مریضوں کی درجہ بندی کی مثالیں

آئیے ایک مثال کے ساتھ شروع کرتے ہیں، آپ دیکھیں گے کہ بیس درجہ بندی کرنے والا بہت اچھا ہے، کوئی مشکل نہیں۔ ایک ہسپتال نے صبح میں چھ مریضوں کو داخلہ دیا، جیسا کہ ذیل میں ٹیبل میں دیکھا گیا ہے۔

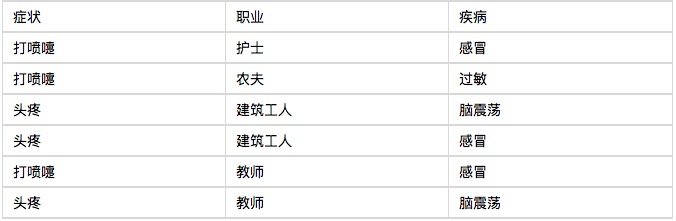
اب ساتواں مریض آیا ہے، ایک چھینکنے والا تعمیراتی مزدور۔ اس سے پوچھیں کہ اس کے سردی لگنے کا امکان کتنا ہے؟

  P(A|B) = P(B|A) P(A) / P(B)

کیا یہ ممکن ہے؟

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏x建筑工人|感冒) x P(感冒) 
  　　　　/ P(打喷嚏x建筑工人)

فرض کریں کہ چھینکنے اور تعمیراتی مزدور کی خصوصیات الگ الگ ہیں، تو یہ مساوات

  P(感冒|打喷嚏x建筑工人) 
  　　　　= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒)
  　　　　/ P(打喷嚏) x P(建筑工人)

یہ قابل شمار ہے۔

  P(感冒|打喷嚏x建筑工人) 
  　　　　= 0.66 x 0.33 x 0.5 / 0.5 x 0.33 
  　　　　= 0.66

اس کے نتیجے میں ، اس چھینکنے والے تعمیراتی کارکن کے لئے 66 فیصد امکان ہے کہ اسے سردی لگ گئی ہو۔ اسی طرح ، اس مریض کے لئے الرجی یا دماغی جھٹکے کا امکان بھی شمار کیا جاسکتا ہے۔ ان امکانات کا موازنہ کرنے سے یہ معلوم ہوتا ہے کہ اس کی بیماری کا سب سے زیادہ امکان کیا ہے۔

بیس درجہ بندی کا بنیادی طریقہ یہ ہے کہ اعداد و شمار کی بنیاد پر، بعض خصوصیات کے مطابق، ہر قسم کے امکانات کا حساب لگایا جائے، تاکہ درجہ بندی کی جا سکے.

• 02 سادہ Bayes کی درجہ بندی کے لئے فارمولہ

فرض کریں کہ کسی فرد میں n خصوصیات ہیں ، F1 ، F2 ، … ، Fn۔ موجودہ m زمرہ جات ہیں ، C1 ، C2 ، … ، Cm۔ بیسس درجہ بندی وہ درجہ بندی ہے جس کا سب سے زیادہ امکان ہے ، یعنی اس حساب کتاب کی زیادہ سے زیادہ قیمت:

  P(C|F1F2...Fn) 
  　　   = P(F1F2...Fn|C)P(C) / P(F1F2...Fn)

چونکہ P ((F1F2…Fn) تمام زمروں کے لئے ایک ہی ہے، اس کو چھوڑ دیا جا سکتا ہے، اور سوال سوال بن جاتا ہے

  P(F1F2...Fn|C)P(C)

زیادہ سے زیادہ

سادہ Bayes کی درجہ بندی ایک قدم آگے ہے، یہ فرض ہے کہ تمام خصوصیات ایک دوسرے سے آزاد ہیں، اور اس وجہ سے

  P(F1F2...Fn|C)P(C) 
  　　   = P(F1|C)P(F2|C) ... P(Fn|C)P(C)

ہر ایک عنصر کے دائیں طرف کے مساوات کو اعداد و شمار سے حاصل کیا جاسکتا ہے ، جس سے ہر زمرے کے مماثل امکانات کا حساب لگایا جاسکتا ہے ، اور اس طرح سب سے زیادہ امکان والا زمرہ معلوم کیا جاسکتا ہے۔

اگرچہ یہ فرض ہے کہ ‘تمام خصوصیات ایک دوسرے سے آزاد ہیں’ ، حقیقت میں اس کا امکان نہیں ہے ، لیکن اس سے حساب کتاب کو بہت آسان بنایا جاسکتا ہے ، اور تحقیق سے پتہ چلتا ہے کہ درجہ بندی کے نتائج کی درستگی پر اس کا کوئی اثر نہیں پڑتا ہے۔

سادہ Bayes کی درجہ بندی کا استعمال کرتے ہوئے کس طرح دیکھنے کے لئے دو مزید مثالیں ذیل میں.

• 03 اکاؤنٹس کی درجہ بندی

ایک کمیونٹی کی ویب سائٹ کے مطابق اس سائٹ پر موجود 10،000 اکاؤنٹس میں سے 89 فیصد حقیقی ہیں (سی 0) اور 11 فیصد جعلی ہیں (سی 1) ۔ اس کے بعد ، اعدادوشمار کا استعمال کرتے ہوئے ، ایک اکاؤنٹ کی صداقت کا اندازہ لگایا جاسکتا ہے۔

  C0 = 0.89 C1 = 0.11

فرض کریں کہ ایک اکاؤنٹ میں درج ذیل تین خصوصیات ہیں: F1: لاگ ان کی تعداد / رجسٹریشن کے دن F2: دوستوں کی تعداد / رجسٹریشن کے دن F3: کیا حقیقی ہیڈلائٹ استعمال کیا جائے گا (جیسے حقیقی ہیڈلائٹ 1 ہے ، غیر حقیقی ہیڈلائٹ 0 ہے) F1 = 0.1  F2 = 0.2  F3 = 0

براہ کرم بتائیں کہ یہ اکاؤنٹ اصلی ہے یا جعلی؟ اس کا طریقہ یہ ہے کہ سادہ بییسس کی درجہ بندی کا استعمال کرکے مندرجہ ذیل حساب کتاب کی قدر کا حساب لگائیں:

P(F1|C)P(F2|C)P(F3|C)P©

اگرچہ یہ اعداد و شمار اعداد و شمار سے حاصل کیے جا سکتے ہیں، لیکن یہاں ایک مسئلہ ہے: F1 اور F2 مسلسل متغیر ہیں، کسی خاص قدر کے مطابق امکانات کا حساب لگانا مناسب نہیں ہے۔ ایک چال یہ ہے کہ مسلسل اقدار کو متفرق اقدار میں تبدیل کرکے، وقفے کے امکانات کا حساب لگانا ہے۔ مثال کے طور پر F1 کو تقسیم کرنا[0, 0.05]、(0.05, 0.2)、[0.2، +∞] تین خانوں میں، پھر ہر خانے کا امکان حساب لگائیں۔ ہمارے مثال میں، F1 0.1 کے برابر ہے، جو دوسرے خانے میں آتا ہے، لہذا حساب کرتے وقت، دوسرے خانے کا امکان استعمال کیا جاتا ہے۔

اعداد و شمار کے مطابق:

P(F1|C0) = 0.5, P(F1|C1) = 0.1  P(F2|C0) = 0.7, P(F2|C1) = 0.2  P(F3|C0) = 0.2, P(F3|C1) = 0.9

اس لیے

P(F1|C0) P(F2|C0) P(F3|C0) P(C0)  = 0.5 x 0.7 x 0.2 x 0.89  = 0.0623 P(F1|C1) P(F2|C1) P(F3|C1) P(C1)  = 0.1 x 0.2 x 0.9 x 0.11  = 0.00198 اس صارف کے اکاؤنٹ کی اصلیت کا اندازہ لگانے کے لیے اس کی تصویر کا استعمال کیا گیا ہے۔ اس صارف کے اکاؤنٹ کی اصلیت کا اندازہ لگانے کے لیے اس کا استعمال کیا گیا ہے۔

• 04 صنف کی درجہ بندی

ذیل میں انسانی جسم کی خصوصیات کے اعدادوشمار ہیں۔

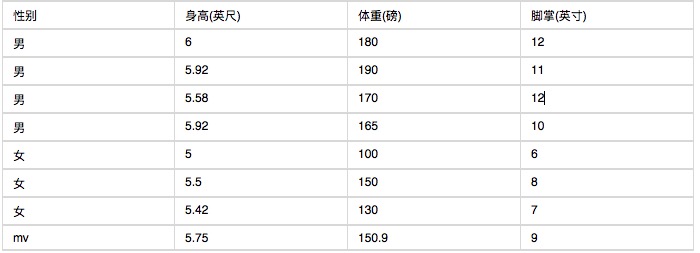
اگر کوئی شخص 6 فٹ لمبا ، 130 پونڈ وزنی اور 8 انچ قد کا ہے تو ، کیا یہ مرد یا عورت ہے؟ اس فارمولے کی قدر کو سادہ بیسس درجہ بندی کے مطابق حساب لگائیں۔

P (لمبائی اور جنس) x P (وزن اور جنس) x P (پاؤں اور ہاتھ اور جنس) x P (جنس)

یہاں کی مشکل یہ ہے کہ چونکہ قد، وزن اور پاؤں کی ہتھیلی مسلسل متغیرات ہیں، اس لیے اس کا حساب لگانے کے لیے الگ الگ متغیرات کا استعمال نہیں کیا جا سکتا۔ اور چونکہ نمونے بہت کم ہیں، اس لیے اس کا حساب لگانے کے لیے وقفہ نہیں کیا جا سکتا۔ اس وقت کیا کیا جا سکتا ہے؟ اس وقت یہ فرض کیا جا سکتا ہے کہ مردوں اور عورتوں کی قد، وزن اور پاؤں کی ہتھیلیاں صحیح تقسیم ہیں، اور نمونے کے ذریعے اوسط اور فرق کا حساب لگایا جا سکتا ہے، یعنی صحیح تقسیم شدہ کثافت کا فنکشن ملتا ہے۔ کثافت کا فنکشن ہونے کی صورت میں، اس قدر کو شامل کیا جا سکتا ہے اور کسی خاص مقام پر کثافت کے فنکشن کی قدر کا حساب لگایا جا سکتا ہے۔ مثال کے طور پر، مردوں کی اوسط قد 5.855 ہے، فرق 0.035 کی صحیح تقسیم ہے۔ اس لیے مردوں کی قد 6 فٹ کے پیمانے کا تناسب 1.5789 کے برابر ہے۔ (یہ 1 سے زیادہ نہیں ہے، کیونکہ یہاں کثافت کا فنکشن صرف انفرادی امکانات کی نمائندگی کرنے کے لیے استعمال کیا جاتا ہے۔)

یہ اعداد و شمار آپ کو صنف کی درجہ بندی کا حساب کرنے کی اجازت دیتے ہیں۔

P (اونچائی = 6 مرد) x P (وزن = 130 مرد) x P (پاؤں = 8 مرد) x P (مرد)

= 6.1984 x e-9

P (اونچائی = 6 مردہ خواتین) x P (وزن = 130 مردہ خواتین) x P (پاؤں = 8 مردہ خواتین) x P (خواتین)

= 5.3778 x e-4

اس کے علاوہ ، یہ بھی دیکھا جاسکتا ہے کہ خواتین مردوں کے مقابلے میں تقریبا 10،000 گنا زیادہ امکان رکھتی ہیں ، لہذا اس شخص کو ایک عورت قرار دیا جاسکتا ہے۔

ویکیپیڈیا عوامی نمبر سے نقل کیا گیا