پچھلے مضمون میں آرڈر کی آمد کے وقفے کا مطالعہ کیا گیا تھا اور یہ ظاہر کیا گیا تھا کہ ہمیں پیرامیٹرز کو متحرک طور پر ایڈجسٹ کرنے کی ضرورت کیوں ہے اور تخمینہ کے معیار کو کیسے جانچنا ہے۔ یہ مضمون گہرائی سے ڈیٹا پر توجہ مرکوز کرے گا اور درمیانی قیمت کا مطالعہ کرے گا (جسے مناسب قیمت، مائیکرو پرائس وغیرہ بھی کہا جاتا ہے)۔

گہرائی کا ڈیٹا

Binance بہترین قیمتوں کا تاریخی ڈیٹا ڈاؤن لوڈ فراہم کرتا ہے، بشمول best_bid_price: بہترین بولی کی قیمت، یعنی زیادہ سے زیادہ بولی کی قیمت، best_bid_qty: بہترین بولی کی قیمت کی تعداد، best_ask_price: بہترین پوچھنے کی قیمت، best_ask_qty: بہترین پوچھنے کی قیمت کی تعداد , transaction_time: timestamp. اس ڈیٹا میں دوسرے درجے اور گہرے زیر التواء آرڈرز شامل نہیں ہیں۔ 7 اگست کو مارکیٹ کی صورت حال کا تجزیہ کیا گیا ہے۔

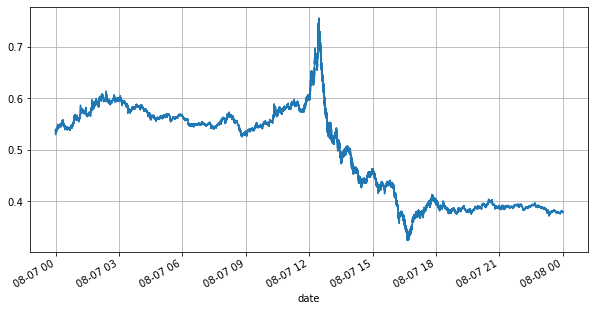
سب سے پہلے، اس دن کے بازار کو دیکھتے ہیں، اس کے علاوہ، مارکیٹ کے اتار چڑھاو کے ساتھ بہت زیادہ تبدیلی آئی ہے فروخت کی قیمت اور خرید قیمت) نے مارکیٹ کی اتار چڑھاؤ کی صورتحال کو نمایاں طور پر دکھایا ہے۔ اس دن YGG کی مارکیٹ کے اعداد و شمار کے مطابق، اس دور میں جب مختلف روبوٹس مارکیٹ میں مقابلہ کرتے ہیں، اس وقت 20% پھیلاؤ بہت کم ہے۔

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

books = pd.read_csv('YGGUSDT-bookTicker-2023-08-07.csv')

tick_size = 0.0001

books['date'] = pd.to_datetime(books['transaction_time'], unit='ms')
books.index = books['date']

books['spread'] = round(books['best_ask_price'] - books['best_bid_price'],4)

books['best_bid_price'][::10].plot(figsize=(10,5),grid=True);

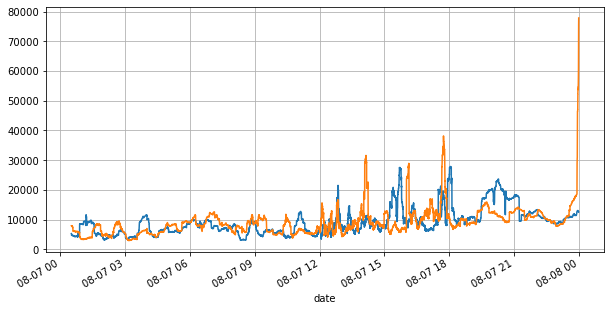
books['best_bid_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);
books['best_ask_qty'][::10].rolling(10000).mean().plot(figsize=(10,5),grid=True);

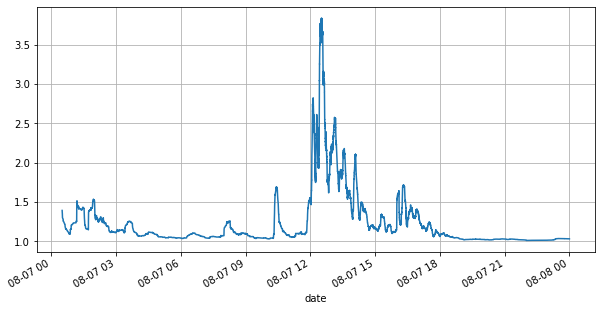
(books['spread'][::10]/tick_size).rolling(10000).mean().plot(figsize=(10,5),grid=True);

books['spread'].value_counts()[books['spread'].value_counts()>500]/books['spread'].value_counts().sum()

0.0001    0.799169
0.0002    0.102750
0.0003    0.042472
0.0004    0.022821
0.0005    0.012792
0.0006    0.007350
0.0007    0.004376
0.0008    0.002712
0.0009    0.001657
0.0010    0.001089
0.0011    0.000740
0.0012    0.000496
0.0013    0.000380
0.0014    0.000258
0.0015    0.000197
0.0016    0.000140
0.0017    0.000112
0.0018    0.000088
0.0019    0.000063
Name: spread, dtype: float64

غیر متوازن اقتباسات

مندرجہ بالا سے، ہم دیکھ سکتے ہیں کہ خرید و فروخت کے آرڈرز کی مقدار زیادہ تر وقت میں بہت مختلف ہوتی ہے، اس فرق کا مارکیٹ کے قلیل مدتی حالات پر ایک مضبوط پیشن گوئی اثر پڑتا ہے۔ وجہ پچھلے مضمون میں بتائی گئی وجہ سے ملتی جلتی ہے کہ چھوٹے خرید آرڈرز اکثر کمی کا باعث بنتے ہیں۔ اگر ایک طرف زیر التواء آرڈرز دوسری طرف کے آرڈرز کے مقابلے میں نمایاں طور پر چھوٹے ہیں، اور یہ فرض کرتے ہوئے کہ خرید و فروخت کے فعال آرڈرز کی مقدار قریب ہے، تو چھوٹے زیر التواء آرڈرز والی طرف کے ختم ہونے کا امکان زیادہ ہوگا، اس طرح قیمت بڑھ جائے گی۔ تبدیلیاں غیر متوازن اقتباسات کی نمائندگی I کرتے ہیں: 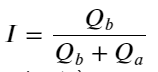جہاں Q_b خرید آرڈر کی مقدار (best_bid_qty) کی نمائندگی کرتا ہے، اور Q_a فروخت آرڈر کی مقدار (best_ask_qty) کی نمائندگی کرتا ہے۔

درمیانی قیمت کی وضاحت کریں: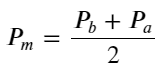

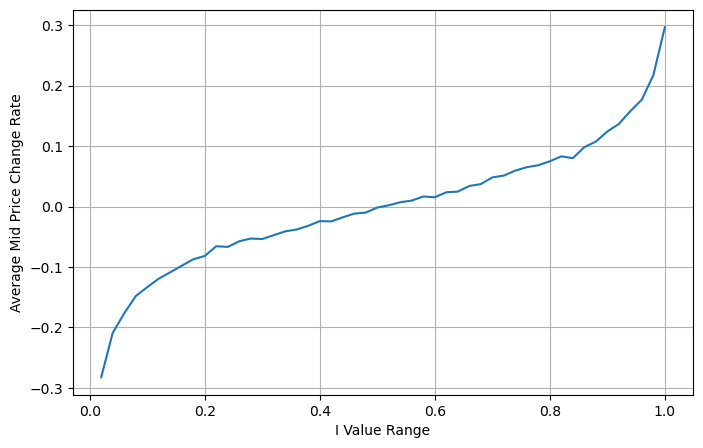
مندرجہ ذیل اعداد و شمار اگلے وقفے میں درمیانی قیمت کی تبدیلی کی شرح اور عدم توازن I کے درمیان تعلق کو ظاہر کرتا ہے۔ جیسا کہ توقع ہے، جیسا کہ I میں اضافہ ہوتا ہے، قیمت میں اضافے کا امکان زیادہ ہوتا ہے اور یہ 1 کے قریب ہوتا ہے، اس کی شدت قیمت کی تبدیلی بھی تیز ہے. ہائی فریکوئنسی ٹریڈنگ میں، درمیانی قیمت کو متعارف کرانے کا مقصد مستقبل کی قیمتوں میں ہونے والی تبدیلیوں کی بہتر پیش گوئی کرنا ہے، دوسرے لفظوں میں، مستقبل کی قیمت سے جتنا کم فرق ہوتا ہے، درمیانی قیمت اتنی ہی بہتر ہوتی ہے۔ ظاہر ہے، زیر التواء آرڈرز کا عدم توازن حکمت عملی کی پیشین گوئی کے لیے اضافی معلومات فراہم کرتا ہے، اس کو مدنظر رکھتے ہوئے، ہم وزنی درمیانی قیمت کی وضاحت کرتے ہیں:

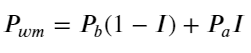
books['I'] = books['best_bid_qty'] / (books['best_bid_qty'] + books['best_ask_qty'])

books['mid_price'] = (books['best_ask_price'] + books['best_bid_price'])/2

bins = np.linspace(0, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['price_change'] = (books['mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Average Mid Price Change Rate');
plt.grid(True)

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['weighted_price_change'].mean()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

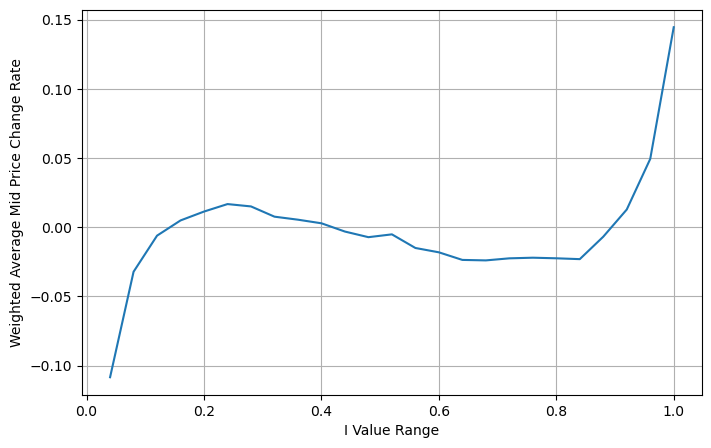
وزنی درمیانی قیمت کی ایڈجسٹمنٹ

اعداد و شمار سے، ہم دیکھ سکتے ہیں کہ وزنی درمیانی قیمت مختلف I سے بہت کم بدلتی ہے، جس کا مطلب ہے کہ وزنی درمیانی قیمت ایک بہتر فٹ ہے۔ لیکن اب بھی کچھ معمولات ہیں، جیسے کہ 0.2 اور 0.8 کے ارد گرد، جہاں انحراف نسبتاً زیادہ ہیں۔ اس سے ظاہر ہوتا ہے کہ میں اب بھی اضافی معلومات فراہم کر سکتا ہوں۔ چونکہ وزنی درمیانی قیمت یہ سمجھتی ہے کہ قیمت کی اصلاح کی اصطلاح I کے ساتھ مکمل طور پر لکیری ہے، یہ واضح طور پر درست نہیں ہے جیسا کہ اوپر والے اعداد و شمار سے دیکھا جا سکتا ہے، جب I 0 اور 1 کے قریب ہوتا ہے، انحراف تیز ہوتا ہے اور یہ ایک نہیں ہے۔ لکیری رشتہ

مزید بدیہی نظر کے لیے، میری یہاں نئی ​​تعریف کی گئی ہے:

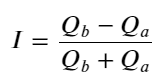
اس وقت:

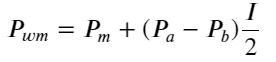
اس فارم کا مشاہدہ کرتے ہوئے، ہم یہ جان سکتے ہیں کہ وزنی درمیانی قیمت اوسط درمیانی قیمت کی درستگی ہے، اور اصلاح کی اصطلاح I کا ایک فعل ہے۔ یہ رشتہ I/2 ہے۔ اس وقت، I (-1,1) کی ایڈجسٹ ڈسٹری بیوشن کا فائدہ I اصل کے بارے میں ہم آہنگ ہے، جو ہمارے لیے فنکشن کے موزوں تعلق کو تلاش کرنا آسان بناتا ہے۔ گراف کا مشاہدہ کریں، اس فنکشن کو I کی طاق طاقت کے رشتے کو پورا کرنا چاہیے، جو کہ دونوں اطراف کی تیز رفتار ترقی کے ساتھ مطابقت رکھتا ہے اور اس کے علاوہ، یہ بھی دیکھا جا سکتا ہے کہ اصل کے قریب قدر لکیری کے قریب ہے۔ اور جب میں 0 ہوتا ہے تو فنکشن کا نتیجہ 0 ہوتا ہے، اور جب میں 1 ہوتا ہے تو فنکشن کا نتیجہ 0.5 ہوتا ہے۔ تو اندازہ لگائیں کہ یہ فنکشن ایسا لگتا ہے:

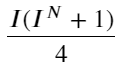
یہاں N ایک مثبت جفت عدد ہے اصل جانچ کے بعد، یہ بہتر ہے جب N 8 ہو۔ اب تک، یہ مضمون ایک نظر ثانی شدہ وزنی درمیانی قیمت کی تجویز کرتا ہے:

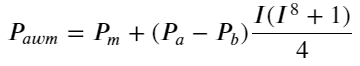
اس مقام پر، پیش گوئی کی گئی درمیانی قیمت میں تبدیلی کا بنیادی طور پر I سے کوئی تعلق نہیں ہے۔ اگرچہ یہ نتیجہ سادہ وزنی درمیانی قیمت سے بہتر ہے، لیکن اسے اصل تجارت میں لاگو نہیں کیا جا سکتا، یہ صرف ایک خیال ہے۔ S Stoikov کے 2017 کے مضمون نے مارکوف چین کا طریقہ متعارف کرایاMicro-Price، اور متعلقہ کوڈ دیتا ہے، آپ اس کا مطالعہ بھی کر سکتے ہیں۔

books['I'] = (books['best_bid_qty'] - books['best_ask_qty']) / (books['best_bid_qty'] + books['best_ask_qty'])

books['weighted_mid_price'] = books['mid_price'] + books['spread']*books['I']/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['weighted_price_change'] = (books['weighted_mid_price'].pct_change()/tick_size).shift(-1)
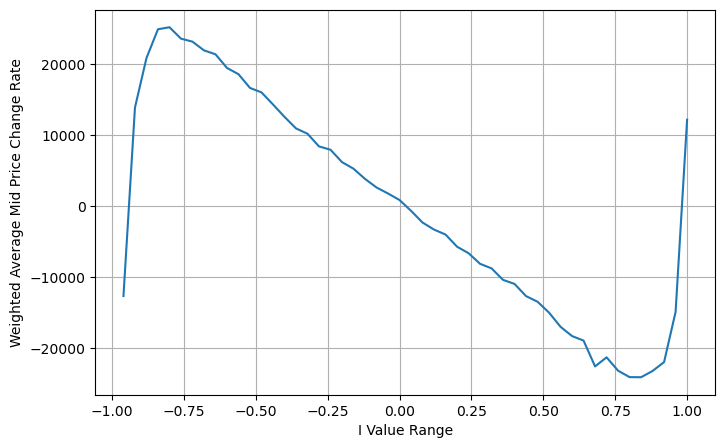
avg_change = books.groupby('I_bins')['weighted_price_change'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

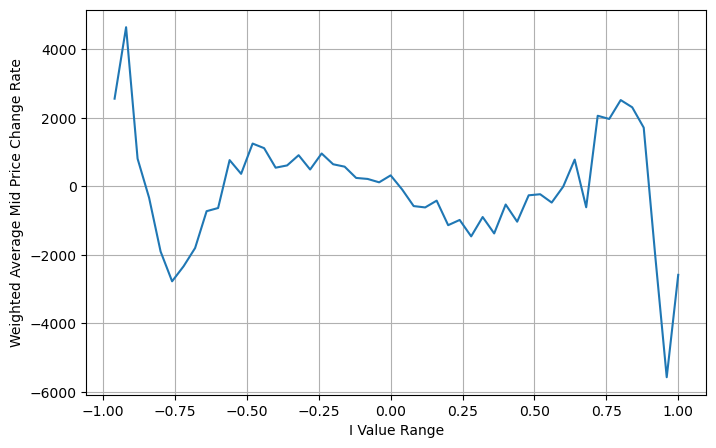
books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I'])*(books['I']**8+1)/4
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

books['adjust_mid_price'] = books['mid_price'] + books['spread']*(books['I']**3)/2
bins = np.linspace(-1, 1, 51)
books['I_bins'] = pd.cut(books['I'], bins, labels=bins[1:])
books['adjust_mid_price'] = (books['adjust_mid_price'].pct_change()/tick_size).shift(-1)
avg_change = books.groupby('I_bins')['adjust_mid_price'].sum()
plt.figure(figsize=(8,5))
plt.plot(avg_change)
plt.xlabel('I Value Range')
plt.ylabel('Weighted Average Mid Price Change Rate');
plt.grid(True)

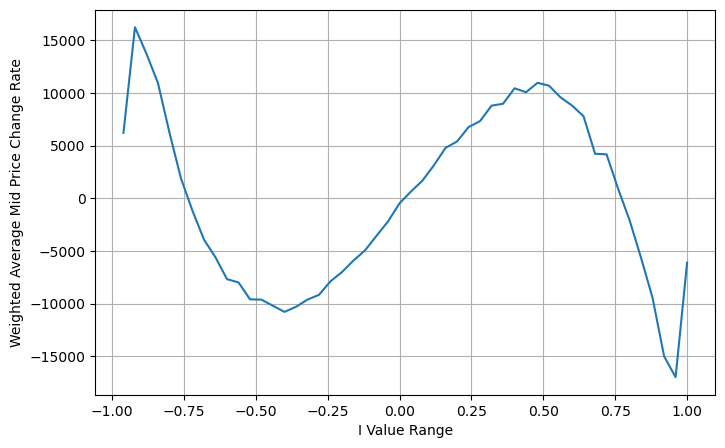
خلاصہ کریں۔

درمیانی قیمت اعلی تعدد کی حکمت عملیوں کے لیے بہت اہم ہے یہ مستقبل کی مختصر مدت کی قیمتوں کی پیشین گوئی ہے، لہذا درمیانی قیمت زیادہ سے زیادہ درست ہونی چاہیے۔ اوپر متعارف کرائی گئی درمیانی قیمتیں مارکیٹ کے اعداد و شمار پر مبنی ہیں، کیونکہ تجزیہ میں صرف ایک مارکیٹ کی قیمت استعمال کی گئی ہے۔ حقیقی تجارت میں، حکمت عملی کو ہر ممکن حد تک تمام ڈیٹا استعمال کرنا چاہیے، خاص طور پر جب حقیقی ٹریڈنگ میں تجارتی تبادلے ہوں، اور درمیانی قیمت کی پیشین گوئی کو لین دین کی اصل قیمت سے جانچنا چاہیے۔ مجھے یاد ہے کہ Stoikov نے ایک ٹویٹ پوسٹ کیا تھا جس میں کہا گیا تھا کہ اصل درمیانی قیمت خرید و فروخت کے لین دین کے امکان کا وزنی اوسط ہونا چاہیے اس مسئلے کا ابھی پچھلے مضمون میں مطالعہ کیا گیا ہے۔ محدود جگہ کی وجہ سے ان مسائل پر اگلے مضمون میں تفصیل سے بات کی جائے گی۔