پچھلے مضمون میں مختلف درمیانی قیمتوں کے حساب کتاب کے طریقوں کا ابتدائی تعارف دیا گیا تھا اور درمیانی قیمت پر نظرثانی کی گئی تھی۔

مطلوبہ ڈیٹا

آرڈر فلو ڈیٹا اور ڈیپتھ ڈیٹا کے دس درجات حقیقی ٹریڈنگ سے جمع کیے جاتے ہیں، اور اپ ڈیٹ فریکوئنسی 100ms ہے۔ حقیقی مارکیٹ میں صرف خرید و فروخت کا ڈیٹا ہوتا ہے، جسے حقیقی وقت میں اپ ڈیٹ کیا جاتا ہے، اس وقت اس کا استعمال نہیں کیا جاتا ہے۔ اس بات کو مدنظر رکھتے ہوئے کہ ڈیٹا بہت بڑا ہے، گہرائی والے ڈیٹا کی صرف 100,000 قطاریں برقرار ہیں، اور ہر سطح کے لیے مارکیٹ کے حالات کو بھی الگ الگ کالموں میں الگ کیا گیا ہے۔

from datetime import date,datetime
import time
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import ast
%matplotlib inline

tick_size = 0.0001

trades = pd.read_csv('YGGUSDT_aggTrade.csv',names=['type','event_time', 'agg_trade_id','symbol', 'price', 'quantity', 'first_trade_id', 'last_trade_id',
       'transact_time', 'is_buyer_maker'])

trades = trades.groupby(['transact_time','is_buyer_maker']).agg({
    'transact_time':'last',
    'agg_trade_id': 'last',
    'price': 'first',
    'quantity': 'sum',
    'first_trade_id': 'first',
    'last_trade_id': 'last',
    'is_buyer_maker': 'last',
})

trades.index = pd.to_datetime(trades['transact_time'], unit='ms')
trades.index.rename('time', inplace=True)
trades['interval'] = trades['transact_time'] - trades['transact_time'].shift()

depths = pd.read_csv('YGGUSDT_depth.csv',names=['type','event_time', 'transact_time','symbol', 'u1', 'u2', 'u3', 'bids','asks'])

depths = depths.iloc[:100000]

depths['bids'] = depths['bids'].apply(ast.literal_eval).copy()
depths['asks'] = depths['asks'].apply(ast.literal_eval).copy()

def expand_bid(bid_data):
    expanded = {}
    for j, (price, quantity) in enumerate(bid_data):
        expanded[f'bid_{j}_price'] = float(price)
        expanded[f'bid_{j}_quantity'] = float(quantity)
    return pd.Series(expanded)
def expand_ask(ask_data):
    expanded = {}
    for j, (price, quantity) in enumerate(ask_data):
        expanded[f'ask_{j}_price'] = float(price)
        expanded[f'ask_{j}_quantity'] = float(quantity)
    return pd.Series(expanded)
# 应用到每一行，得到新的df
expanded_df_bid = depths['bids'].apply(expand_bid)
expanded_df_ask = depths['asks'].apply(expand_ask)
# 在原有df上进行扩展
depths = pd.concat([depths, expanded_df_bid, expanded_df_ask], axis=1)

depths.index = pd.to_datetime(depths['transact_time'], unit='ms')
depths.index.rename('time', inplace=True);

trades = trades[trades['transact_time'] < depths['transact_time'].iloc[-1]]

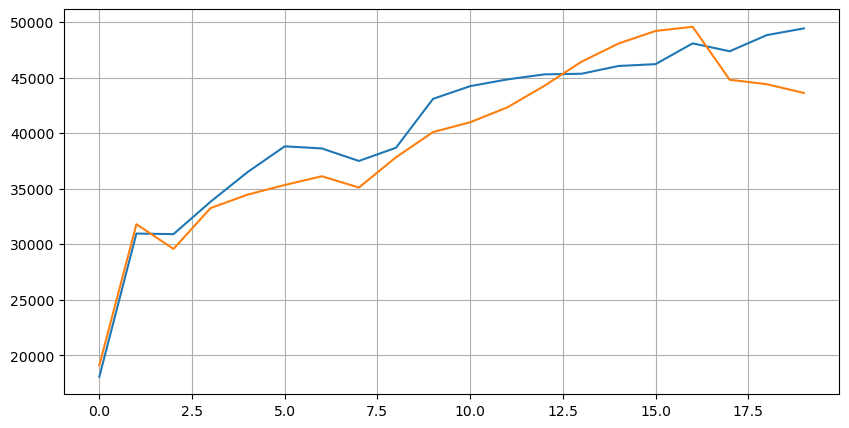
آئیے پہلے ان 20 مارکیٹوں کی تقسیم پر نظر ڈالتے ہیں جو کہ مارکیٹ کے آغاز سے جتنا دور ہے، اتنے ہی زیادہ زیر التواء آرڈرز ہیں، اور خرید و فروخت کے آرڈرز تقریباً ہم آہنگ ہیں۔

bid_mean_list = []
ask_mean_list = []
for i in range(20):
    bid_mean_list.append(round(depths[f'bid_{i}_quantity'].mean(),0))
    ask_mean_list.append(round(depths[f'ask_{i}_quantity'].mean(),0))
plt.figure(figsize=(10, 5))
plt.plot(bid_mean_list);
plt.plot(ask_mean_list);
plt.grid(True)

پیشن گوئی کی درستگی کی تشخیص کو آسان بنانے کے لیے گہرائی کے ڈیٹا اور لین دین کے ڈیٹا کو یکجا کریں۔ یہاں ہم اس بات کو یقینی بناتے ہیں کہ لین دین کے اعداد و شمار گہرائی کے اعداد و شمار کے بعد کے ہیں، بغیر تاخیر پر غور کیے، ہم پیش گوئی کی گئی قیمت اور لین دین کی اصل قیمت کے درمیان اوسط مربع غلطی کا براہ راست حساب لگاتے ہیں۔ پیشین گوئیوں کی درستگی کی پیمائش کے لیے استعمال کیا جاتا ہے۔

نتائج سے اندازہ لگاتے ہوئے، درمیانی_قیمت کی خرابی، خرید فروخت کی جوڑی کی اوسط، سب سے بڑی ہے weight_mid_price میں تبدیل ہونے کے بعد، غلطی فوری طور پر بہت چھوٹی ہو جاتی ہے، اور وزنی درمیانی قیمت کو ایڈجسٹ کرکے اسے مزید بہتر کیا جاتا ہے۔ کل کے مضمون کے شائع ہونے کے بعد، کچھ لوگوں نے اطلاع دی کہ انہوں نے صرف I^³⁄₂ کا استعمال کیا، میں نے اسے یہاں چیک کیا اور پایا کہ نتیجہ بہتر تھا۔ وجہ کے بارے میں سوچنے کے بعد، یہ واقعات کی فریکوئنسی میں فرق ہونا چاہیے جب میں -1 اور 1 کے قریب ہوتا ہے، یہ ایک کم امکانی واقعہ ہوتا ہے تاکہ ان کم امکانات کو درست کیا جا سکے۔ اس لیے زیادہ درست نہیں ہے، زیادہ تعدد والے واقعات کا خیال رکھنے کے لیے، میں نے کچھ ایڈجسٹمنٹ کیے ہیں (یہ خالصتاً تجرباتی پیرامیٹرز ہیں، اور حقیقی تجارت کے لیے زیادہ مفید نہیں ہیں):

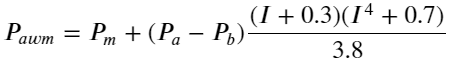
نتیجہ قدرے بہتر تھا۔ جیسا کہ پچھلے مضمون میں ذکر کیا گیا ہے، زیادہ گہرائی اور آرڈر کی تکمیل کے اعداد و شمار کے ساتھ حکمت عملیوں کی پیش گوئی کی جانی چاہیے، جو بہتری مارکیٹ کی قیمت کے ساتھ الجھ کر حاصل کی جا سکتی ہے وہ پہلے ہی بہت کمزور ہے۔

df = pd.merge_asof(trades, depths, on='transact_time', direction='backward')

df['spread'] = round(df['ask_0_price'] - df['bid_0_price'],4)
df['mid_price'] = (df['bid_0_price']+ df['ask_0_price']) / 2
df['I'] = (df['bid_0_quantity'] - df['ask_0_quantity']) / (df['bid_0_quantity'] + df['ask_0_quantity'])
df['weight_mid_price'] = df['mid_price'] + df['spread']*df['I']/2
df['adjust_mid_price'] = df['mid_price'] + df['spread']*(df['I'])*(df['I']**8+1)/4
df['adjust_mid_price_2'] = df['mid_price'] + df['spread']*df['I']*(df['I']**2+1)/4
df['adjust_mid_price_3'] = df['mid_price'] + df['spread']*df['I']**3/2
df['adjust_mid_price_4'] = df['mid_price'] + df['spread']*(df['I']+0.3)*(df['I']**4+0.7)/3.8

print('平均值     mid_price的误差：', ((df['price']-df['mid_price'])**2).sum())
print('挂单量加权 mid_price的误差：', ((df['price']-df['weight_mid_price'])**2).sum())
print('调整后的   mid_price的误差：', ((df['price']-df['adjust_mid_price'])**2).sum())
print('调整后的 mid_price_2的误差：', ((df['price']-df['adjust_mid_price_2'])**2).sum())
print('调整后的 mid_price_3的误差：', ((df['price']-df['adjust_mid_price_3'])**2).sum())
print('调整后的 mid_price_4的误差：', ((df['price']-df['adjust_mid_price_4'])**2).sum())

平均值     mid_price的误差： 0.0048751924999999845
挂单量加权 mid_price的误差： 0.0048373440193987035
调整后的   mid_price的误差： 0.004803654771638586
调整后的 mid_price_2的误差： 0.004808216498329721
调整后的 mid_price_3的误差： 0.004794984755260528
调整后的 mid_price_4的误差： 0.0047909595497071375

دوسرے گیئر کی گہرائی پر غور کریں۔

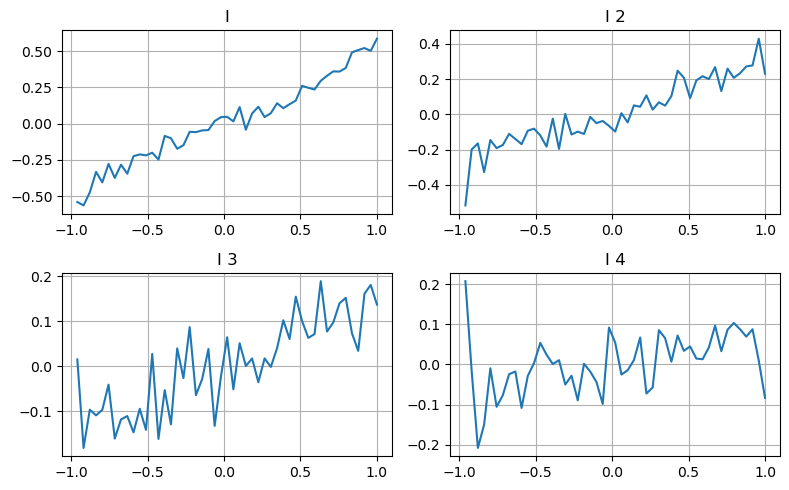
یہاں ہم پچھلے مضمون کے خیال کا استعمال کرتے ہوئے ایک خاص اثر انداز پیرامیٹر کی مختلف ویلیو رینجز اور لین دین کی قیمت میں تبدیلیوں کو جانچنے کے لیے استعمال کرتے ہیں تاکہ اس پیرامیٹر کے درمیانی قیمت میں شراکت کی پیمائش کی جا سکے۔ جیسا کہ پہلے درجے کے گہرائی کے گراف میں دکھایا گیا ہے، جیسے جیسے میں بڑھتا ہوں، اگلی لین دین کی قیمت میں مثبت تبدیلی کا امکان زیادہ ہوتا ہے، جس کا مطلب ہے کہ میں مثبت شراکت کرتا ہوں۔

دوسری کھیپ پر بھی اسی طرح عمل کیا گیا، اور یہ معلوم ہوا کہ اگرچہ اثر پہلے بیچ سے تھوڑا چھوٹا تھا، لیکن پھر بھی یہ نہ ہونے کے برابر تھا۔ گہرائی کا تیسرا درجہ بھی تھوڑا سا حصہ ڈالتا ہے، لیکن یکجہتی بہت زیادہ خراب ہے، اور گہرائی کی گہرائی بنیادی طور پر کوئی حوالہ قیمت نہیں رکھتی ہے۔

مختلف شراکت کی سطحوں کے مطابق، تین سطحوں کے عدم توازن کے پیرامیٹرز کے لیے مختلف وزن تفویض کیے گئے ہیں، اصل معائنہ سے پتہ چلتا ہے کہ حساب کے مختلف طریقوں کے لیے پیشین گوئی کی غلطیاں مزید کم ہو گئی ہیں۔

bins = np.linspace(-1, 1, 50)
df['change'] = (df['price'].pct_change().shift(-1))/tick_size
df['I_bins'] = pd.cut(df['I'], bins, labels=bins[1:])
df['I_2'] = (df['bid_1_quantity'] - df['ask_1_quantity']) / (df['bid_1_quantity'] + df['ask_1_quantity'])
df['I_2_bins'] = pd.cut(df['I_2'], bins, labels=bins[1:])
df['I_3'] = (df['bid_2_quantity'] - df['ask_2_quantity']) / (df['bid_2_quantity'] + df['ask_2_quantity'])
df['I_3_bins'] = pd.cut(df['I_3'], bins, labels=bins[1:])
df['I_4'] = (df['bid_3_quantity'] - df['ask_3_quantity']) / (df['bid_3_quantity'] + df['ask_3_quantity'])
df['I_4_bins'] = pd.cut(df['I_4'], bins, labels=bins[1:])
fig, axes = plt.subplots(nrows=2, ncols=2, figsize=(8, 5))


axes[0][0].plot(df.groupby('I_bins')['change'].mean())
axes[0][0].set_title('I')
axes[0][0].grid(True)

axes[0][1].plot(df.groupby('I_2_bins')['change'].mean())
axes[0][1].set_title('I 2')
axes[0][1].grid(True)

axes[1][0].plot(df.groupby('I_3_bins')['change'].mean())
axes[1][0].set_title('I 3')
axes[1][0].grid(True)

axes[1][1].plot(df.groupby('I_4_bins')['change'].mean())
axes[1][1].set_title('I 4')
axes[1][1].grid(True)
plt.tight_layout();

df['adjust_mid_price_4'] = df['mid_price'] + df['spread']*(df['I']+0.3)*(df['I']**4+0.7)/3.8
df['adjust_mid_price_5'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2'])/2
df['adjust_mid_price_6'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2'])**3/2
df['adjust_mid_price_7'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.3*df['I_2']+0.3)*((0.7*df['I']+0.3*df['I_2'])**4+0.7)/3.8
df['adjust_mid_price_8'] = df['mid_price'] + df['spread']*(0.7*df['I']+0.2*df['I_2']+0.1*df['I_3']+0.3)*((0.7*df['I']+0.3*df['I_2']+0.1*df['I_3'])**4+0.7)/3.8

print('调整后的 mid_price_4的误差：', ((df['price']-df['adjust_mid_price_4'])**2).sum())
print('调整后的 mid_price_5的误差：', ((df['price']-df['adjust_mid_price_5'])**2).sum())
print('调整后的 mid_price_6的误差：', ((df['price']-df['adjust_mid_price_6'])**2).sum())
print('调整后的 mid_price_7的误差：', ((df['price']-df['adjust_mid_price_7'])**2).sum())
print('调整后的 mid_price_8的误差：', ((df['price']-df['adjust_mid_price_8'])**2).sum())

调整后的 mid_price_4的误差： 0.0047909595497071375
调整后的 mid_price_5的误差： 0.0047884350488318714
调整后的 mid_price_6的误差： 0.0047778319053133735
调整后的 mid_price_7的误差： 0.004773578540592192
调整后的 mid_price_8的误差： 0.004771415189297518

لین دین کے اعداد و شمار پر غور کریں۔

لین دین کا ڈیٹا براہ راست طویل اور مختصر پوزیشنوں کی ڈگری کی عکاسی کرتا ہے، یہ ایک ایسا آپشن ہے جس میں حقیقی رقم شامل ہوتی ہے، اور آرڈر دینے کی لاگت بہت کم ہوتی ہے، اور یہاں تک کہ جان بوجھ کر آرڈر پلیسمنٹ کی دھوکہ دہی کے واقعات بھی ہوتے ہیں۔ لہذا، درمیانی قیمت کی پیشن گوئی کرتے وقت، حکمت عملی کو لین دین کے ڈیٹا پر توجہ دینی چاہیے۔

فارم پر غور کرتے ہوئے، آرڈر کی اوسط آمد کی مقدار کے عدم توازن کی وضاحت کریں VI, Vb, Vs بالترتیب خرید آرڈرز اور سیل آرڈرز فی یونٹ ایونٹ کی اوسط مقدار کی نمائندگی کرتے ہیں۔

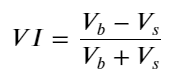
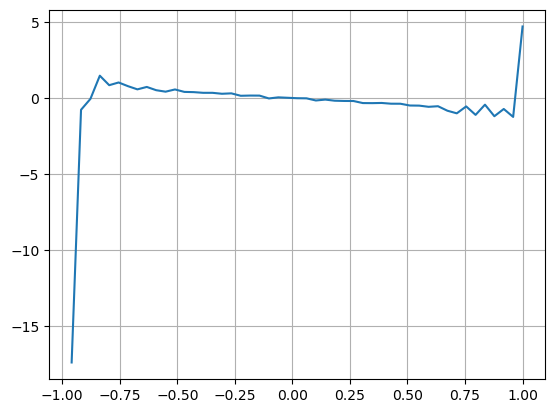
نتائج سے پتہ چلتا ہے کہ قیمت میں تبدیلی کی پیشن گوئی کرنے میں مختصر مدت میں آمد کی مقدار سب سے زیادہ اہم ہوتی ہے جب VI (0.1-0.9) کے درمیان ہوتا ہے، یہ قیمت کے ساتھ منفی طور پر منسلک ہوتا ہے، لیکن حد سے باہر اس کا مثبت تعلق ہوتا ہے۔ قیمت اس سے پتہ چلتا ہے کہ جب مارکیٹ حد سے زیادہ نہیں ہوتی ہے، تو یہ بنیادی طور پر اتار چڑھاؤ کی طرف متوجہ ہوتا ہے اور جب مارکیٹ کے انتہائی حالات ہوتے ہیں، جیسے کہ بڑی تعداد میں خرید کے آرڈرز زیادہ فروخت ہوتے ہیں، تو رجحان رجحان سے باہر ہو جائے گا۔ . یہاں تک کہ اگر ہم ان کم امکانی حالات کو نظر انداز کر دیں اور صرف یہ مان لیں کہ رجحان اور VI ایک منفی لکیری تعلق کو پورا کرتے ہیں، درمیانی قیمت کی پیشین گوئی کی غلطی بہت کم ہو جاتی ہے۔ فارمولے میں a عدد کو ظاہر کرتا ہے۔

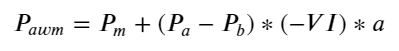
alpha=0.1

df['avg_buy_interval'] = None
df['avg_sell_interval'] = None
df.loc[df['is_buyer_maker'] == True, 'avg_buy_interval'] = df[df['is_buyer_maker'] == True]['transact_time'].diff().ewm(alpha=alpha).mean()
df.loc[df['is_buyer_maker'] == False, 'avg_sell_interval'] = df[df['is_buyer_maker'] == False]['transact_time'].diff().ewm(alpha=alpha).mean()

df['avg_buy_quantity'] = None
df['avg_sell_quantity'] = None
df.loc[df['is_buyer_maker'] == True, 'avg_buy_quantity'] = df[df['is_buyer_maker'] == True]['quantity'].ewm(alpha=alpha).mean()
df.loc[df['is_buyer_maker'] == False, 'avg_sell_quantity'] = df[df['is_buyer_maker'] == False]['quantity'].ewm(alpha=alpha).mean()

df['avg_buy_quantity'] = df['avg_buy_quantity'].fillna(method='ffill')
df['avg_sell_quantity'] = df['avg_sell_quantity'].fillna(method='ffill')
df['avg_buy_interval'] = df['avg_buy_interval'].fillna(method='ffill')
df['avg_sell_interval'] = df['avg_sell_interval'].fillna(method='ffill')

df['avg_buy_rate'] = 1000 / df['avg_buy_interval']
df['avg_sell_rate'] =1000 / df['avg_sell_interval']

df['avg_buy_volume'] = df['avg_buy_rate']*df['avg_buy_quantity']
df['avg_sell_volume'] = df['avg_sell_rate']*df['avg_sell_quantity']

df['I'] = (df['bid_0_quantity']- df['ask_0_quantity']) / (df['bid_0_quantity'] + df['ask_0_quantity'])
df['OI'] = (df['avg_buy_rate']-df['avg_sell_rate']) / (df['avg_buy_rate'] + df['avg_sell_rate'])
df['QI'] = (df['avg_buy_quantity']-df['avg_sell_quantity']) / (df['avg_buy_quantity'] + df['avg_sell_quantity'])
df['VI'] = (df['avg_buy_volume']-df['avg_sell_volume']) / (df['avg_buy_volume'] + df['avg_sell_volume'])

bins = np.linspace(-1, 1, 50)
df['VI_bins'] = pd.cut(df['VI'], bins, labels=bins[1:])
plt.plot(df.groupby('VI_bins')['change'].mean());
plt.grid(True)

df['adjust_mid_price'] = df['mid_price'] + df['spread']*df['I']/2
df['adjust_mid_price_9'] = df['mid_price'] + df['spread']*(-df['OI'])*2
df['adjust_mid_price_10'] = df['mid_price'] + df['spread']*(-df['VI'])*1.4

print('调整后的mid_price   的误差：', ((df['price']-df['adjust_mid_price'])**2).sum())
print('调整后的mid_price_9 的误差：', ((df['price']-df['adjust_mid_price_9'])**2).sum())
print('调整后的mid_price_10的误差：', ((df['price']-df['adjust_mid_price_10'])**2).sum())

调整后的mid_price   的误差： 0.0048373440193987035
调整后的mid_price_9 的误差： 0.004629586542840461
调整后的mid_price_10的误差： 0.004401790287167206

جامع درمیانی قیمت

اس بات کو مدنظر رکھتے ہوئے کہ زیر التواء آرڈرز اور ٹرانزیکشن ڈیٹا دونوں درمیانی قیمت کی پیشن گوئی کے لیے مددگار ہیں، ان دونوں پیرامیٹرز کو ملایا جا سکتا ہے یہاں وزن کی تفویض صوابدیدی ہے اور انتہائی صورتوں میں، پیش گوئی کی گئی درمیانی قیمت نہیں ہو سکتی ایک خریدنے اور ایک بیچنے کے درمیان، لیکن جب تک غلطی کو کم کیا جا سکتا ہے، ان تفصیلات سے کوئی فرق نہیں پڑتا ہے۔

آخر میں، پیشین گوئی کی غلطی ابتدائی 0.00487 سے کم ہو گئی ہے، ہم ابھی بھی درمیانی قیمت کے بارے میں بہت کچھ نہیں سوچیں گے۔ .

#注意VI需要延后一个使用
df['price_change'] = np.log(df['price']/df['price'].rolling(40).mean())
df['CI'] = -1.5*df['VI'].shift()+0.7*(0.7*df['I']+0.2*df['I_2']+0.1*df['I_3'])**3 + 150*df['price_change'].shift(1)

df['adjust_mid_price_11'] = df['mid_price'] + df['spread']*(df['CI'])
print('调整后的mid_price_11的误差：', ((df['price']-df['adjust_mid_price_11'])**2).sum())

调整后的mid_price_11的误差： 0.00421125960463469

خلاصہ کریں۔

یہ کاغذ درمیانی قیمت کے حساب کتاب کے طریقہ کار کو مزید بہتر بنانے کے لیے گہرائی کے اعداد و شمار اور لین دین کے اعداد و شمار کو یکجا کرتا ہے اور قیمت کی تبدیلیوں کی پیشن گوئی کی درستگی کو بہتر بنانے کا طریقہ فراہم کرتا ہے۔ مجموعی طور پر، مختلف پیرامیٹرز بہت سخت نہیں ہیں اور صرف حوالہ کے لیے ہیں۔ زیادہ درست درمیانی قیمت کے ساتھ، اگلا مرحلہ اصل میں بیک ٹیسٹنگ کے لیے درمیانی قیمت کو لاگو کرنا ہے، اس لیے ہم کچھ دیر کے لیے اپ ڈیٹ کرنا بند کر دیں گے۔