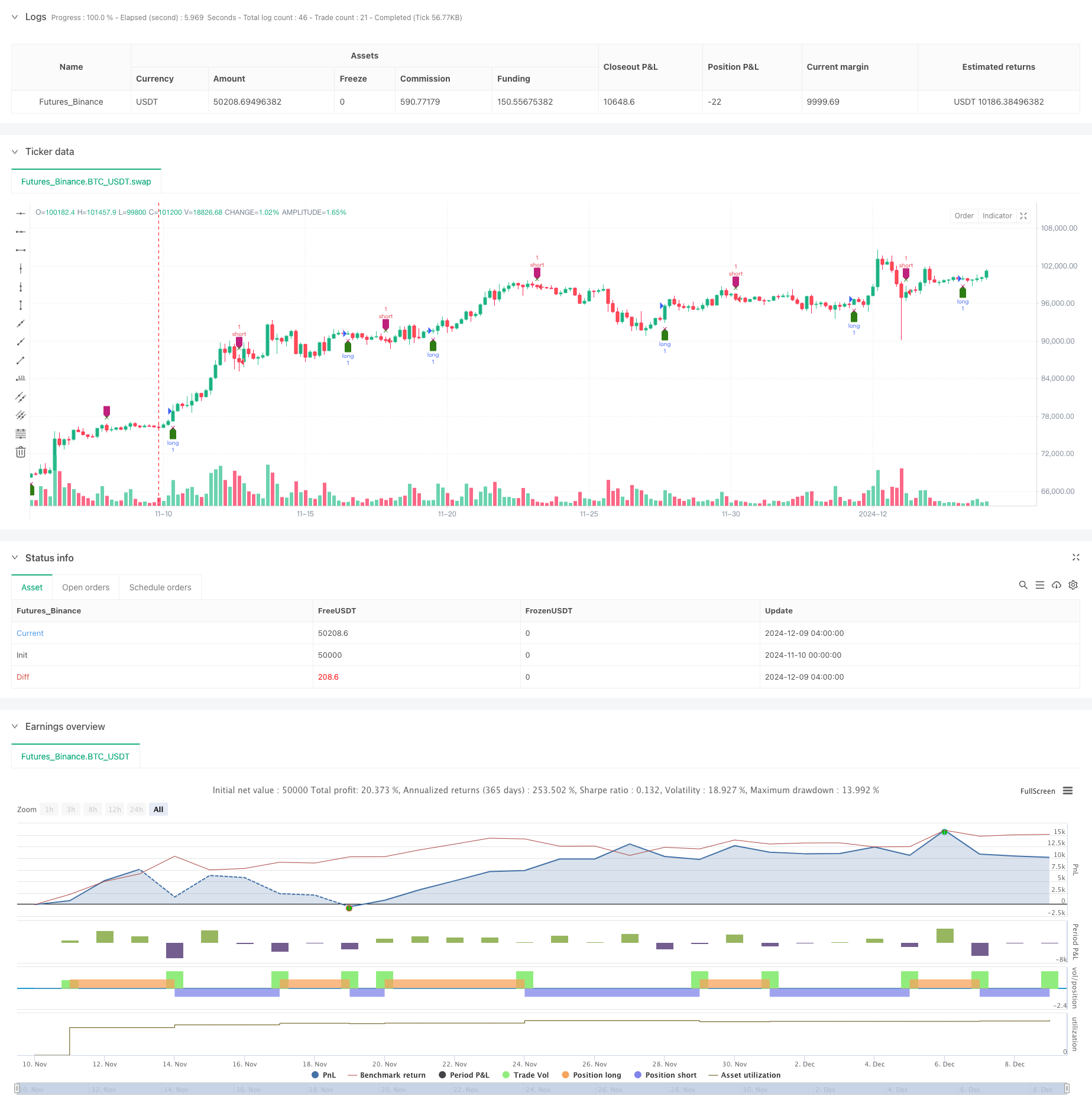
یہ حکمت عملی آر ایس آئی کے متحرک oscillators پر مبنی ایک مقداری تجارتی نظام ہے۔ آر ایس آئی اشارے پر کثیر مقصود اور وقت کی ترتیب کا تجزیہ کرکے ، آر ایس آئی میں تبدیلی کی شرح کا حساب کتاب کرکے مارکیٹ کی حرکیات کو پکڑنے کے لئے۔ حکمت عملی اعلی ریاضی کے طریقوں جیسے سگنل پروسیسنگ جیسے کیو آر ڈس انکولیشن کا استعمال کرتی ہے ، اور تجارت کے فیصلوں کے لئے یکساں لکیری نظام کے ساتھ مل کر۔
حکمت عملی کا اصول
اس حکمت عملی کا مرکز ڈیلٹا-آر ایس آئی آسکیلیٹر ہے ، جو مندرجہ ذیل اقدامات کے ذریعے حاصل کیا جاتا ہے:
- سب سے پہلے، روایتی RSI کے اعداد و شمار کے طور پر بنیادی اعداد و شمار کا حساب لگائیں.
- RSI کو ہموار کرنے اور شور کو کم کرنے کے لئے کثیر مقصود فٹ کا استعمال کریں
- RSI کے ٹائم کوڈینٹیول کو ڈیلٹا-RSI سے حاصل کیا جاتا ہے جو RSI کی تبدیلی کی شرح کو ظاہر کرتا ہے
- ڈیلٹا-آر ایس آئی کا موازنہ اس کی حرکت پذیری اوسط کے ساتھ ٹریڈنگ سگنل تیار کرتا ہے
- مساوی جڑ کی غلطی ((RMSE) کا استعمال کرتے ہوئے فٹنس کے معیار کا اندازہ اور فلٹرنگ
ٹرانزیکشن سگنل تین طریقوں سے پیدا ہوتے ہیں:
- صفر لائن کراسنگ: ڈیلٹا-آر ایس آئی منفی سے درست ہونے پر زیادہ ہے ، مثبت سے منفی ہونے پر خالی ہے
- سگنل لائن کراسنگ: ڈیلٹا-آر ایس آئی کو اس کی چلتی اوسط سے اوپر / نیچے جانے پر زیادہ / کم کرنا
- سمت میں تبدیلی: ڈیلٹا-آر ایس آئی نے منفی علاقوں میں اضافے کا آغاز کیا اور مثبت علاقوں میں کمی کا آغاز کیا
اسٹریٹجک فوائد
- ریاضی کی مضبوط بنیاد: سگنل پروسیسنگ کے لئے اعلی درجے کی ریاضی کے طریقوں جیسے QR تجزیہ کا استعمال کرتے ہوئے ، نظریاتی بنیاد قابل اعتماد ہے
- سگنل ہموار: ملٹی میٹم کو مؤثر طریقے سے مارکیٹ کے شور کو فلٹر کرنے اور سگنل کے معیار کو بہتر بنانے کے لئے
- لچکدار: مختلف مارکیٹ کے حالات کے مطابق سگنل جنریشن کے مختلف طریقوں اور پیرامیٹرز کے انتخاب کی پیش کش
- خطرے کو کنٹرول کیا جاسکتا ہے: آر ایم ایس ای فلٹرنگ میکانزم پر مشتمل ہے ، جو اعلی وشوسنییتا سگنل کو فلٹر کرتا ہے
- اعلی کمپیوٹنگ کارکردگی: میٹرکس آپریشنز بہتر الگورتھم استعمال کرتے ہیں ، جو اعلی کارکردگی کا مظاہرہ کرتے ہیں
اسٹریٹجک رسک
- پیرامیٹر حساس: متعدد کلیدی پیرامیٹرز کو احتیاط سے ایڈجسٹ کرنے کی ضرورت ہے ، اور پیرامیٹرز کا غلط انتخاب حکمت عملی کی کارکردگی کو شدید متاثر کرسکتا ہے
- تاخیر: سگنل کی ہموار پروسیسنگ کچھ تاخیر کا باعث بنتی ہے ، جس سے تیز رفتار کو یاد کیا جاسکتا ہے
- جعلی بریک: ہلچل مچانے والی مارکیٹوں میں جعلی سگنل پیدا کرنے اور ٹرانزیکشن کی لاگت میں اضافے کا خطرہ
- پیچیدہ حساب کتاب: زیادہ میٹرکس آپریشنز میں ملوث ، اعلی تعدد تجارت میں ممکنہ کارکردگی کا مسئلہ
- اوور فٹ: پیرامیٹرز کو بہتر بنانے کے لئے احتیاط کی ضرورت ہے کہ تاریخ کے اعداد و شمار کو زیادہ سے زیادہ فٹ نہ کیا جائے
حکمت عملی کی اصلاح کی سمت
- ایڈجسٹمنٹ پیرامیٹرز: مارکیٹ میں اتار چڑھاؤ کی رفتار کے مطابق آر ایس آئی کے دورانیے اور فٹ ہونے والے مرحلے کو ایڈجسٹ کیا جاسکتا ہے
- کثیر ٹائم سائیکل: زیادہ ٹائم سائیکل کے ساتھ مل کر سگنل کو کراس کی توثیق کریں
- اتار چڑھاؤ کی شرح فلٹرنگ: ATR جیسے اتار چڑھاؤ کی شرح کے اشارے شامل کرنے کے لئے سگنل فلٹرنگ
- مارکیٹ کی درجہ بندی: مارکیٹ کی مختلف حالتوں کے لئے مختلف سگنل جنریشن قواعد کا استعمال کرتے ہوئے ((رجحان / ہلچل)
- اسٹاپ نقصان کی اصلاح: مزید ذہین اسٹاپ نقصان کے طریقہ کار کو شامل کرنا ، جیسے مزاحمت کی حمایت پر مبنی متحرک اسٹاپ نقصان
خلاصہ کریں۔
یہ ایک اچھی طرح سے تشکیل شدہ ، مضبوط نظریاتی بنیادوں والی ایک مقداری تجارت کی حکمت عملی ہے۔ آر ایس آئی کی متحرک خصوصیات کے تجزیہ کے ذریعہ ، جدید ریاضی کے طریقوں کے ساتھ مل کر سگنل پروسیسنگ کے ذریعہ ، مارکیٹ کے رجحانات کو بہتر طور پر پکڑنے کے قابل ہے۔ اگرچہ کچھ پیرامیٹرز کی حساسیت اور حساب کتاب کی پیچیدگی کے مسائل موجود ہیں ، لیکن معقول پیرامیٹرز کے انتخاب اور اصلاحی بہتری کے ذریعہ ، اس حکمت عملی میں اچھی اطلاق کی قیمت ہے۔ یہ مشورہ دیا جاتا ہے کہ خطرے پر قابو پانے ، معقول پوزیشنوں کی ترتیب اور حکمت عملی کی کارکردگی کی مستقل نگرانی پر توجہ دی جائے۔
/*backtest
start: 2024-11-10 00:00:00
end: 2024-12-09 08:00:00
period: 4h
basePeriod: 4h
exchanges: [{"eid":"Futures_Binance","currency":"BTC_USDT"}]
*/
// This source code is subject to the terms of the Mozilla Public License 2.0 at https://mozilla.org/MPL/2.0/
// © tbiktag
//
// Delta-RSI Oscillator Strategy- 1