روایتی تکنیکی تجزیہ پیچیدہ مارکیٹوں میں کیوں ناکام ہے؟

کوانٹم ٹریڈنگ کے شعبے میں ، ہم اکثر اس طرح کی الجھن میں پڑ جاتے ہیں: کیوں سادہ منتقل اوسط یا آر ایس آئی پر مبنی حکمت عملی کچھ مارکیٹ کے حالات میں عمدہ کارکردگی کا مظاہرہ کرتی ہے ، اور دوسری مدت میں بار بار ناکام ہوجاتی ہے؟ اس کا جواب مالیاتی ٹائم سیریز کی پیچیدگی میں ہے۔

آج کی حکمت عملی ، جس میں آر آر ((2) خود سے رجوع کرنے والے ماڈل اور گارچ ((1) مشروط تغیراتی ماڈل کا ایک ہوشیار امتزاج ہے ، اس مسئلے کو اعدادوشمار کے نقطہ نظر سے حل کرنے کی کوشش کرتی ہے۔ یہ محض تکنیکی اشارے کی چڑھائی نہیں ہے ، بلکہ مالی ٹائم سیریز کی بنیادی خصوصیات کی گہرائی میں کھدائی ہے۔

اے آر: 2) ماڈل قیمتوں کے میموری اثر کو کیسے پکڑتا ہے؟

حکمت عملی کا مرکز AR ((2) خود سے واپسی کے ماڈل کا اطلاق ہے۔ خود سے واپسی کیا ہے؟ آسان الفاظ میں ، ماضی کی خود کو مستقبل کی خود کی پیش گوئی کرنے کے لئے استعمال کرنا ہے۔ AR ((2) ماڈل فرض کرتا ہے کہ موجودہ منافع کی شرح کو پہلے دو ادوار کی شرح منافع سے لکیری طور پر ظاہر کیا جاسکتا ہے:

            
            
            
r_t = φ₁ × r_{t-1} + φ₂ × r_{t-2} + ε_t

کوڈ میں یول-والکر مساوات کے ذریعے کوفیشنرφ1 اورφ2 کو حل کریں:

            pinescript
            
            
c0 = calcAutoCovariance(returns, 0, lengthReg) // 滞后0期自协方差
c1 = calcAutoCovariance(returns, 1, lengthReg) // 滞后1期自协方差  
c2 = calcAutoCovariance(returns, 2, lengthReg) // 滞后2期自协方差
phi1 = (c1 * c0 - c2 * c1) / denominator // 第一个自回归系数
phi2 = (c2 * c0 - c1 * c1) / denominator // 第二个自回归系数

اس طریقہ کار کا فائدہ یہ ہے کہ اس کا انحصار کسی بھی طرح کے فیصلے پر نہیں ہوتا۔ اس کے بجائے ، یہ اعداد و شمار کو خود "بات کرنے" دیتا ہے اور قیمتوں کی ترتیب میں مضمر باقاعدگی کو دریافت کرتا ہے۔

GARCH ماڈل مارکیٹ کے خطرے کو بہتر طریقے سے کیسے پیش کرتا ہے؟

صرف اے آر ماڈل کافی نہیں ہے ، کیونکہ مالیاتی منڈیوں میں اتار چڑھاؤ کی شرح مستقل نہیں ہے۔ ہم سب جانتے ہیں کہ "تباؤ کی شرح جمع" کے رجحان میں بڑے پیمانے پر اتار چڑھاؤ اکثر بڑے پیمانے پر اتار چڑھاؤ کے ساتھ ہوتا ہے ، اور خاموشی زیادہ دیر تک جاری رہتی ہے۔

GARCH ((1,1) ماڈل اس خصوصیت کو ظاہر کرنے کے لئے بنایا گیا ہے:

            
            
            
σ²_t = ω + α × ε²_{t-1} + β × σ²_{t-1}

کوڈ میں لاگو ہونے والی منطق اس بات کو واضح طور پر ظاہر کرتی ہے:

            pinescript
            
            
omega = (1 - adjustedAlpha - adjustedBeta) * longTermVar
garchVariance := omega + adjustedAlpha * math.pow(arResidual[1], 2) + adjustedBeta * garchVariance[1]

یہاں ایک اہم بصیرت یہ ہے کہ: موجودہ کنڈیشنری تقریباً پچھلے دور کے بقایا کے مربع پر منحصر ہے ((قلیل مدتی جھٹکے) ، بلکہ پچھلے دور کے کنڈیشنری کے فرق پر بھی انحصار کرتا ہے ((طویل مدتی تسلسل)) ۔ پیرامیٹر α قلیل مدتی جھٹکے کے اثرات کو کنٹرول کرتا ہے ، اور β اتار چڑھاؤ کی شرح کی تسلسل کو کنٹرول کرتا ہے۔

حکمت عملی کی تجارت کی منطق کس طرح خطرے اور فوائد کو متوازن کرتی ہے؟

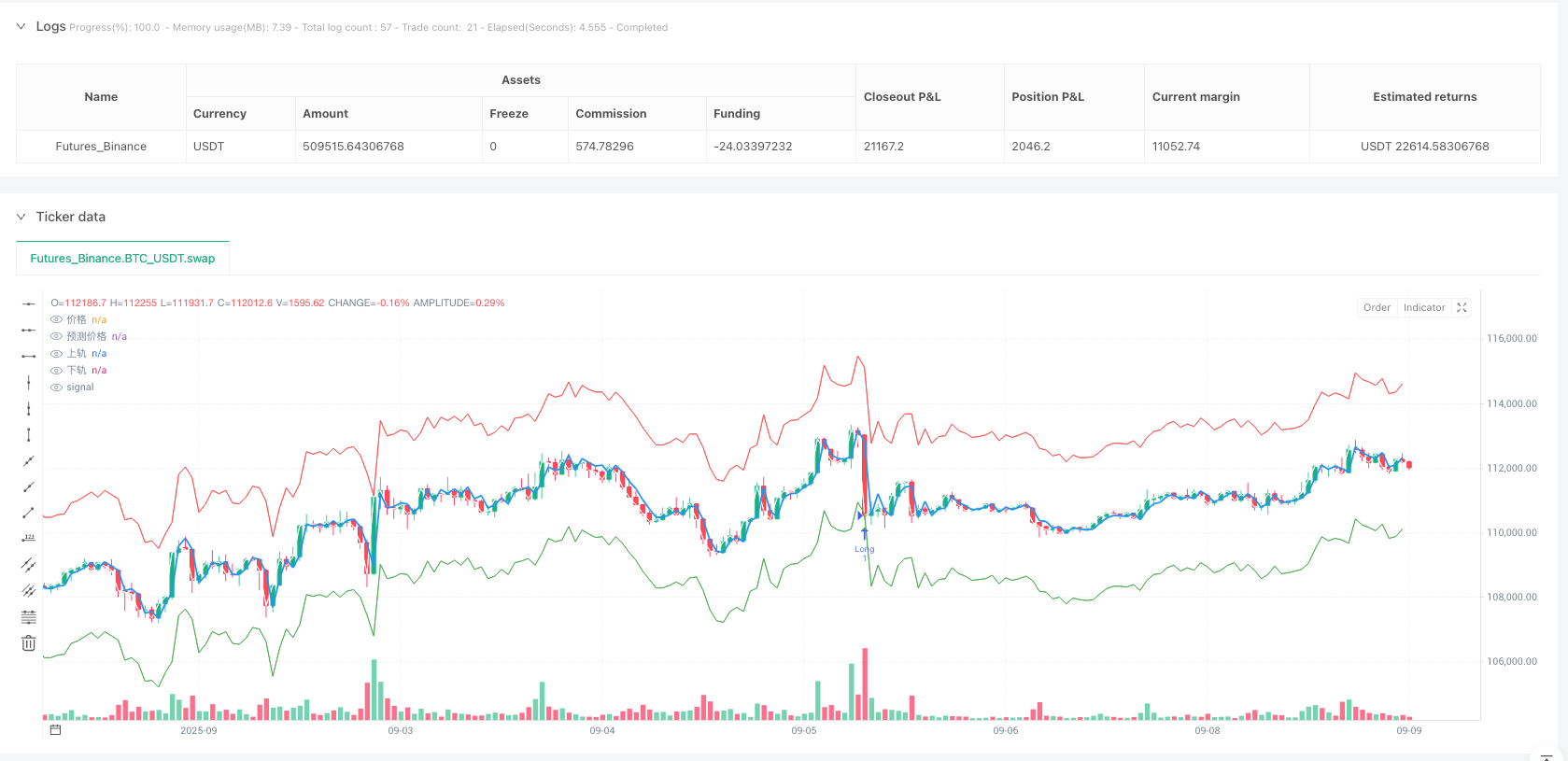
اے آر کی پیش گوئی اور گارچ کے اتار چڑھاؤ کی شرح کے تخمینے کے ساتھ ، حکمت عملی نے اعتماد کی ایک متحرک حد تشکیل دی:

            pinescript
            
            
upperReturnBand = arReturnPredict + stdevFactor * garchStd
lowerReturnBand = arReturnPredict - stdevFactor * garchStd

ٹرانزیکشن سگنل کی پیداوار کا منطق اوسط ریٹرنشن کے خیال کو ظاہر کرتا ہے:

• جب قیمت نیچے کی طرف گرتی ہے تو زیادہ کام کریں
• جب قیمت ٹریک سے باہر نکل جاتی ہے تو خالی ہوجاتا ہے

اس طرح کے ڈیزائن کی چال یہ ہے کہ: اعتماد کی حد کی چوڑائی مارکیٹ کی اتار چڑھاؤ کی شرح کے مطابق متحرک طور پر ایڈجسٹ ہوتی ہے۔ اعلی اتار چڑھاؤ کے دوران ، حد وسیع ہوجاتی ہے ، جس سے تجارت کی فریکوئنسی کم ہوجاتی ہے۔ کم اتار چڑھاؤ کے دوران ، حد تنگ ہوجاتی ہے ، جس سے تجارت کے مواقع بڑھ جاتے ہیں۔

کیا آپ کے خیال میں اس کے عملی استعمال میں کن اہم مسائل پر توجہ دینے کی ضرورت ہے؟

ماڈل استحکام ٹیسٹ
کوڈ میں اہم استحکام کی جانچ پڑتال شامل ہے:

            pinescript
            
            
if stabilityCheck >= 0.99 or math.abs(phi2) >= 0.99
    scaleFactor = 0.95 / math.max(stabilityCheck, math.abs(phi2) + 0.01)

اس سے اے آر ماڈل کی مستقل مزاجی کو یقینی بنایا جاتا ہے ، جس سے متفرق پیش گوئی کے نتائج سے بچا جاتا ہے۔

2. پیرامیٹرز کے قریب ہونے کی پابندی
GARCH ماڈل نے طویل مدتی فرق کے وجود کو یقینی بنانے کے لئے α + β < 1 کا مطالبہ کیا:

            pinescript
            
            
if sumParam >= 0.999
    scale = 0.99 / sumParam

3 فلٹرنگ میکانزم کی ضرورت
حکمت عملی آر ایس آئی فلٹرنگ کے اختیارات پیش کرتی ہے ، جو عملی استعمال میں اہم ہے۔ خالص اعدادوشمار کے ماڈل مارکیٹ کی رجحان سازی کی خصوصیات کو نظرانداز کرسکتے ہیں ، اور تکنیکی اشارے شامل کرنے سے اضافی تصدیق کے اشارے مل سکتے ہیں۔

حکمت عملی کی حدود اور اصلاحات

اگرچہ یہ حکمت عملی نظریاتی طور پر خوبصورت ہے ، لیکن عملی طور پر اس پر غور کرنے کی ضرورت ہے:

ڈیٹا فریکوئنسی کا انتخاب:AR-GARCH ماڈل مختلف ادوار کے تحت کارکردگی میں بہت زیادہ فرق کرتا ہے۔ ہائی فریکوئنسی ڈیٹا زیادہ معلومات فراہم کرتا ہے ، لیکن اس میں زیادہ شور بھی شامل ہے۔

پیرامیٹرز کی تبدیلی: موجودہ عمل میں فرض کیا گیا ہے کہ AR اور GARCH پیرامیٹرز تخمینہ ونڈو کے اندر مستقل ہیں ، لیکن مارکیٹ کی اصل ساخت میں تبدیلی آسکتی ہے۔

ٹرانزیکشن لاگت کا اثراعداد و شمار کے مطابق ، اسٹریٹجک ارورائزنگ کی حکمت عملی میں عام طور پر اعلی تجارتی تعدد کی ضرورت ہوتی ہے ، اور اس کی فیس اور سلائڈ پوائنٹ لاگت کو نظرانداز نہیں کیا جاسکتا ہے۔

خلاصہ: اعدادوشمار کے ماڈلنگ کی قدر

یہ AR-GARCH حکمت عملی مالیاتی ماڈلنگ میں جدید اعدادوشمار کی طاقت کو ظاہر کرتی ہے۔ یہ تکنیکی اشارے کا ایک سادہ مجموعہ نہیں ہے ، بلکہ مالیاتی ٹائم سیریز کے اعدادوشمار کی خصوصیات کی گہرائی میں کھدائی ہے۔

کوانٹم ٹریڈرز کے لئے ، اس طرح کی حکمت عملیوں کو سمجھنے کی قدر نہ صرف براہ راست اطلاق میں ہے ، بلکہ اعدادوشمار کے ذہن میں مارکیٹوں کا تجزیہ کرنے کی صلاحیت میں ہے۔ آج ، جب AI اور مشین لرننگ کا رجحان ہے ، تو یہ کلاسک شماریاتی ماڈل مارکیٹوں کو سمجھنے اور حکمت عملی تیار کرنے کے لئے ایک اہم بنیاد ہیں۔