Hãy cùng thảo luận về cách tối ưu hóa các tham số của một số mô hình giao dịch theo chương trình

• #### Cao nguyên tham số và đảo cô lập tham số

　 Một nguyên tắc quan trọng trong tối ưu hóa tham số là phải tranh giành các tham số cao hơn là các tham số cô lập. Các tham số cao có nghĩa là có một phạm vi tham số rộng hơn, mô hình có thể đạt được hiệu quả tốt hơn trong phạm vi tham số này, thường sẽ hình thành một phân bố gần như chính xác với trung tâm của cao. Các tham số cô lập có nghĩa là mô hình chỉ có hiệu suất tốt khi giá trị tham số nằm trong một phạm vi rất nhỏ, và khi tham số lệch khỏi giá trị đó, hiệu suất của mô hình sẽ thay đổi đáng kể.

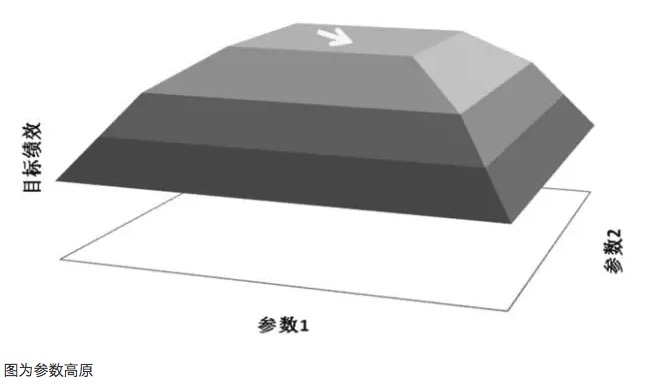
• #### Hình ảnh là các tham số cao nguyên

Lấy biểu đồ cao nguyên tham số và biểu đồ đảo tham số làm ví dụ, giả sử một mô hình giao dịch có hai tham số, lần lượt là tham số 1 và tham số 2, sau khi thử nghiệm hai tham số, sẽ có một biểu đồ hiệu suất ba chiều. Phân bố tham số tốt nên là biểu đồ cao nguyên tham số, ngay cả khi thiết lập các tham số bị lệch, hiệu suất lợi nhuận của mô hình vẫn có thể được đảm bảo.

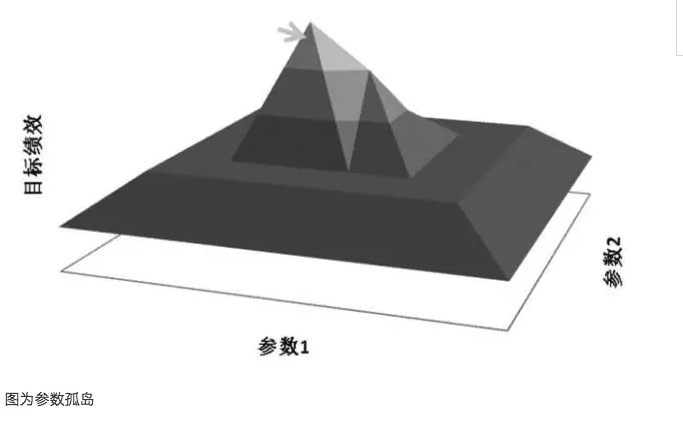
Nói chung, nếu hệ thống tham số gần đó có hiệu suất kém hơn nhiều so với tham số tối ưu, thì tham số tối ưu có thể là kết quả của sự tổng hợp quá mức, có thể được coi là giải pháp điểm kỳ lạ, chứ không phải là giải pháp giá trị cực lớn cần tìm. Từ góc độ toán học, điểm kỳ lạ là không ổn định, trong tình huống không chắc chắn trong tương lai, tham số tối ưu có thể trở thành tham số tối thiểu một khi đặc điểm thị trường thay đổi.

Sự phù hợp quá mức có liên quan đến mẫu được chọn, nếu mẫu được chọn không đại diện cho đặc điểm tổng thể của thị trường và chỉ điều chỉnh tham số để kết quả thử nghiệm đạt được giá trị mong đợi tích cực, thì điều này chắc chắn là tự lừa dối, và giá trị tham số thu được là giá trị tham số không hiệu quả của sự phù hợp quá mức. Ví dụ, bằng cách phân tích tham số phù hợp quá mức, mô hình giao dịch có hiện tượng tăng lợi nhuận ở các giá trị 35 và 63, tương ứng, nếu chỉ số tương ứng trong mô hình được chọn làm tham số 35 và 63, lợi nhuận của mô hình có vẻ hoàn hảo, nhưng thực tế là hiệu ứng đảo cô lập của tham số điển hình.

Sự mâu thuẫn chính giữa quá phù hợp và tối ưu hóa tham số là các tham số tối ưu được tối ưu hóa tham số mô hình chỉ dựa trên mẫu dữ liệu lịch sử đã xảy ra, trong khi hành động trong tương lai là thay đổi động, có cả tương tự và biến đổi so với hành động trong lịch sử. Các nhà thiết kế mô hình có thể tìm thấy tham số mô hình có hiệu suất tốt nhất trong lịch sử, nhưng tham số này không nhất thiết phải là tốt nhất trong ứng dụng thực tế của mô hình trong tương lai, thậm chí là tham số mô hình có hiệu suất tốt nhất trong lịch sử, có thể là tham số có hiệu suất rất tệ trong mô hình thực tế trong tương lai, thậm chí mang lại tổn thất lớn. Ví dụ, chọn một tham số có thể nắm bắt một làn sóng lớn trong lịch sử, nhưng thiết lập một mô hình với giá trị tham số như vậy không có nghĩa là mô hình có thể hoạt động tốt trong cuộc chiến trong tương lai, và tham số lịch sử tốt hơn có thể không giúp gì trong mô hình trong tương lai.

Ngoài ra, độ cao tham số và đảo tham số thường có mối quan hệ lớn hơn với số lần giao dịch. Nếu số lần giao dịch của mô hình ít hơn, thường có thể tìm thấy một điểm tham số phù hợp, làm cho mô hình có lợi nhuận trong các giao dịch, mô hình có lợi nhuận sau khi tối ưu hóa tham số này thể hiện sự ngẫu nhiên mạnh mẽ. Nếu số lần giao dịch của mô hình nhiều hơn, sự ngẫu nhiên của mô hình sẽ giảm, thể hiện sự nhất thiết và thường xuyên của lợi nhuận, cũng sẽ có một nguyên nhân tham số cao.

• #### Phương pháp tối ưu hóa tham số

Sau khi hiểu rõ về độ cao tham số và độ cô lập tham số, phương pháp tối ưu hóa tham số trở nên quan trọng, đặc biệt là khi có nhiều tham số trong mô hình (được gọi là mảng tham số), thường thì việc lấy giá trị của một tham số sẽ ảnh hưởng đến phân bố của độ cao tham số khác. Vậy làm thế nào để tối ưu hóa mảng tham số?

Một phương pháp là phương pháp hội tụ từng bước: ưu tiên một tham số riêng lẻ, sau đó xác định giá trị tối ưu của nó, sau đó tối ưu hóa tham số khác, sau đó xác định giá trị tối ưu của nó. Như vậy, vòng lặp cho đến khi kết quả tối ưu hóa không thay đổi. Ví dụ: một mô hình giao dịch mua bán chéo thẳng hàng, hai tham số độc lập là chu kỳ ngắn trung bình N1 và chu kỳ dài N2. Đầu tiên, xác định N2 là 1, thử nghiệm lọc N1 trong phạm vi từ 1 đến 100, tìm kiếm giá trị tối ưu, cuối cùng nhận được tham số 8 và cố định; sau đó, N2 được tối ưu hóa từ 1 đến 200, được 26 và cố định; một lần nữa, N1 được tối ưu hóa vòng thứ hai, nhận được 10 tối ưu mới và cố định; cuối cùng, N2 được tối ưu hóa để có giá trị tối ưu 28 và cố định.

Một phương pháp khác là sử dụng nền tảng thiết kế phần mềm lập trình với tính toán mạnh mẽ, tính toán trực tiếp phân bố giữa hàm mục tiêu và mảng tham số, sau đó tìm phân bố đa chiều, xác định một ngưỡng chênh lệch mà giá trị tuyệt đối của chênh lệch nhỏ hơn phạm vi ngưỡng tương ứng với kích thước đa chiều lớn nhất, bán kính cắt bóng đa chiều cao nhất, được chọn là giá trị tham số ổn định nhất.

Ngoài phương pháp tối ưu hóa tham số, việc lấy mẫu dữ liệu cũng là một yếu tố quan trọng. Các mô hình theo dõi xu hướng là ý tưởng giao dịch hoạt động tốt hơn khi có xu hướng, và chiến lược mua và bán thấp là ý tưởng giao dịch hoạt động tốt hơn trong tình huống dao động. Do đó, trong tối ưu hóa tham số, cần loại bỏ một cách thích hợp các hành vi phù hợp với ý tưởng giao dịch để xem xét lợi nhuận và tăng dữ liệu về hành vi không phù hợp với ý tưởng chiến lược để xem xét tổn thất.

Ví dụ, chỉ số cổ phiếu tương lai, trong năm 2010 đầu tiên ra thị trường và cuối năm 2014 khi thị trường bò cực đoan xuất hiện, chỉ số cổ phiếu tương lai là hành động một chiều. Không có nghi ngờ gì, tất cả các mô hình xu hướng sẽ có hiệu quả tốt. Tuy nhiên, nếu chúng tôi đưa dữ liệu về tình trạng cực đoan này vào mẫu để tối ưu hóa tham số, tham số mô hình có thể không phải là tốt nhất.

Ví dụ, giả sử một mô hình có hai tham số, tham số A có kết quả kiểm tra rất tốt trong thời gian một chiều và hoạt động bình thường trong các thời gian khác; một tham số khác B có kết quả kiểm tra kém hơn tham số A trong thời gian một chiều và hoạt động tốt hơn tham số A trong các thời gian khác, phân phối giữa các thời gian khác nhau so với tham số A đều. Ngay cả khi tham số A kiểm tra các chỉ số tổng hợp như lợi nhuận rủi ro cao hơn tham số B trong toàn bộ dữ liệu mẫu, chúng ta cũng có xu hướng chọn tham số B, vì tham số B tương đối ổn định hơn và không phụ thuộc vào một mẫu cụ thể.

Tóm lại, trong việc xây dựng mô hình giao dịch theo quy trình, một mặt, có thể cải thiện mô hình thông qua tối ưu hóa tham số để mô hình thích ứng tốt hơn với mô hình biến động giá, tăng lợi nhuận đầu tư; mặt khác, cần ngăn chặn việc phù hợp quá mức với tối ưu hóa tham số, dẫn đến việc giảm đáng kể khả năng thích ứng của mô hình với sự thay đổi của thị trường.

Tải về từ Programmable Trader