Toán học và cờ bạc

• Chúng ta biết cờ bạc là một trò chơi xác suất, và đó là một số kết quả cờ bạc kỳ lạ đã thu hút sự quan tâm của nhà toán học Pascal và nhà toán học vĩ đại Fermat, họ đã trao đổi qua thư, đưa ra một số nguyên tắc về lý thuyết xác suất, do đó tạo ra lý thuyết xác suất.

• 1. Cờ bạc hoàn hảo

Đội NBA Lakers và Cowboys có một trận đấu, và cả hai đội đều có những người hâm mộ trung thành, hãy gọi họ là những người hâm mộ người dân tộc người Hồng Kông và những người hâm mộ người Hồng Kông. Tất nhiên người hâm mộ cảm thấy rằng đội mà họ ủng hộ có nhiều khả năng thắng hơn, vì vậy họ sẵn sàng đặt cược với bạn. Giả sử người hâm mộ người Hồng Kông nghĩ rằng tỷ lệ thắng của Lakers là p, người hâm mộ người Hồng Kông nghĩ rằng tỷ lệ thắng của Hồng Kông là q, p và q đều phải lớn hơn 50%.

Cách thức này là: chúng ta đặt cược tương tự như các con chuột của người Lhasa và các con bò của người Lhasa, nếu chúng ta thắng, chúng ta sẽ nhận được y đồng, nếu thua, chúng ta sẽ mất x đồng, miễn là y>x chúng ta sẽ thắng. Và x và y chỉ cần đáp ứng hai phương trình đơn giản sau đây, lợi nhuận kỳ vọng của các con chuột của người Lhasa và các con bò của người Lhasa là dương, chúng ta sẽ đặt cược với chúng ta:

```
p * x - ( 1-p ) * y > 0
q * x - ( 1-q ) * y > 0
```

Với giới hạn y>x, hình ảnh được vẽ là khu vực được bao quanh bởi ba đường thẳng, và giá trị tọa độ của bất kỳ điểm nào trong đó (x, y) là một giải pháp nhất định. Nếu p>q, giải pháp là phần màu xanh trong biểu đồ sau:

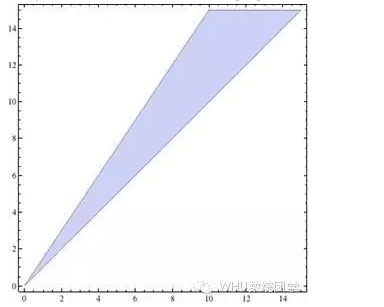
Vấn đề này có vẻ đã được giải quyết hoàn hảo, nhưng có một vấn đề nữa, và tôi tin rằng người đọc sẽ sớm nhận ra sự vô lý của nó: cho dù là những con chó con người hay những con chó con bò, họ đều có kỳ vọng về lợi nhuận tích cực, nghĩa là, về lâu dài, họ sẽ kiếm tiền, trong khi chúng ta vẫn ổn định và không thua lỗ, vậy thì tiền từ đâu đến, và làm thế nào mọi người có thể kiếm được tiền?

• ### Lừa đảo 2 và 3 thẻ

Đây là một trò đùa khéo léo khác, chúng ta chuẩn bị ba lá bài, lá bài số 1 đối diện là đen, lá bài số 2 đối diện là đỏ, lá bài số 3 một mặt là đen, một mặt là đỏ. Sau đó đặt các lá bài vào một hộp, lắc lắc, để đối thủ rút một tấm phẳng lên bàn.

Thực tế, chúng ta có cơ hội thắng không phải là ¹⁄₂, mà là ²⁄₃, và điều khó hiểu nhất trong trò chơi này là tính hai mặt của các lá bài. Người chơi rút không phải là 3 lá bài, mà là 6 lá bài: 3 lá đen, 3 lá đỏ. Chúng ta đánh số 6 lá bài này là A, B, C, D, E, F:

Khi người chơi rút ra mặt đen, đó là ba trường hợp có thể xảy ra, A, C, D, và mặt sau của chúng là D, F, A, với màu đen chiếm ²⁄₃ .

Vấn đề này được đưa ra lần đầu tiên vào năm 1889 bởi nhà toán học người Pháp Joseph Louis François Bertrand, và vì kết quả của vấn đề này là bất ngờ, nó được gọi là nghịch lý hộp Bertrand. Năm 1950, nhà toán học người Mỹ Warren Weaver đã giới thiệu cách chơi bài ở trên, mà Martin Gardner gọi là lừa đảo ba thẻ.

• ### 3, Một loại hạt anh đào rất khác thường

Đôi khi chúng ta bắt đầu đánh bạc bằng cách để người khác kiếm một ít tiền, rồi sau đó đánh hết lưới. Dưới đây là một ví dụ tuyệt vời. Bốn người đang chơi bài cầu, tôi nói: Hãy đánh một con cá, tôi có một A, bạn đoán xem tôi có thêm A không? Trong trường hợp này, bạn có thể sẽ thua, và khi đó bạn trong tâm trí chỉ định một màu A, ví dụ như A củ cải, và khi một vòng bắt được A củ cải, thì cơ hội sẽ đến: Hãy đánh một con cá nữa, tôi có một con cá A, bạn đoán xem tôi có thêm A củ cải không?

Nhiều người chắc chắn sẽ nghĩ rằng hai con ếch không có gì khác nhau, thêm vào đó là một quả anh đào và không có vấn đề gì. Nhưng sự khác biệt giữa chúng là quá lớn đến nỗi không thể tin được.

  没有A的情形：C（48，13）
  至少有1张A的情形：C（52，13）－C（48，13）
  恰好有1张A的情形：4＊C（48，12）
  至少有2张A的情形：C（52，13）－C（48，13）－4＊C（48，12）
  事件X为至少有两张A，事件Y为至少有一张A，那么条件概率为：

  P（X｜Y）＝P（XY）／P（Y）=(C（52，13）－C（48，13）－4＊C（48，12）)/(C（52，13）－C（48，13）)≈37%

Lúc này tôi muốn tự đặt cược cho mình là A, dễ dàng để thua hơn. Nhưng sau khi đặt cược lần đầu tiên, mọi người đã quyết định đặt cược, một khi người chơi thứ hai thay đổi quần áo, họ đã đặt cược nhiều hơn, sau đó tôi không có thêm A, ngay giữa chúng tôi.

  有黑桃A的情形：C（51，12）
  没有其它A的情形：C（48，12）
  还有其它A的情形：C（51，12）－C（48，12）
  事件X为还有其它A，事件Y为有黑桃A，条件概率为：

  P（X｜Y）＝P（XY）／P（Y）＝（C（51，12）－C（48，12））／C（51，12）≈56%。

Tác giả: WHU Statistics